[자료구조 및 알고리즘] BST(Binary Search Tree) (C++)

신동욱·2024년 12월 30일

자료구조 및 알고리즘

목록 보기

11/18

1. 정의

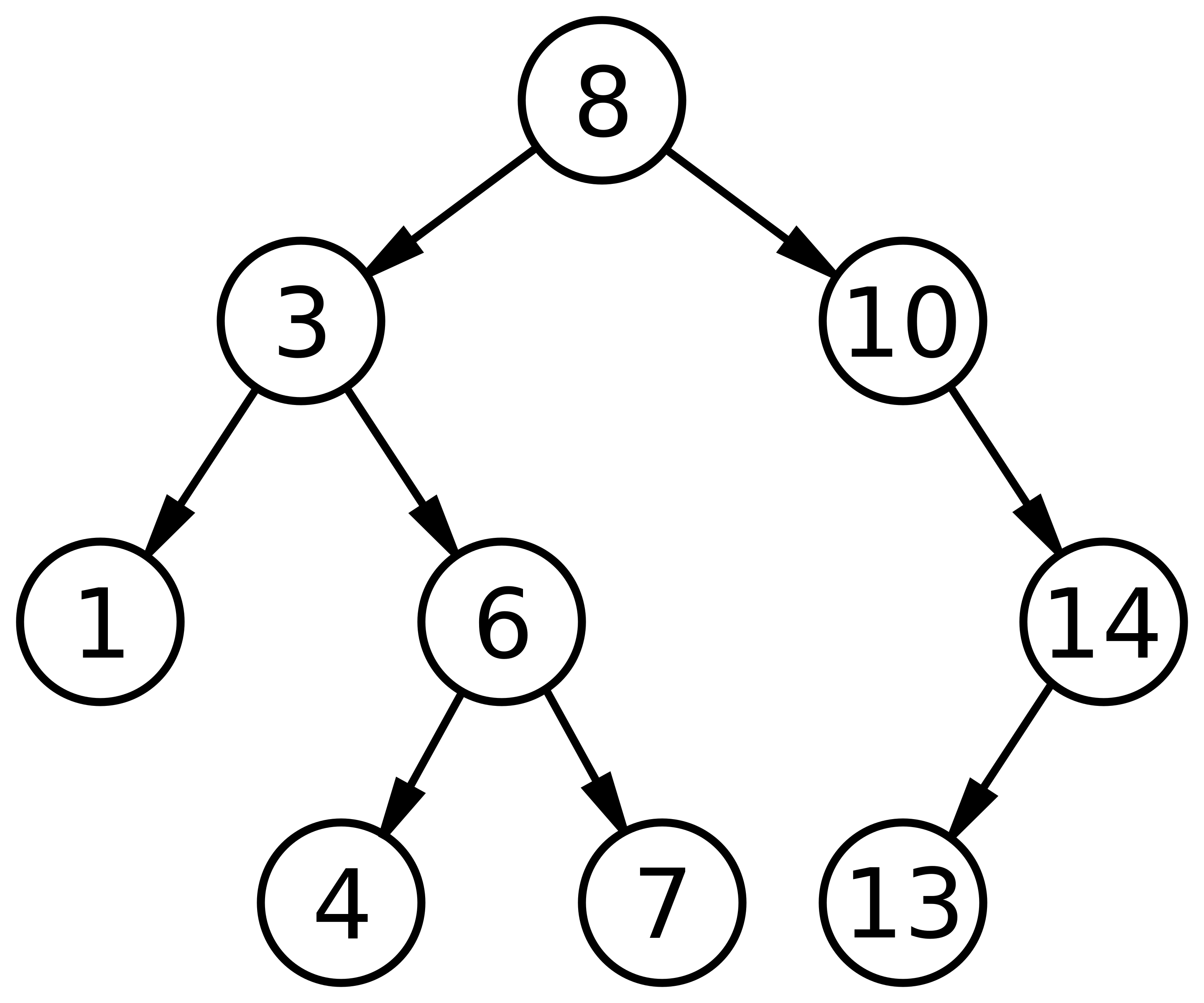
이진 탐색 트리(BST, Binary Search Tree)는 bst property를 만족하는 트리 자료구조입니다.

bst property란?
왼쪽 서브트리(sub tree)의 키 값 < 노드의 키 값 < 오른쪽 서브 트리(sub tree)의 키 값

2. 이진 탐색 트리의 ADT(Abstract Data Type)와 구현

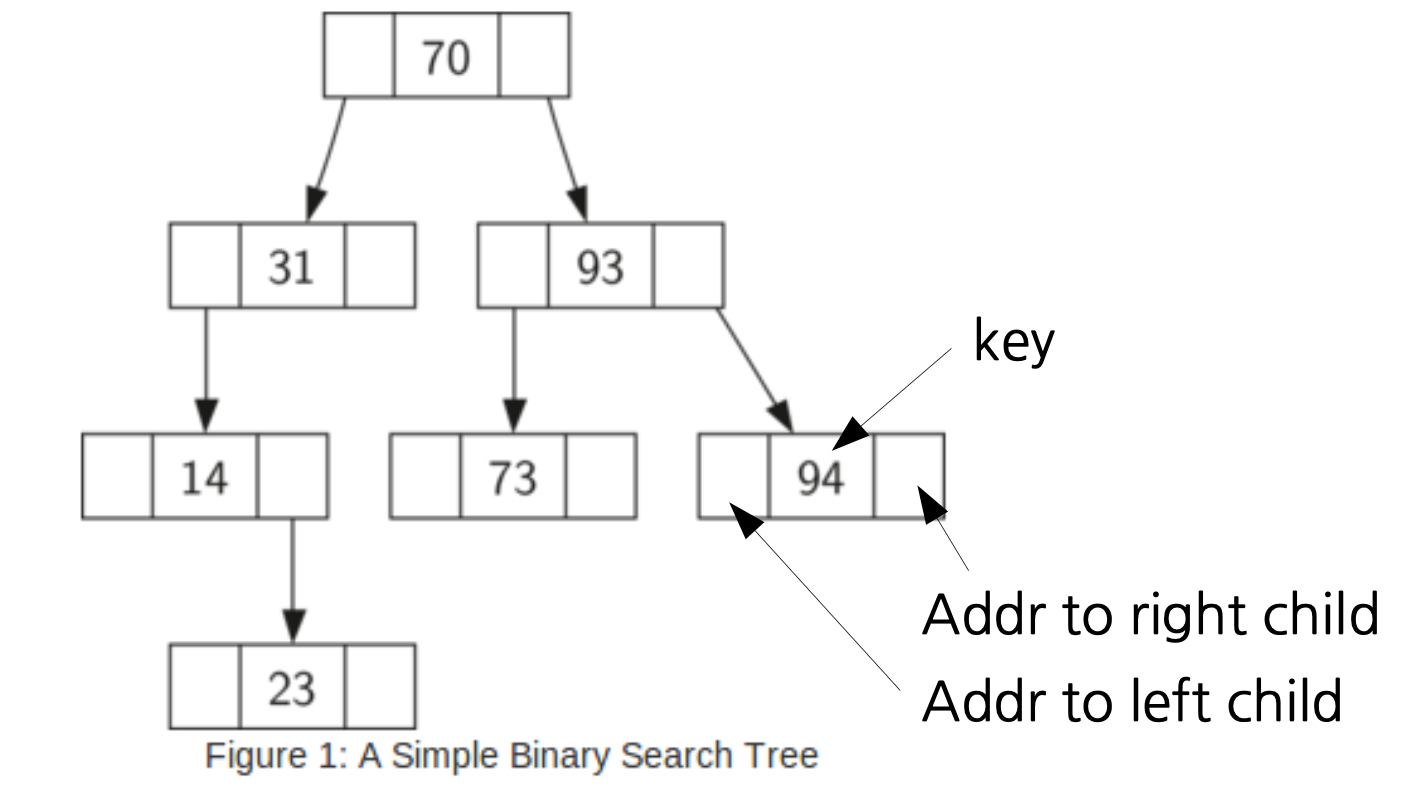
📦 데이터

key : 비교 연산을 수행하기 위해 사용하는 값 (중복되지 않아야 함)
value : 키와 연관된 데이터 (필수는 아님)
left : 왼쪽 자식 노드
right : 오른쪽 자식 노드

따라서 다음과 같이 트리의 노드를 나타내는 구조체를 선언할 수 있습니다.

struct TreeNode
{
    int key;
    string value;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int k, string v)
    {
        key = k;
        value = v;
        left = nullptr;
        right = nullptr;
    }
};

참고로 구조체도 클래스와 같이 생성자를 둘 수 있습니다.

⚙️ 연산

1. 삽입(Insert)

새로운 키가 부모 노드의 키보다 작으면 왼쪽 서브트리로 삽입
새로운 키가 부모 노드의 키보다 크면 오른쪽 서브트리로 삽입

트리 구조는 재귀적으로 서브트리에 접근하면 됩니다. 삽입하려는 키 값이 bst property를 만족하도록 노드를 이동합니다.

void Insert(TreeNode* cur, int key, string value)
{
    // 왼쪽
    if (key < cur->key)
    {
        if (cur->left == nullptr)
            cur->left = new TreeNode(key, value);
        else
            Insert(cur->left, key, value);
    }
    // 오른쪽
    else
    {
        if (cur->right == nullptr)
            cur->right = new TreeNode(key, value);
        else
            Insert(cur->right, key, value);
    }
}

2. 탐색(Search)

현재 노드의 키와 탐색 키를 비교
탐색 키가 현재 노드의 키보다 작으면 왼쪽 서브트리 탐색
탐색 키가 현재 노드의 키보다 크면 오른쪽 서브트리 탐색

삽입 연산과 크게 다르지 않습니다. 이진 탐색을 하는 것처럼 노드를 이동합니다.

void Search(TreeNode* cur, int key)
{
    if (key < cur->key)
    {
        if (cur->left == nullptr)
            cout << "tree hasn't key : " << key << '\n';
        else
            Search(cur->left, key);
    }
    else if (key > cur->key)
    {
        if (cur->right == nullptr)
            cout << "tree hasn't key : " << key << '\n';
        else
            Search(cur->right, key);
    }
    else
        cout << "value : " << cur->value << '\n';
}

3. 삭제(Delete)
삭제 연산은 노드를 삭제하고 서브 트리를 루트에 연결하는 작업이 필요합니다. 이때 노드를 삭제하는 세 가지 케이스가 있습니다.

Case1 : 삭제할 노드가 리프 노드(자식이 없는 경우)

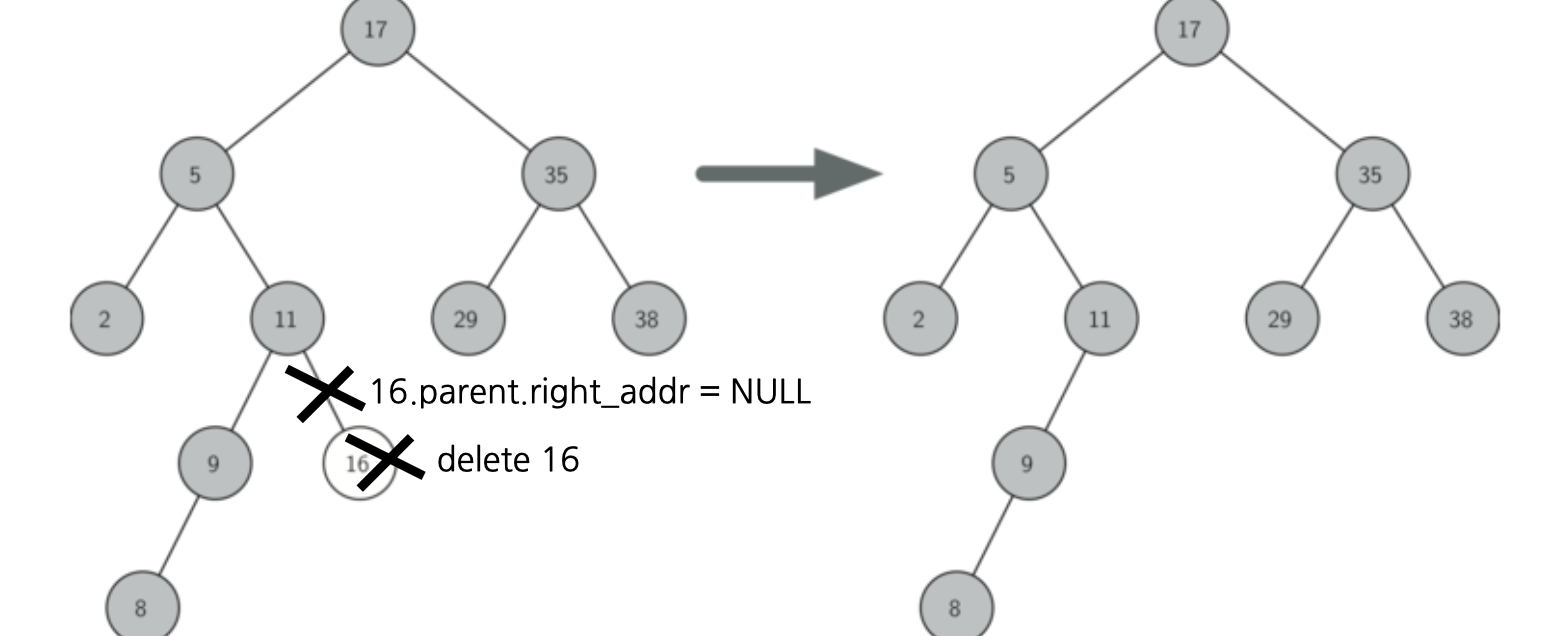
삭제하려는 노드를 delete(메모리 반납)하고, 해당 엣지(Edge)를 널(nullptr)로 초기화 합니다.

if (cur->left == nullptr && cur->right == nullptr)
{
	// case1 : deletion of a node without children
	// 그냥 삭제
	delete cur;
	return nullptr;
}

Case2 : 삭제할 노드가 자식 노드 하나만 있는 경우

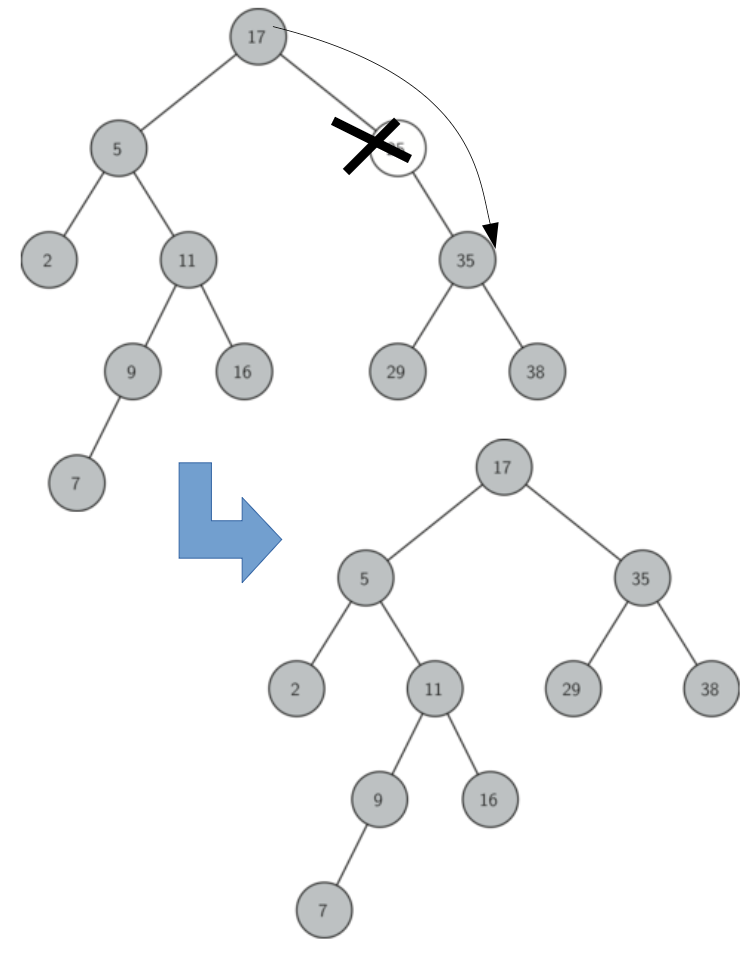
자식 노드를 현재 노드의 위치로 변경합니다. 위 그림에서는 17의 right가 35를 가리키도록 재귀를 타고 목표 노드로 간 다음 35의 주소를 리턴합니다.

else if (cur->right == nullptr)
{
	// case2 : deletion of a node with one child
	// 왼쪽만 있는 경우
	// 왼쪽을 부모 노드에 잇는다
	TreeNode* tmp = cur->left;
	delete cur;
	return tmp;
}
else if (cur->left == nullptr)
{
	// case2 : deletion of a node with one child
	// 오른쪽만 있는 경우
	// 오른쪽을 부모 노드에 잇는다
	TreeNode* tmp = cur->right;
	delete cur;
	return tmp;
}

Case3 : 삭제할 노드가 자식 노드 두 개가 있는 경우

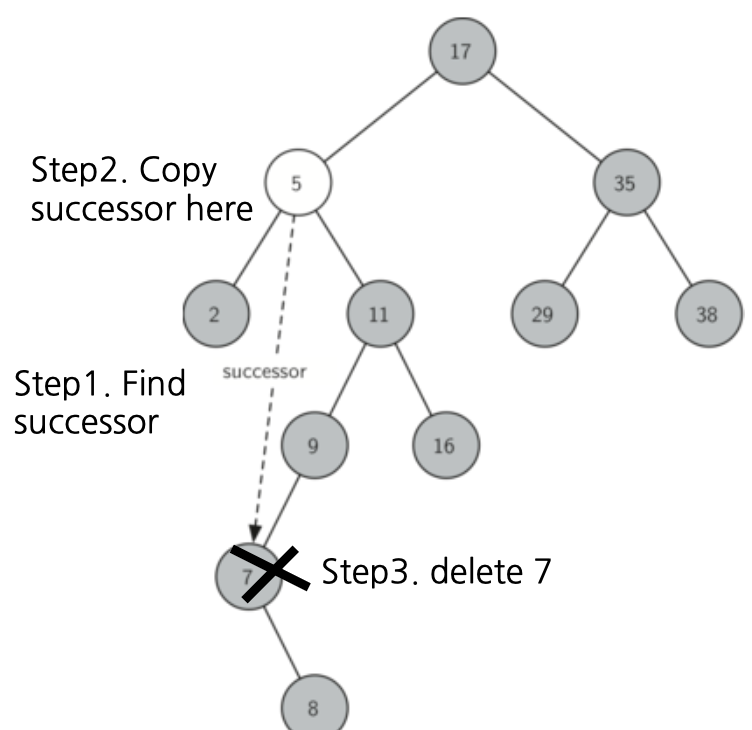
Step1. 후속자(Successor)를 찾습니다.
여기서 후속자는 오른쪽 서브트리에서 키 값이 가장 작은 노드입니다. 후속자는 키 값이 현재 노드의 left보다는 크고, right보다는 작은데, 항상 자식이 하나이거나 없습니다. 때문에 case1이나 case2의 프로세스대로 삭제를 수행할 수 있습니다.

Step2. 후속자의 key와 value를 삭제하고자 하는 노드로 복사합니다.

Step3. 후속자를 삭제합니다.
이 과정은 case1 또는 case2의 과정으로 완료될 수 있습니다.

else
{
	// case3 : deletion of a node with two children
	// Step1. Find the successor(Successor has one or no child)
	// The minimal key node on the right subtree of the node to delete
	// (or the maximal key node on the left subtree of the node to delete)
	TreeNode* tmp = FindMin(cur->right);

	// Step2. Copy of successor to the node to delete
	cur->key = tmp->key; cur->value = tmp->value;
	// Step3. Delete the successor
	// This process can be done by deletion of case
	cur->right = Delete(cur->right, tmp->key);
}

4. 최소값(Find Minimum)
트리에서 가장 작은 키를 가진 노드를 찾습니다. 왼쪽 자식이 없을 때, 해당 노드가 최소값입니다.

TreeNode* FindMin(TreeNode* root)
{
    while (root->left != nullptr)
        root = root->left;
    return root;
}

5. 최대값(Find Maximum)
트리에서 가장 큰 키를 가진 노드를 찾습니다. 오른쪽 자식이 없을 때, 해당 노드가 최대값입니다.

TreeNode* FindMax(TreeNode* root)
{
    while (root->right != nullptr)
        root = root->right;
    return root;
}

6. 중위 순회(Inorder Traversal)
트리를 중위 순회하여 정렬된 키를 반환합니다.

왼쪽 서브트리 -> 현재 노드 -> 오른쪽 서브트리

void Inorder(TreeNode* root)
{
    Inorder(root->left);
    cout << "key : " << root->key << " value : " << root->value << '\n';
    Inorder(root->right);
}

7. 높이 (Height)
트리의 높이를 반환합니다.

루트 노드에서 가장 깊은 리프 노드까지의 경로 길이를 반환


int getHeight(TreeNode* root)
{
    if (root == nullptr)
        return 0;

    int leftSubTreeheight = getHeight(root->left);
    int rightSubTreeheight = getHeight(root->right);

    return max(leftSubTreeheight, rightSubTreeheight) + 1;
}

8. 노드 개수 계산 (Count Nodes)
트리의 총 노드 개수를 반환합니다.

int getLen(TreeNode* root)
{
    if (root == nullptr)
        return 0;

    int leftSubTreeLen = getLen(root->left);
    int rightSubTreeLen = getLen(root->right);

    return leftSubTreeLen + rightSubTreeLen + 1;
}

3. BST 복잡도 분석

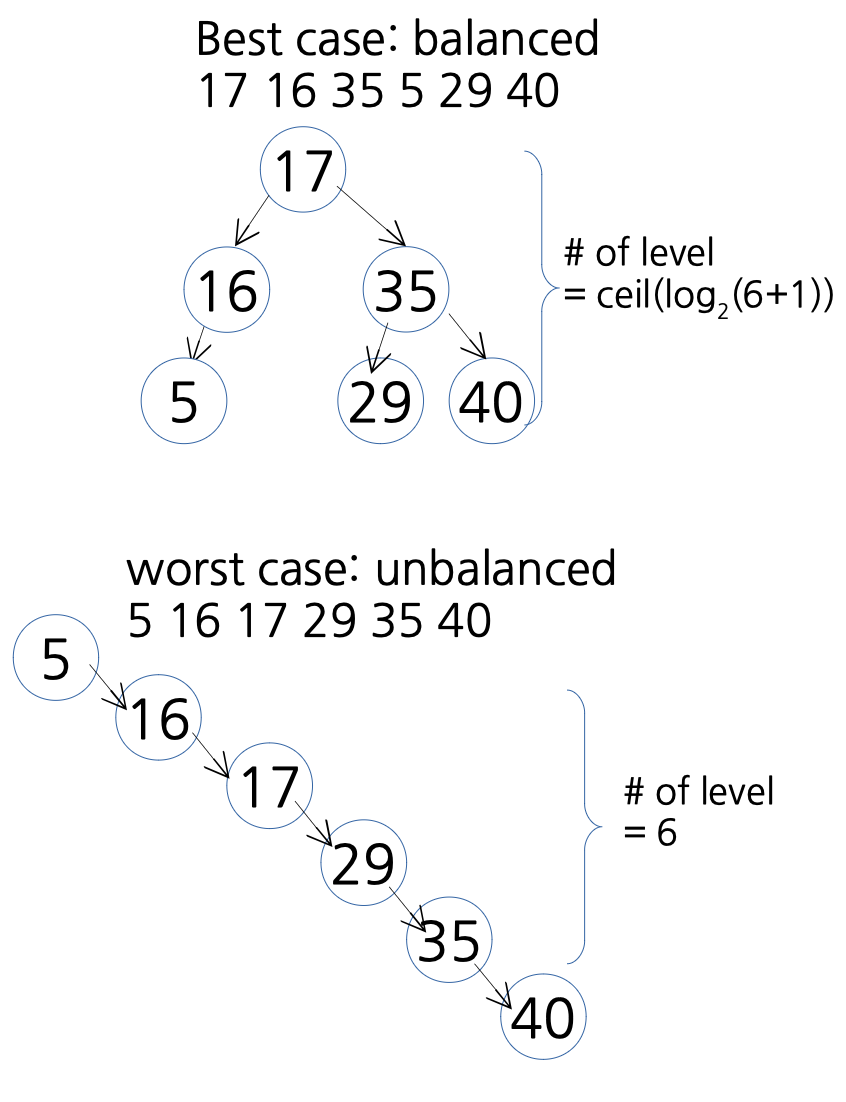
삽입(Insertion)의 복잡도 : $O(N)$

Best : $log N$
Wort : $N$

탐색(Search)의 복잡도 : $O(N)$

Best : $log N$
Wort : $N$

삭제(Deletion)의 복잡도 : $O(N)$

Best : $log N$
Wort : $N$

$O(N)$ 의 시간복잡도로는 트리 자료구조를 사용하는데 이득이 없습니다. 시간복잡도를 $O(logN)$ 으로 줄이기 위해, 균형 이진 탐색 트리(Balanced Binary Search Tree)가 존재합니다. 이는 다음 시간에 다뤄보도록 하겠습니다.

4. 전체 코드 및 테스트 코드

#include <iostream>
#include <string>
using namespace std;

struct TreeNode
{
    int key;
    string value;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int k, string v)
    {
        key = k;
        value = v;
        left = nullptr;
        right = nullptr;
    }
};

void Insert(TreeNode* cur, int key, string value)
{
    // 왼쪽
    if (key < cur->key)
    {
        if (cur->left == nullptr)
            cur->left = new TreeNode(key, value);
        else
            Insert(cur->left, key, value);
    }
    // 오른쪽
    else
    {
        if (cur->right == nullptr)
            cur->right = new TreeNode(key, value);
        else
            Insert(cur->right, key, value);
    }
}

void Search(TreeNode* cur, int key)
{
    if (key < cur->key)
    {
        if (cur->left == nullptr)
            cout << "tree hasn't key : " << key << '\n';
        else
            Search(cur->left, key);
    }
    else if (key > cur->key)
    {
        if (cur->right == nullptr)
            cout << "tree hasn't key : " << key << '\n';
        else
            Search(cur->right, key);
    }
    else
        cout << "value : " << cur->value << '\n';
}

TreeNode* FindMin(TreeNode* root)
{
    while (root->left != nullptr)
        root = root->left;
    return root;
}

TreeNode* FindMax(TreeNode* root)
{
    while (root->right != nullptr)
        root = root->right;
    return root;
}

TreeNode* Delete(TreeNode* cur, int key)
{
    if (cur == nullptr) {
        cout << "tree hasn't key : " << key << '\n';
        return cur;
    }


    if (key < cur->key)
        cur->left = Delete(cur->left, key);
    else if (key > cur->key)
        cur->right = Delete(cur->right, key);
    else
    {
        if (cur->left == nullptr && cur->right == nullptr)
        {
            // case1 : deletion of a node without children
            // 그냥 삭제
            delete cur;
            return nullptr;
        }
        else if (cur->right == nullptr)
        {
            // case2 : deletion of a node with one child
            // 왼쪽만 있는 경우
            // 왼쪽을 부모 노드에 잇는다
            TreeNode* tmp = cur->left;
            delete cur;
            return tmp;
        }
        else if (cur->left == nullptr)
        {
            // case2 : deletion of a node with one child
            // 오른쪽만 있는 경우
            // 오른쪽을 부모 노드에 잇는다
            TreeNode* tmp = cur->right;
            delete cur;
            return tmp;
        }
        else
        {
            // case3 : deletion of a node with two children
            // Step1. Find the successor(Successor has one or no child)
            // The minimal key node on the right subtree of the node to delete
            // (or the maximal key node on the left subtree of the node to delete)
            TreeNode* tmp = FindMin(cur->right);

            // Step2. Copy of successor to the node to delete
            cur->key = tmp->key; cur->value = tmp->value;
            // Step3. Delete the successor
            // This process can be done by deletion of case
            cur->right = Delete(cur->right, tmp->key);

        }
    }

    return cur;
}

void Inorder(TreeNode* root)
{
    Inorder(root->left);
    cout << "key : " << root->key << " value : " << root->value << '\n';
    Inorder(root->right);
}

int getHeight(TreeNode* root)
{
    if (root == nullptr)
        return 0;

    int leftSubTreeheight = getHeight(root->left);
    int rightSubTreeheight = getHeight(root->right);

    return max(leftSubTreeheight, rightSubTreeheight) + 1;
}

int getLen(TreeNode* root)
{
    if (root == nullptr)
        return 0;

    int leftSubTreeLen = getLen(root->left);
    int rightSubTreeLen = getLen(root->right);

    return leftSubTreeLen + rightSubTreeLen + 1;
}

int main()
{
    TreeNode* root = new TreeNode(8, "root");

    Insert(root, 3, "뭘");
    Insert(root, 10, "적을까");
    Insert(root, 1, "뭐적지");
    Insert(root, 6, "귀찮노");
    Insert(root, 14, "음음");
    Insert(root, 4, "아무거나");
    Insert(root, 7, "뭐징");
    Insert(root, 13, "ㅋㅋ");

    Search(root, 13);

    int len = getLen(root);
    cout << "tree의 길이 : " << len << '\n';
    int height = getHeight(root);
    cout << "tree의 높이 : " << height << '\n';

    Delete(root, 4);
    len = getLen(root);
    cout << "tree의 길이 : " << len << '\n';
    height = getHeight(root);
    cout << "tree의 높이 : " << height << '\n';

    Delete(root, 7);
    len = getLen(root);
    cout << "tree의 길이 : " << len << '\n';
    height = getHeight(root);
    cout << "tree의 높이 : " << height << '\n';

    Delete(root, 13);
    len = getLen(root);
    cout << "tree의 길이 : " << len << '\n';
    height = getHeight(root);
    cout << "tree의 높이 : " << height << '\n';

    return 0;
}

신동욱

이전 포스트

[자료구조 및 알고리즘] Tree (C++)

다음 포스트

[자료구조 및 알고리즘] BST(Binary Search Tree) (C++)