개요
그래프에서 최단 거리를 구할 때 사용되는 다익스트라, 벨만-포드, 플로이드-워셜 그 중 다익스트라(Dijkstra) 알고리즘에 관하여 알아봅시다.
다익스트라 알고리즘은 앞서 말했듯이 그래프에서 한 정점에서 다른 정점까지의 최단 거리를 구하는 알고리즘입니다. 다익스트라에서는 매번 최단 거리를 선택하여 탐색을 진행하는 그리디 형식으로 진행됩니다.
다익스트라 알고리즘에서는 그래프의 어느 간선의 가중치라도 음수가 존재하면 안됩니다.
진행 과정
다익스트라는 다음과 같은 과정으로 진행됩니다.
- 시작점을 설정한다.
- 최단 거리를 저장할 배열을 초기화한다.
- 방문하지 않은 정점 중 가장 가중치가 작은 정점을 선택한다. (처음에는 시작 정점 방문)
- 해당 정점을 거쳐 다른 정점으로 이동하는 거리가 이전에 기록한 거리보다 작다면 거리를 갱신한다.
- 모든 정점을 탐색할 때 까지
3~4과정을 반복한다.
아래 예시를 보며 이해해봅시다.
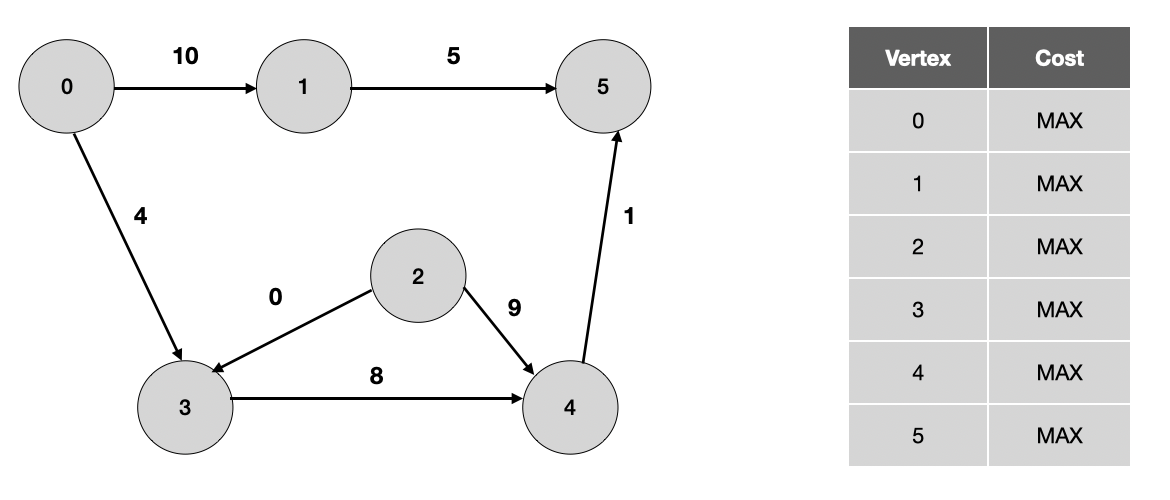
위와 같은 그래프가 있다고 할 때, 다익스트라를 진행하기 위하여 최단 거리를 저장할 배열을 모두 MAX값으로 설정합니다.
일반적으로 MAX값은 INT_MAX로 설정해도 되지만, int범위보다 큰 값을 사용한다면 더 큰 값을 MAX값으로 설정해야 합니다.
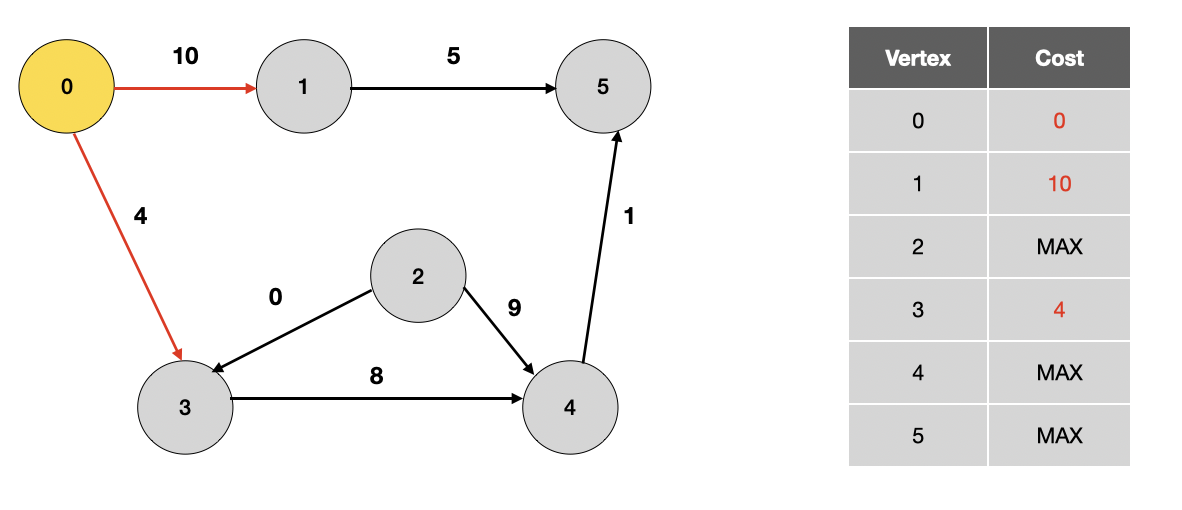
가장 먼저 시작 정점을 방문하여 시작 정점에서 방문할 수 있는 정점들에 대한 거리를 갱신합니다.
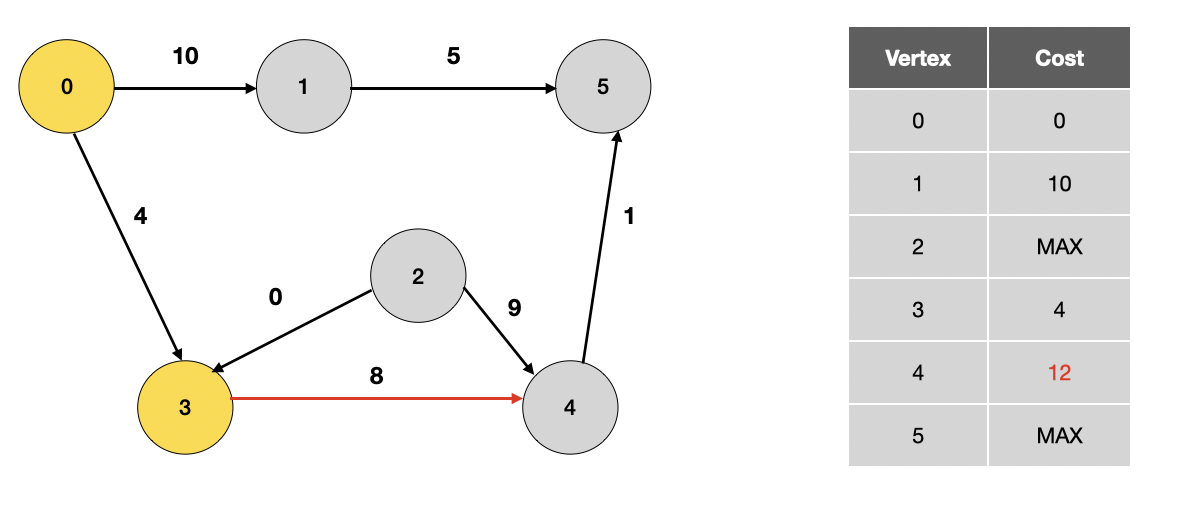
방문하지 않은 정점 중 가장 가중치가 작은 3번 정점을 방문합니다.
0번 정점에서 3번 정점을 거쳐 4번 정점으로 이동하면 최단 거리이므로 거리를 갱신합니다. (MAX > 12)
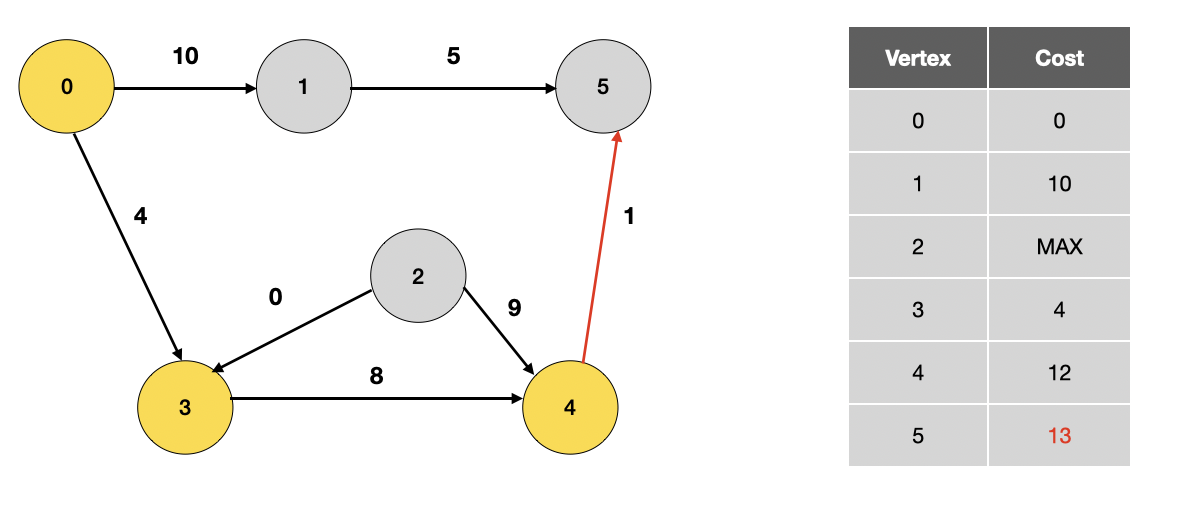
방문하지 않은 정점 중 가장 가중치가 작은 4번 정점을 방문합니다.
0번 정점 -> 3번 정점 -> 4번 정점을 거쳐 5번 정점으로 이동하면 최단 거리이므로 거리를 갱신합니다. (MAX > 13)
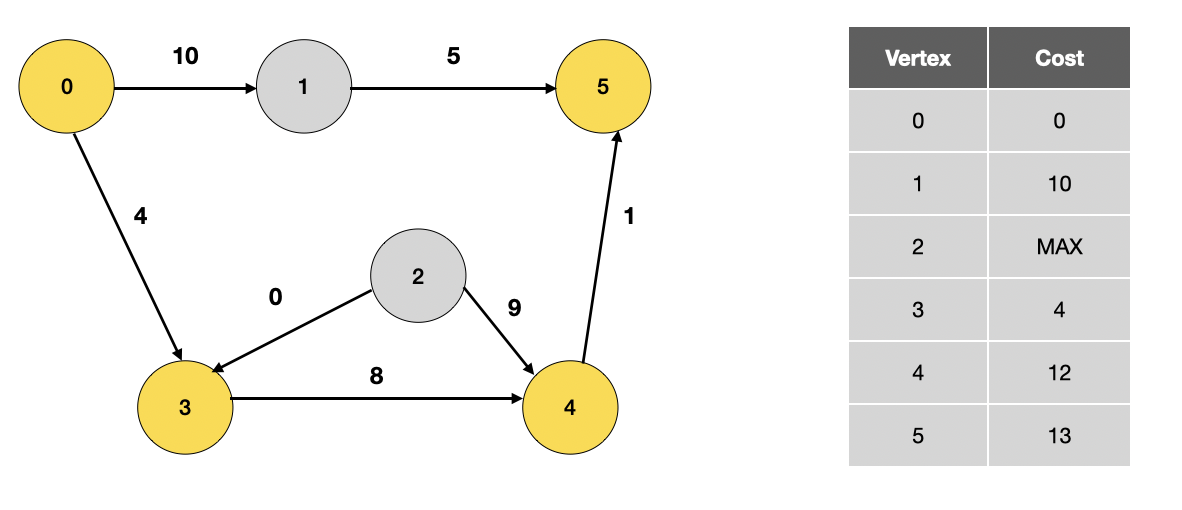
방문하지 않은 정점 중 가장 가중치가 작은 5번 정점을 방문합니다.
갱신할 거리가 없기 때문에 아무것도 갱신하지 않습니다.
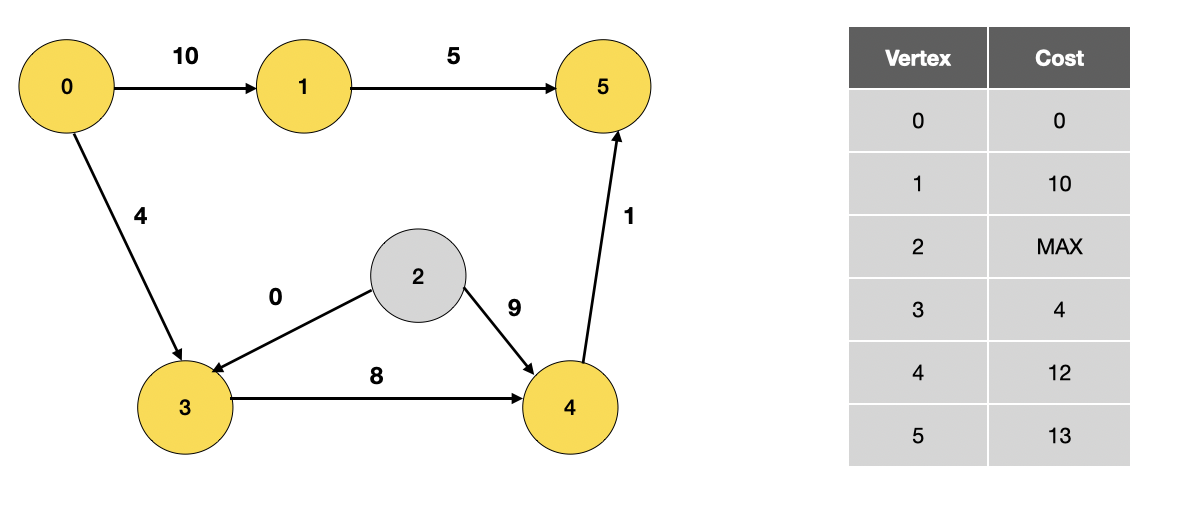
방문하지 않은 정점 중 가장 가중치가 작은 1번 정점을 방문합니다.
0번 정점 -> 1번 정점을 거쳐 5번 정점으로 이동할 수 있지만, 최단 거리가 아니므로 거리를 갱신하지 않습니다.
모든 정점을 방문했으므로 탐색이 종료됩니다. 탐색이 종료된 후 배열 속 Cost값이 시작 정점에서 각 정점으로 이동할 때에 최단 거리입니다. 탐색 종료 시점에서 거리가 MAX인 정점이 존재한다면 해당 정점은 시작점에서 이동 불가한 정점입니다.
C++ 코드 구현
다익스트라 알고리즘을 구현하는 방법은 배열을 이용할 수도 있고, 우선순위 큐를 사용할 수도 있습니다.
정점의 갯수를 V라 하고 간선의 갯수를 E라고 할 때 배열을 이용하는 구현방식은 O(V^2)의 시간복잡도를 가지고, 우선순위 큐를 이용하는 방식은 O(E log V)의 시간복잡도를 가집니다.
이 글에서는 더욱 간단하고 빠른 우선순위 큐를 이용하여 다익스트라를 구현 해보겠습니다.
vector<int> dijkstra(int start){
// 2번 과정. 최단 거리를 저장할 배열을 모두 MAX값으로 초기화 시켜준다.
vector<int> dist(V, INT_MAX);
// 방문하지 않은 정점을 담을 우선순위 큐
// 방문하지 않은 정점 중 가장 가중치가 작은 정점을 선택해야 하므로 오름차순으로 정렬한다.
// 가중치가 정렬에 기준이 되어야 하므로 pair에 first에는 가중치, second에는 정점이 들어간다.
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>> pq;
// 시작 정점 방문체크
dist[start] = 0;
pq.push({ 0, start });
while(!pq.empty()){
// 3번 과정. 방문하지 않은 정점 중 가장 가중치가 작은 정점 선택
pair<int, int> cur = pq.top();
pq.pop();
for(int i = 0; i < graph[cur.second].size(); i++){
pair<int ,int> next = graph[cur.second][i];
// 4번 과정 최단 거리라면 거리를 갱신해주기
if(cur.first + next.second < dist[next.first]){
dist[next.first] = cur.fisrt + next.second;
// 우선순위 큐에 담아주기
pq.push(next);
}
}
}
// 모든 정점의 탐색이 끝난 후 완성된 최단 거리 배열을 리턴한다.
return dist;
}