[백준 1167] 트리의 지름

🔗알고리즘 문제

보자마자 아 DFS문제!! 라는 생각이 들었다. DFS로 해결하였지만.. 시간초과를 해결하기 위한 발상을 해내기가 조금 힘든 문제였다.

문제 분석

이 문제는 트리의 지름을 출력하는 문제이다.

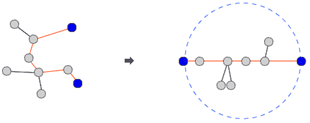
어떤 트리에서 거리가 가장 먼 두 노드를 양쪽으로 쫙 잡아당기면, 그 외의 노드들은 모두 이 두 노드를 지름의 끝 점으로 하는 원안에 들어가게 된다.

이 때 두 노드의 거리를 트리의 지름이라고 부른다고 한다.

알기 쉽게 정의하자면 트리의 지름은 트리에서 가장 거리가 먼 두 점 사이의 거리이다.

따라서 이 문제는 트리의 정보가 주어질 때 트리의 지름을 구하면 되는 문제이다.

발상

이 문제에 입력에서는 각 노드와 연결되어 있는 노드와 가중치가 주어진다. 이에 따라 각 노드마다 DFS를 진행하여 가장 거리가 멀 때에 거리를 출력해야겠다고 생각하였다.

이러한 방식은 각 노드마다 DFS를 진행해야하기에 O(n^2)의 시간복잡도를 가진다. 하지만 이 문제에서 들어오는 정점의 갯수는 총 100,000개로 이런 방식으로 해결하였다가는 시간초과를 해결할 수 없을 것이라 생각하였다...

도저히 다른 방법이 생각나지 않아 트리의 지름 이론을 찾아보게 되었다. 여러 내용이 있지만 결국 정리하면..

1. 트리에서 임의의 노드 u를 잡고 u에서 가장 먼 노드 v를 찾는다.
2. v에서 가장 먼 노드인 k를 찾는다.
3. 이 때 트리의 정점은 v와 k 사이의 거리이다.

트리의 정점을 굳이 모든 정점을 탐색하지 않아도 찾을 수 있다는 사실을 깨달았다.

알고리즘 설계

1. 트리의 정보를 입력받는다.
2. 시작점을 1로 잡고 DFS를 진행한다.
3. 찾아온 가장 먼 노드를 시작점으로 하여 다시 DFS를 진행한다.
4. 트리의 지름을 출력한다.

코드

#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

vector<pair<int, int>> v[100001] = {};
bool check[100001] = {};

int start = 0;
int answer = 0;

void dfs(int node, int dis){
    check[node] = true;

    if(answer < dis){
        answer = dis;
        start = node;
    }

    for(auto & i : v[node]){
        if(check[i.first])
            continue;

        dfs(i.first, dis + i.second);
    }
}

int main(){
    int n = 0;

    cin >> n;

    for(int i = 0; i < n; i++){
        int vertex;
        cin >> vertex;

        while(true){
            int next;
            int dis;

            cin >> next;
            if(next == -1)
                break;
            cin >> dis;

            v[vertex].emplace_back( next, dis );
        }
    }

    dfs(1, 0);
    answer = 0;
    memset(check, false, sizeof(check));
    dfs(start, 0);

    cout << answer;
}

참고

https://velog.io/@zioo/트리의-지름-구하기