[백준 1185] 유럽여행

🔗 알고리즘 문제

가중치의 값을 잘 생각해야하는 MST문제이다. 아직 MST가 익숙하지 않아 꽤나 고난을 겪었지만, 그래도 잘 해결해서 뿌듯하다.

문제 분석

이 문제는 각 나라에 방문할 때 내야하는 비용과 도로를 이동할 때 드는 비용이 주어질 때, 최소 금액으로 각 나라를 모두 한번씩 돌고 시작 나라로 돌아오도록 하는 문제이다.

발상 & 알고리즘 분석

문제를 읽어보면 최대한 많은 길을 제거하여 최소의 길만 남긴다는 것을 보며 해당 문제가 MST문제라는 것을 짐작할 수 있다.

하지만, 그냥 MST와는 다르게 가중치의 값을 변형해서 주어야 하는데, 그 이유는 도로를 지나갈 때가 아닌 나라에 방문했을 때도 비용을 지불해야하기 때문이다.

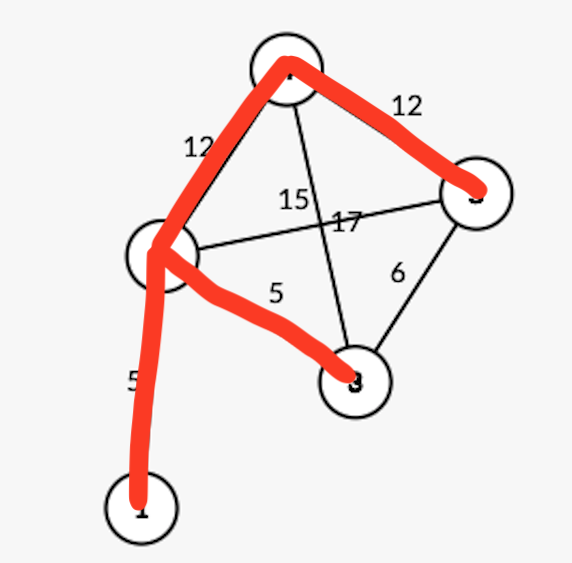
1번 문제의 그래프를 보면 최소비용을 구하기 위해서 빨간 선의 MST가 나오게 된다. 하지만 여기서 가중치를 도로에만 적용한다면 3-5 도로의 6가중치를 놔두고 12가중치를 선택할 이유가 전혀 없다.

따라서 가중치의 값을 변형하여 MST를 구해야한다.

이제 스패닝 트리에서 시작지점에서 출발하여 시작지점으로 돌아오려면 어떤 경로가 나오는지 살펴보면 가중치를 알 수 있는데, 모든 도로를 각각 2번씩 방문하는 것을 알 수 있다.

따라서 x, y의 가중치는 도로의 가중치 * 2 + x나라의 비용 + y나라의 비용이다.

시작지점으로 다시 돌아오게 되므로 최소 비용을 가진 나라의 비용을 한번 더해주어 최종 비용을 얻을 수 있다.

코드

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

struct Edge{
    int from;
    int to;
    int val;
};

int parents[10001] = {};
int vals[10001] = {};
vector<Edge> edges;

int n;
int m;

int minC = 1001;
int ans = 0;

int Find(int x){
    if(parents[x] == x)
        return x;

    return parents[x] = Find(parents[x]);
}

void Merge(int x, int y){
    x = Find(x);
    y = Find(y);

    if(x == y)
        return;

    parents[y] = x;
}

int main(){
    cin >> n >> m;

    for(int i = 1; i <= n; i++){
        parents[i] = i;
    }

    for(int i = 1; i <= n; i++){
        int val;
        cin >> val;
        minC = min(minC, val);
        vals[i] = val;
    }

    for(int i = 0; i < m; i++){
        int from, to, val;
        cin >> from >> to >> val;
        edges.push_back({ from, to, val * 2 + vals[to] + vals[from] });
    }

    sort(edges.begin(), edges.end(), [](Edge a, Edge b){
        return a.val < b.val;
    });

    for(int i = 0; i < m; i++){
        Edge e = edges[i];

        if(Find(e.from) == Find(e.to))
            continue;

        Merge(e.from, e.to);

        ans += e.val;
    };

    cout << ans + minC;
}