[백준 1991] 트리 순회

🔗 알고리즘 문제

간단한 재귀를 사용하여 구현할 수 있는 트리 문제이다. 재귀 문제를 연습하며 나름 재귀를 생각하는 능력이 올라간 느낌..?

문제 분석

이 문제는 간단하게 트리를 순회하고 순회한 결과를 출력해주면 된다.

트리를 순회하는 방식은 3가지로 나뉘는데 각각 전위 순회 중위 순회 후위 순회이다.

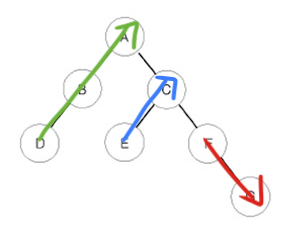
전위 순회는 다음과 같이 루트->왼쪽 자식->오른쪽 자식 순으로 순회한다.

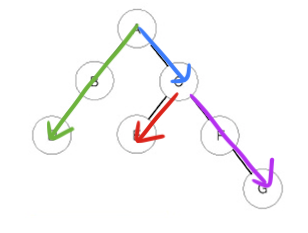
중위 순회는 다음과 같이 왼쪽 자식 -> 루트 -> 오른쪽 자식 순으로 순회한다.

마지막으로, 후위 순회는 왼쪽 자식 -> 오른쪽 자식 -> 루트 순으로 순회한다.

발상 & 알고리즘 설계

2진 트리를 구성해야 하기에 자신의 왼쪽 노드와 오른쪽 노드를 가지는 구조체를 만들어 트리를 구성해주었다.

struct Node{
    char ch;
    Node *left;
    Node *right;
};

이제 각각 전방, 중위, 후위 순회를 하는 재귀 함수를 만들고 트리를 순회해주면 된다.

void Search1(Node* node){
    if(node == nullptr)
        return;
	
    // 루트를 탐색
    ans.push_back(node->ch);
    // 왼쪽 탐색
    Search1(node->left);
    // 오른쪽 탐색
    Search1(node->right);
}

void Search2(Node* node){
    if(node == nullptr)
        return;
	
    // 왼쪽 탐색
    Search2(node->left);
    // 루트 탐색
    ans.push_back(node->ch);
    // 오른쪽 탐색
    Search2(node->right);
}

void Search3(Node* node){
    if(node == nullptr)
        return;
	
    // 왼쪽 탐색
    Search3(node->left);
    // 오른쪽 탐색
    Search3(node->right);
    // 루트 탐색
    ans.push_back(node->ch);
}

코드

#include<iostream>
#include<vector>

using namespace std;

struct Node{
    char ch;
    Node *left;
    Node *right;
};

int n;
vector<Node> v;
vector<char> ans;

void Search1(Node* node){
    if(node == nullptr)
        return;

    ans.push_back(node->ch);
    Search1(node->left);
    Search1(node->right);
}

void Search2(Node* node){
    if(node == nullptr)
        return;

    Search2(node->left);
    ans.push_back(node->ch);
    Search2(node->right);
}

void Search3(Node* node){
    if(node == nullptr)
        return;

    Search3(node->left);
    Search3(node->right);
    ans.push_back(node->ch);
}

int main(){
    cin >> n;

    for(int i = 0; i < n; i++){
        Node node = { (char)('A' + i), nullptr, nullptr };
        v.push_back(node);
    }

    for(int i = 0; i < n; i++){
        char nodeNum;
        cin >> nodeNum;
        Node* node = &v[nodeNum - 'A'];
        for(int j = 0; j < 2; j++){
            char input;
            cin >> input;
            if(input != '.'){
                if(j == 0){
                    node->left = &v[(int)(input - 'A')];
                }
                else if(j == 1){
                    node->right = &v[(int)(input - 'A')];
                }
            }
        }
    }

    Search1(&v[0]);
    for(int i = 0; i < n; i++){
        cout << ans[i];
    }
    cout << "\n";

    Search2(&v[0]);
    for(int i = n; i < n * 2; i++){
        cout << ans[i];
    }
    cout << "\n";

    Search3(&v[0]);
    for(int i = n * 2; i < n * 3; i++){
        cout << ans[i];
    }
}