링크

2xn 타일링 2

문제

2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.

아래 그림은 2×17 직사각형을 채운 한가지 예이다.

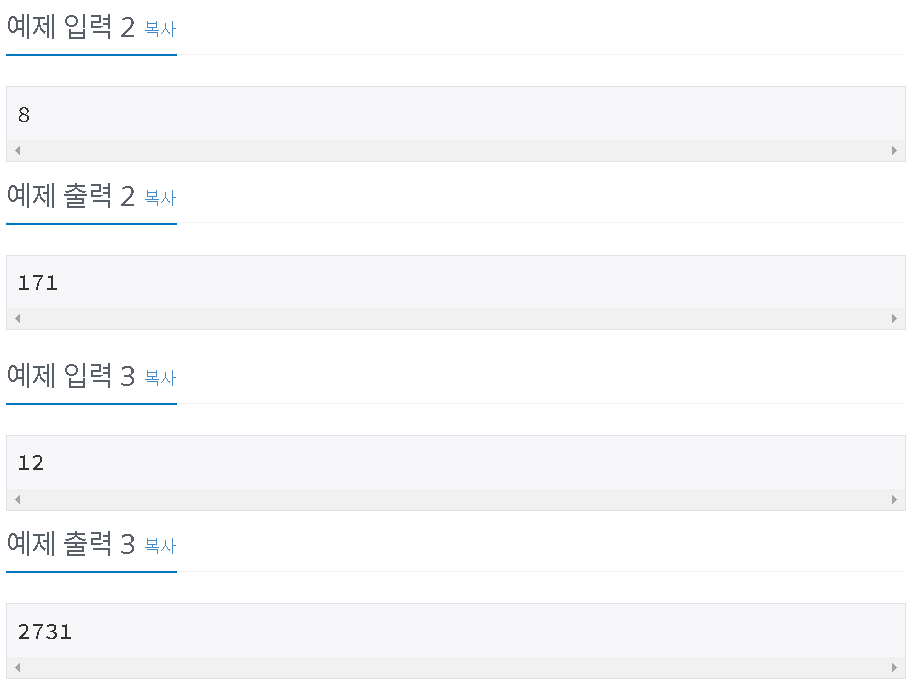
입력

첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)

출력

첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.

풀이

이러한 문제는 수를 적는것보다 각각의 모형을 그리며 접근하는 것이 더욱 효율적인 것 같다.

dp[n-1]이 있을 때 21을 채우는 도형은 1개뿐이다.
dp[n-2]일 때 22를 채우는 도형은 12도형 2개와 22도형 1개이다.
여기서 21도형 2개는 포함하지 않는다. 그러한 dp[n-1]일때 21부분을 넣어줬기 때문에 이 부분은 중복이기에 포함하지 않는다.
(솔직히 이 부분 이해 잘안간다!) 복습하쟝!

Code

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
	public static void main(String[] args) throws IOException{
		// TODO Auto-generated method stub
		BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
		int n=Integer.parseInt(br.readLine());
		
		int[] dp=new int[1001];
		dp[0]=0;
		dp[1]=1;
		dp[2]=3;
		
		for(int i=3; i<=n; i++)
		{
			dp[i]=(dp[i-1]+(2*dp[i-2]))%10007;
		}
		
		System.out.println(dp[n]);
		
    }
}