Tree
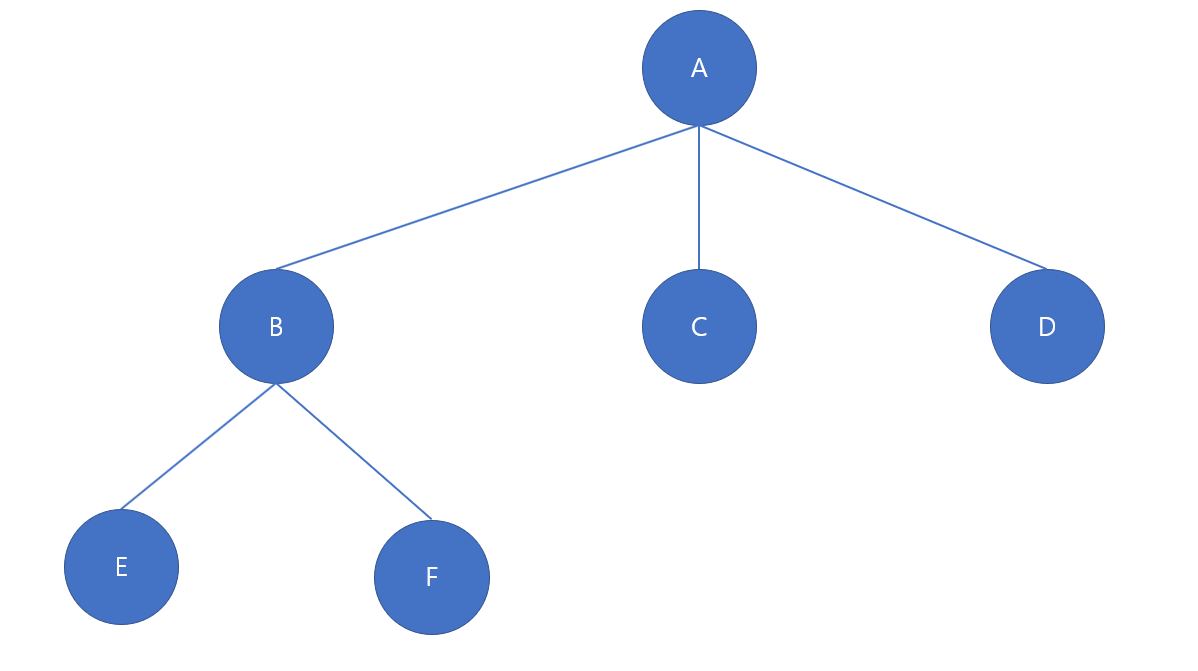
자료 구조 Tree는 나무를 거꾸로 뒤집은 형태를 가지고 있다.
데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료 구조이다.
데이터를 순차적으로 나열시킨 선형 구조가 아니라, 하나의 데이터 아래에 여러 개의 데이터가 존재할 수있는 비선형 구조. (이게 나무랑 닮아서 트리 구조가된 거임...)
이 트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가므로 사이클이 없다.
- 루트 (Root): 하나의 꼭짓점 데이터. 트리 구조의 시작점이 되는 노드를 말한다.
- 노드 (Node): 트리 구조를 이루는 모든 개별 데이터. 두개의 노드가 상하 계층으로 연결되면 부모/자식 관계를 가진다. (자식 없는 노드는 리프 노드라고 부른다.)
- 리프 (Leaf): 트리 구조의 끝 지점이고, 자식 노드가 없는 구조를 말한다.
Tree구조는 깊이, 높이, 레벨등을 측정할 수 있다.
-
깊이 (Depth)
루트에서 하위 계틍의 특정 노드까지의 깊이를 표현한다.
ex) 위 그림에서 루트 노드(A)는 깊이가 0, B, C, D는 1이다. -
레벨 (Level)
같은 깊이를 가지고 있는 노드를 묶어서 레벨로 표현한다. 같은 레벨에 나란히 있는 노드를 형제 노드라고한다.
ex) 깊이 0인 A는 레벨 1, 깊이 1인 B,C,D는 레벨2 -
높이 (Height)
리프 노드(자식없는 노드)를 기준으로 루트까지의 높이를 말한다. -
서브 트리 (Sub Tree)
Root에서 나온 큰 트리의 내부에 트리 구조를 갖춘 작은 트리를 말한다.
트리구조 사용 시 장점은 뭐가 있을까
- 효과적인 계층 구조 표현이 가능하다. (ex_조직도)
- 그래서 구조 파악이 용이하다. (시각화가 쉬우므로)
- 이진 탐색 트리,힙 같은 형태로 사용될 수 있으며, 정렬과 탐색을 위한 알고리즘을 구현하는데에 사용.
- 삽입과 삭제가 쉽다. (해당 노드의 부모와 자식노드만 수정하면 되니까)
- 데이터베이스, 알고리즘 등 다양한 분야에서 사용된다. (다양한 문제를 해결하기위한 다양한 알고리즘의 기초가되므로)
tree구조에는 대표적으로 이진 트리 (Binary Tree)구조가 있다.
이진 트리 (Binary Tree): 각 노드가 최대 2개의 자식 노드를 가지는 트리구조이다.
- 이진 탐색 트리 (Binary Search Tree = BST): 이진 트리의 일종으로, 각 노드의 왼쪽 서브 트리에는 해당 노드보다 작은 값들이, 오른쪽 서브트리에는 해당 노드보다 큰 값들이 저장되는 규칙이 있다.
- 힙 (Heap): 완전 이진 트리의 일종으로, 각 노드의 값이 자식 노드의 값보다 작거나 큰 특정 순서를 유지하는 구조이다.
최소 힙 (Min Heap)에서는 부모 노드의 값이 자식 노드의 값보다 작거나 같으며, 최대 힙(Max Heap)에서는 부모 노드의 값이 자식 노드의 값보다 크거나 같다. - 트라이 (Trie): 문자열을 저장하고 검색하는 데 특화된 트리구조로, 각 노드가 여러 자식 노드를 가질 수 있으며, 각 노드는 문자열의 한 문자를 저장한다.
트라이는 문자열 검색, 자동 완성, IP 라우팅의 목적으로 사용된다. - 레드-블랙 트리: 이진 탐색 트리의 또 다른 확장으로, 노드에 색깔이 부여되어 특정 규칙을 만족하며 균형을 유지한다. 이 규칙 덕분에 탐색, 삽입, 삭제 연산의 시간 복잡도가 O(log N)을 유지한다.
(이진 트리와 관련해선 다음 페이지에서 설명하겠다.. )
Graph
그래프는 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료 구조이다.
그래프라는 이름이라 어떤 데이터를 그래프로 표현하는 건가,,? 했는데 전혀 아니었다.
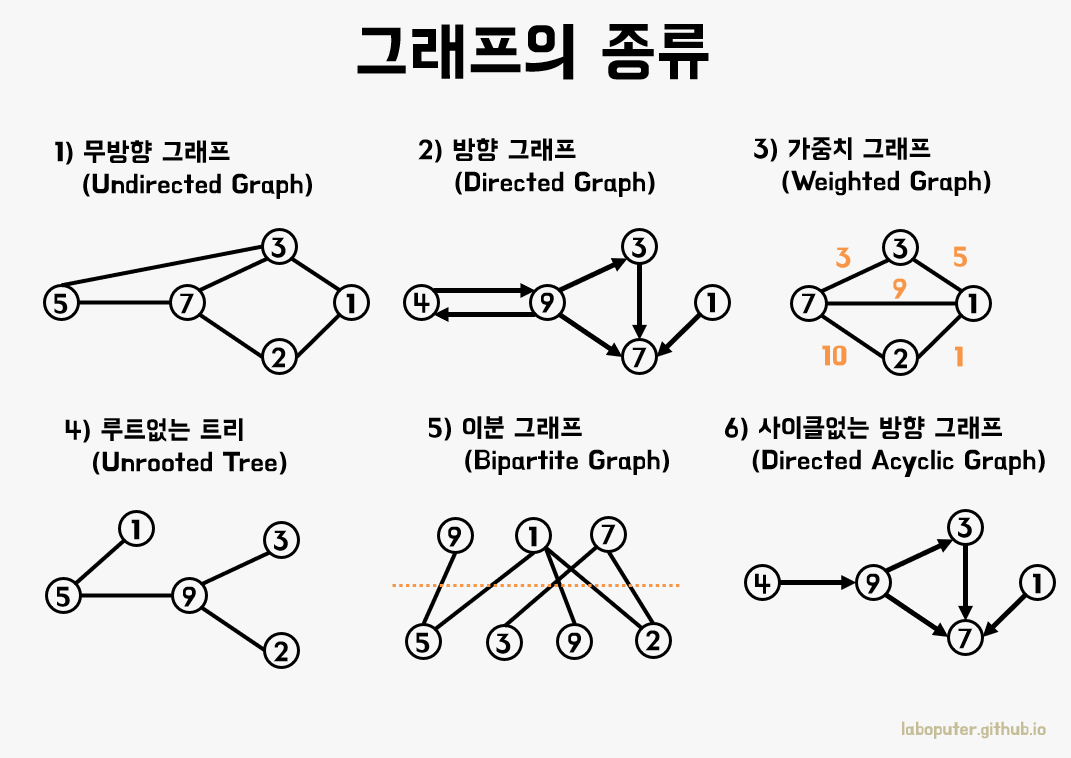
위 그림처럼 여러 점들이 선으로 이어져있고, 여러개가 걸쳐져 있는 구조이다.
Graph의 구조
- 직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 있다.
- 간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어진다.
Graph의 표현방식
- 인접 행렬
두 정점을 바로 이어주는 간선이 있다면, 이 두 정점은 인접한다고 말한다.
인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로 2차원 배열의 형태로 나타낸다.
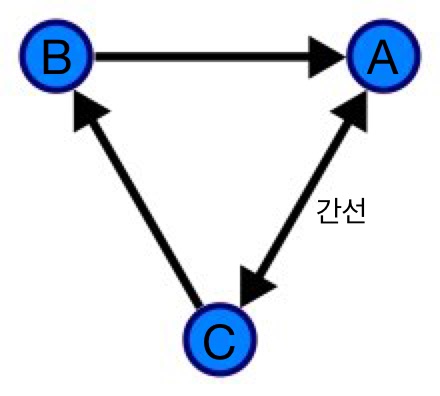
위 이미지와 같은 그래프를 인접 행렬로 표시하면
int[][] matrix = new int[][]{
{0, 0, 1}, // A정점에서 이동 가능한 정점을 나타내는 행
{1, 0, 1}, // B정점에서 이동 가능한 정점을 나타내는 행
{1, 0, 0}. // C정점에서 이동 가능한 정점을 나타내는 행
}; -
A의 진출차수는 1개입니다: A —> C
[0][2] == 1 -
B의 진출차수는 2개입니다: B —> A, B —> C
[1][0] == 1
[1][2] == 1 -
C의 진출차수는 1개입니다: C —> A
[2][0] == 1
- 인접 리스트
인접 리스트는 각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 표현한다.
각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고있다.
위 그래프를 인접 리스트로 표현하면 아래 이미지와 같다.

이걸 인접 리스트로 표시하면,
// A, B, C는 각각의 인덱스로 표기합니다. 0 == A, 1 == B, 2 == C
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
graph.add(new ArrayList<>(Arrays.asList(2, null)));
graph.add(new ArrayList<>(Arrays.asList(0, 2, null)));
graph.add(new ArrayList<>(Arrays.asList(0, null)));
graph.get(0) == [2, null] == 0 -> 2 -> null
graph.get(1) == [0, 2, null] == 1 -> 0 -> 2 -> null
graph.get(2) == [0, null] == 2 -> 0 -> null간선이 오는 순서는 보통 중요하지 않다. 그래프, 트리, 스택, 큐 등 모든 자료구조는 구현하는 사람의 편의와 목적에 따라 기능을 추가/삭제할 수 있다.
그래프를 인접 리스트로 구현할 떄, 정점별로 봐야할 우선순위를 고려해 구현할 수 있다. 이떄, 리스트에 담긴 정점들을 우선순위별로 정렬할 수 있으며, 우선 순위가 없으면 연결된 정점들을 단순하게 나열한 리스트가 된다.
우선 순위를 다뤄야한다면 더 적합한 자료구조 (ex_ Queue, Heap)를 사용하는 것이 합리적이라 그래프를 인접 리스트로 구현할 때 순서는 보통! 중요하지 않다. (하지만 언제나 예외는 있다는 사실)
그럼 인접 리스트는 언제 사용하느냐?
- 메모리를 효율적으로 사용하고 싶을 때 사용한다.
인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지한다.
그래프 자료구조에서는 다음과 같은 용어들을 사용한다.
- 정점(vertex): 노드라고도 하며 데이터가 저장되는 그래프의 기본 원소이다. (하나의 점을 말한다.)
- 간선(edge): 정점 간의 관계를 나타낸다. (하나의 선을 말한다.)
- 인접 정점 (adjacent vertex): 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점을 말한다.
- 가중치 그래프 (weighted Graph): 연결의 강도가 적혀있지 않는 그래프를 말한다.
- 비가중치 그래프 (unweighted Graph): 연결의 강도가 적혀있지 않는 그래프를 말한다.
- 무향 (무방향) 그래프(undirected Graph):
- 진입 차수 (in-degree)/ 진출 차수(out-degree):한 정점에 진입하고 진출하는 간선이 몇 개인지 나타낸다.
- 인접 (adjacency): 두 정점 간에 간선이 직접 이어져있다면 이 두 정점은 인접한 정점이다.
- 자기 루프 (self loop):다른 정점을 거치지 않는다. 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다고 표현한다.
- 사이클 (cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다.
