[자료구조] 이진 탐색 트리 (Binary Search Tree)

☑️ 이전 게시물에서 Tree구조에 대해 내용을 정리했었다.
☑️ 이 게시물에서는 이진 탐색과 이진 탐색 트리(BST)에 대해 좀 더 자세히 정리하려한다.

이전 게시물 - Tree구조

---

이진 탐색

자식 노드가 최대 두개인 노드들로 구성된 Tree구조이다.
자료의 삽입, 삭제 방법에 따라

• 정 이진 트리 (Full binary tree) : 각 노드가 0개 혹은 2개의 자식 노드를 가진다.

• 포화 이진 트리 (Perfect binary tree) : 정 이진 트리이면서, 완전 이진 트리인 경우이다.
  모든 리프 노드의 레벨이 같고, 모든 레벨이 가득 채워져있는 tree이다.

• 완전 이진 트리 (Complete binary tree) : 마지막 레벨을 제외한 모든 노드가 가득 차 있고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져있어야한다.

---

이진 탐색 트리 (Binary Search Tree)

이진 탐색의 속성이 이진 트리에 적용된 특별한 형태의 이진 트리이다.
그니까 이진 탐색이 뭐냐?
이진 탐색 알고리즘이란, 정렬된 데이터 중에서 특정한 값을 찾기 위한 탐색 알고리즘 중 하나이다.
오름차순으로 정렬된 데이터를 같은 크기의 두 부분으로 나눈 후, 두 부분 중 탐색이 필요한 부분에서만 탐색하도록 탐색 범위를 제한하여 원하는 값을 찾는 알고리즘이다.

1. 전체 데이터에서 중간(Root)에서 내가 찾고자 하는 값이 있는지 확인한다.
2. 중간값이 내가 찾고자 하는 값이 아닐 경우, 오름차순으로 정렬된 데이터에서 중간값보다 큰 값인지 작은 값인지 판단한다.
3. 찾고자 하는 값이 중간값보다 작은 값일 경우, 데이터의 맨 앞부터 중간값 전까지의 범위를 탐색 범위로 잡고 탐색을 반복 수행한다.
4. 찾고자 하는 값이 중간값보다 큰 값일 경우, 데이터의 중간값의 다음 값부터 맨 마지막까지를 탐색 범위로 잡고 탐색을 반복 수행한다.

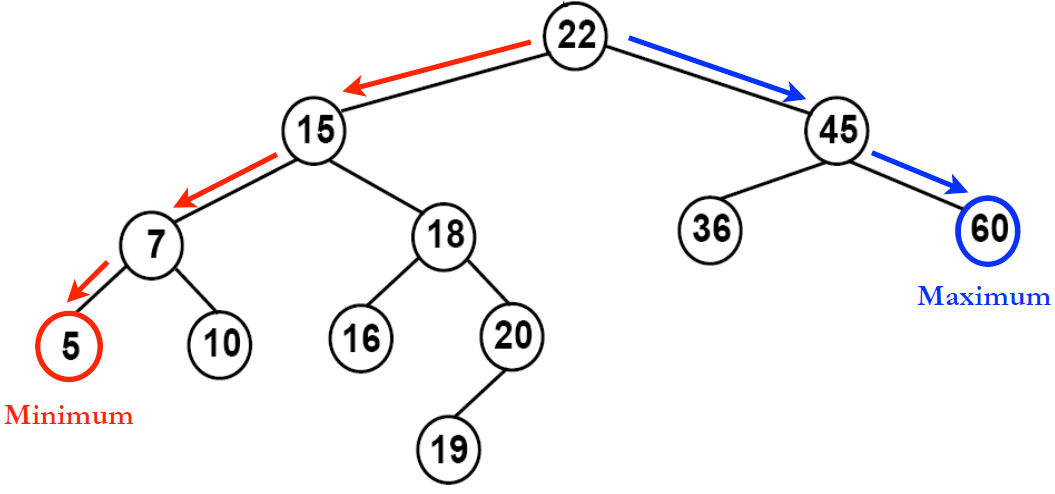
이진 탐색 트리(BST)를 정리하면,

모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있다.

BST는 기존 이진 트리보다 탐색이 빠르다. BST의 연산은 트리의 높이가 h라면 O(h) 의 복잡도를 가진다.

BST의 탐색 과정

1. 루트 노드의 키와 찾고자 하는 값을 비교한다. 만약 찾고자하는 값이면 탐색 종료.
2. 찾고자 하는 값이 루트 노드의 키보다 작다면, 왼쪽 서브 트리로 탐색 진행
3. 찾고자 하는 값이 루트 노드의 키보다 크면, 오른쪽 서브 트리로 탐색 진행

이과정을 값을 찾을 때까지 반복해 진행한다. 그래서 트리 안의 값을 찾는다면 무조건 트리의 높이(h) 이하의 탐색이 이루어지는 것이다.
여기서 주의할 점은, 트리안에 내가 찾고자하는 값이 없더라도 최대 h번 만큼 연산 및 탐색이 진행된다는 것이다.

BST에서 노드의 추가/삭제 방법
1) 노드를 추가하려할 때:
노드의 값이 현재 노드보다 작으면 왼쪽 서브 트리에, 크면 오른쪽 서브 트리에 추가한다. 이 작업은 노드를 삽입하려는 위치까지 재귀적으로 탐색하며 이루어진다.

2) 노드를 삭제하려할 때:
삭제할 때는 아래 경우를 고려해야한다.

• 삭제할 노드가 리프 노드인 경우 : 자식 노드가 없기 때문에 그냥 삭제하면 된다.

• 삭제할 노드의 자식 노드가 하나인 경우 : 삭제할 노드의 부모노드와 자식 노드를 연결해준다.

• 삭제할 노드의 자식 노드가 두개인 경우 : 삭제할 노드를 대체할 노드를 찾아서 서로 교환한 뒤 삭제해준다. 이 작업을 재귀적으로 수행하면서 트리의 구조를 유지한다.