알고리즘의 복잡도는 문제를 해결할 때 있어서 얼마만큼의 자원을 소모하는지를 나타내고, 알고리즘의 성능과 효율성을 측정하는 데 중요한 개념이다. 알고리즘의 복잡도는 시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)로 나뉜다. 이번 글에서는 시간 복잡도를 위주로 다룰 것이기 때문에 공간 복잡도는 알고리즘을 실행하는데 사용하는 물리적 저장 공간의 크기 정도로 이야기하고 넘어가겠다.
시간 복잡도(Time Complexity)
시간 복잡도(Time Complexity)는 알고리즘의 성능을 평가하는 중요한 요소이다. 시간 복잡도는 알고리즘의 절대적인 수행 시간을 나타내는 것이 아니라 알고리즘을 이루고 있는 연산들이 몇 번이나 수행되는지를 숫자로 표시한다.
알고리즘의 시간 복잡도는 3가지 경우로 나누어 평가할 수 있다.
- 최악 시간 복잡도(Worst-case Time Complexity)
가장 긴 시간을 소요하게 만드는 입력에 따라 소요되는 시간 - 평균 시간 복잡도(Average Time Complexity)
임의의 입력 패턴을 가정했을 때 소요되는 시간의 평균 - 최선 시간 복잡도(Best-case Time Complexity)
최악의 경우의 반대 의미로, 가장 짧은 시간을 소요하게 만드는 입력에 따라 소요되는 시간
최악의 경우의 수행시간이 알고리즘의 시간 복잡도 척도로 많이 쓰인다. 여기서 최악의 경우란 입력 자료 집합을 알고리즘에 최대한 불리하도록 만들어서 얼마만큼의 시간이 소모되는 지를 분석하는 것이다.
시간 복잡도의 표기법
점근 표기법(asymptotic notation)은 알고리즘의 복잡도 함수의 증가 양상을 구분하기 위해 사용하는 표기법이다.
- 상한 점근: 아무리 느려봤자 f(n) 정도이다. f(n)보다 빠르거나 같다. ⇒ Big-O(빅-오)
- 하한 점근: 아무리 빨라봤자 f(n) 정도이다. f(n)보다 느리거나 같다. ⇒ Big-Ω(빅-오메가)
- 차수: 상한과 하한의 교집합 ⇒ Big-θ(빅-세타)
위 세 가지 표기법은 시간 복잡도의 각각 최악, 최선, 평균의 경우에 대하여 나타내는 방법이다. 대부분 시간 복잡도를 말 할 때, 최악의 경우로 말하기 때문에 Big-O 표기법을 사용하는게 일반적이다. 따라서 Big-O 표기법에 대해 조금 더 알아보자.
Big-O 표기법
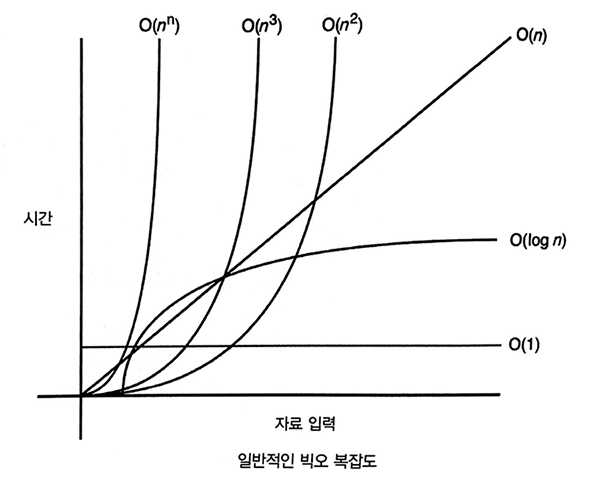
다음은 많이 쓰이는 Big-O 표기법을 순서대로 표시한 것이다.
- O(1): 상수형
- O(log n): 로그형
- O(n): 선형
- O(n log n): 선형로그형
- O(n²): 2차형
- O(n³): 3차형
- O(2ⁿ): 지수형
- O(n!): 팩토리얼형
Big-O 표기법은 입력의 개수에 따라 기본 연산 수행 횟수를 개략적으로 나타낸 것이기 때문에 대략적인 수행시간을 추정해 볼 수 있다. 다음은 Big-O 표기법에 의한 알고리즘의 수행시간을 비교한 것이다.
O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ) < O(n!)
입력값이 커짐에 따라 계수의 의미는 점차 줄어든다. 따라서 Big-O 표기법에서는 계수를 생략하고 표현한 것을 볼 수 있다.
시간 복잡도 구하기
다음은 코딩 테스트 알고리즘 문제를 풀면서 본인이 푼 문제의 시간 복잡도를 간단하게 구해보기 위한 방법이다.
- 하나의 반복문에서 단일 요소 집합을 반복 하는 경우 : O(n)
- 컬렉션의 절반 이상을 반복 하는 경우 : O(n/2) -> O(n)
컬렉션 자료형(Collection data type)은 여러 개의 값을 모아서 하나의 변수에 저장할 수 있는 자료형이다. 파이썬에서는 리스트(List), 튜플(Tuple), 셋(Set), 딕셔너리(Dictionary) 등이 대표적인 컬렉션 자료형이다.
- 이중 반복문을 사용하여 각각의 컬렉션을 반복할 경우 : O(n + m) -> O(n)
- 이중 반복문을 사용하여 단일 컬렉션을 반복하는 경우 : O(n²)
- 이중 반복문을 사용하여 서로 다른 두 개의 컬렉션을 반복 할 경우 : O (n² + m²) -> O (n²)
- 컬렉션 정렬을 사용하는 경우 : O(n*log(n))
