[자료구조] 연결 리스트(Linked List)

연결 리스트(Linked List)란?

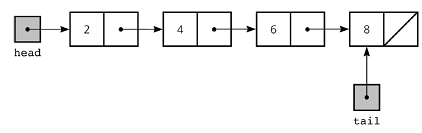
연결 리스트(Linked List)는 데이터를 노드(Node)라고 불리는 객체들로 나누고, 각 노드가 다음 노드를 가리키는 포인터를 가지고 있는 자료 구조이다. 각 노드는 데이터와 포인터를 가지며, 이 포인터를 통해 다음 노드를 가리킨다. 연결 리스트의 가장 첫 번째 노드는 Head 노드라고 부르고 마지막 노드는 Tail 노드라고 부른다.

배열(Array vs Linked Lists)

연결 리스트는 배열(Array)과는 달리 데이터를 순차적으로 저장하지 않기 때문에, 데이터의 삽입과 삭제가 빠르고 유연하게 이루어질 수 있다. 이는 연결 리스트가 동적(Dynamic)으로 크기가 조절될 수 있기 때문이다. 하지만 배열과는 다르게 인덱싱(Indexing)을 통한 데이터 접근이 불가능하기 때문에, 특정 위치에 있는 데이터에 접근하려면 전체 노드를 순회해야 한다. 두 자료구조의 차이를 명확히 구분하기 위해 각각의 특징을 정리해보았다.

Array(배열)

• 논리적 저장순서와 물리적 저장 순서가 일치
• 인덱스로 시간 복잡도 O(1)만에 해당 원소에 접근
  (즉, Random Access 가능)
• 제한적인 크기를 가짐
• 삭제 또는 삽입 연산시에 해당 원소에 접근하여 작업을 완료한 뒤 Shift를 해주기 때문에 O(n)의 시간복잡도를 갖는다.
  (삭제 : 삭제 원소보다 인덱스가 큰 원소들 Shift, 삽입 : 다른 모든 원소 인덱스 1씩 Shfit)
• 검색이 잦은 경우에 유리

Linked List(연결 리스트)

• 논리적 저장순서와 물리적 저장 순서가 불일치
  (자료의 주소 값으로 노드를 이용해 서로 연결되어 있는 구조)
• 데이터를 추가 할때마다 동적으로 크기가 늘어남
• 원소 검색 시 첫번째 Node부터 마지막 Node까지 일일이 확인하기 때문에 O(n)의 시간 복잡도를 가짐
• 삽입 또는 삭제 연산시에 해당 원소를 검색한 후 삭제, 삽입 연산이 이루어지므로 O(n)의 시간 복잡도를 가짐
  (맨 앞이나 맨 뒤에 원소를 삭제 하거나 삽입 한다면 시간 복잡도는 O(1))
• 삽입, 삭제가 잦은 경우에 유리

연결 리스트의 연산과 구현

연결 리스트의 연산은 크게 다음과 같다

• 연결 리스트의 길이 얻어내기
• 리스트 순회
• 특정 원소 참조
• 원소 삽입
• 원소 삭제
• 두 리스트 합치기

연결 리스트의 각 연산을 구현한 파이썬 코드는 다음과 같다. 해당 코드는 싱글 링크드 리스트(Single Linked List)에 대한 경우이다.

class Node:

	def __init__(self, item):
		self.data = item
		self.next = None


class LinkedList:

	def __init__(self):
		self.nodeCount = 0
		self.head = Node(None)
		self.tail = None
		self.head.next = self.tail

	# 리스트 출력
	def __repr__(self):
		if self.nodeCount == 0:
			return 'LinkedList: empty'

		s = ''
		curr = self.head
		while curr.next:
			curr = curr.next
			s += repr(curr.data)
			if curr.next is not None:
				s += ' -> '
		return s

    # 리스트 길이 얻어 내기
	def getLength(self):
		return self.nodeCount
        
	# 리스트 순회
	def traverse(self):
		result = []
		curr = self.head
		while curr.next:
			curr = curr.next
			result.append(curr.data)
		return result

	# 특정 위치 원소 참조
	def getAt(self, pos):
		if pos < 0 or pos > self.nodeCount:
			return None

		i = 0
		curr = self.head
		while i < pos:
			curr = curr.next
			i += 1

		return curr


	def insertAfter(self, prev, newNode):
		newNode.next = prev.next
		if prev.next is None:
			self.tail = newNode
		prev.next = newNode
		self.nodeCount += 1
		return True

	# 원소 삽입
	def insertAt(self, pos, newNode):
		if pos < 1 or pos > self.nodeCount + 1:
			return False

		if pos != 1 and pos == self.nodeCount + 1:
			prev = self.tail
		else:
			prev = self.getAt(pos - 1)
		return self.insertAfter(prev, newNode)
       
    # 원소 삭제
    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError

        if pos == 1:
            curr = self.head 
            self.head = curr.next 
            if self.nodeCount == 1:
                self.tail = self.head

        else:
            prev = self.getAt(pos-1)
            curr = prev.next 
            prev.next = curr.next
            if pos == self.nodeCount:
                self.tail = prev 

        self.nodeCount -= 1
        return curr.data

	# 두 리스트 합치기
	def concat(self, L):
		self.tail.next = L.head.next
		if L.tail:
			self.tail = L.tail
		self.nodeCount += L.nodeCount

지금까지 살펴본 내용은 단일 연결 리스트에 대한 내용이다. 하지만 이중 연결 리스트가 더욱 유용하고 많이 사용된다.

이중 연결 리스트(Doubly Linked List)

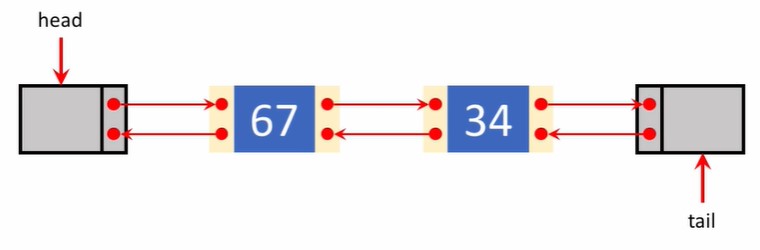
이중 연결 리스트(Doubly Linked List)는 링크드 리스트의 일종으로, 각 노드가 데이터와 이전 노드와 다음 노드를 가리키는 두 개의 포인터를 가지고 있는 자료 구조이다.

각 노드는 데이터를 저장하고, prev 포인터는 이전 노드를 가리키고, next 포인터는 다음 노드를 가리킨다. 이전 노드를 가리키는 포인터가 추가되었기 때문에, Doubly Linked List는 양방향으로 순회할 수 있다.

Doubly Linked List의 특징은 다음과 같다.

• 삽입과 삭제가 빠르다.
• 양방향으로 순회가 가능하다.
• 어떤 노드의 이전 노드와 다음 노드를 쉽게 찾을 수 있다.
• 각 노드가 두 개의 포인터를 가지기 때문에 메모리 공간을 더 사용한다.

이중 연결 리스트의 연산과 구현

이중 연결 리스트는 단일 연결 리스트보다 더 많은 연산을 수행할 수 있다. 예를 들어 역순회나, 이전 노드 삭제 같은 연산도 가능하다.

다음은 파이썬으로 구현한 이중 연결 리스트의 코드이다.

class Node:

    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None


class DoublyLinkedList:

    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None

	# 리스트 출력
    def __repr__(self):
        if self.nodeCount == 0:
            return 'LinkedList: empty'

        s = ''
        curr = self.head
        while curr.next.next:
            curr = curr.next
            s += repr(curr.data)
            if curr.next.next is not None:
                s += ' -> '
        return s

	# 리스트 길이 얻어 내기
    def getLength(self):
        return self.nodeCount

	# 리스트 순회
    def traverse(self):
        result = []
        curr = self.head
        while curr.next.next:
            curr = curr.next
            result.append(curr.data)
        return result
        
    # 리스트 역방향 순회    
    def reverse(self):
        result = []
        curr = self.tail
        while curr.prev.prev:
            curr = curr.prev
            result.append(curr.data)
        return result

	# 특정 위치 원소 참조
    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None

        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1

        return curr

	# 다음 위치에 원소 삽입
    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True
        
    # 이전 위치에 원소 삽입
    def insertBefore(self, next, newNode):
        prev = next.prev
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True

	# 지정 위치에 원소 삽입
    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode)
        
    # 다음 위치에 원소 삭제    
    def popAfter(self, prev):
        item = prev.next.data
        next = prev.next.next
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return item

	# 이전 위치에 원소 삭제   
    def popBefore(self, next):
        item = next.prev.data
        prev = next.prev.prev
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return item

	# 지정 위치에 원소 삭제 
    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError

        if pos is 1:
            return self.popAfter(self.head)
        else:
            prev = self.getAt(pos-1)
            return self.popAfter(prev)
            
    # 두 리스트 병합         
    def concat(self, L):
        self.tail.prev.next = L.head.next
        L.head.next.prev = self.tail.prev
        self.tail = L.tail

        self.nodeCount = self.nodeCount + L.nodeCount