Tree traversal

어떤 특정 목적을 위헤 트리의 모든 노드를 한번씩 방문하는 것을 트리 순회라고 한다.
계층적 구조라는 특별한 특징 때문에 모든 노드를 순회하는 방법은 여러가지가 있다.
트리를 순회할 수 있는 방법은 크게 전위 순회, 중위 순회, 후위 순회 세 가지로 나뉜다.
전, 중, 후의 기준은 루트로, 루트를 어디에 두느냐에 따라서 순회 방식이 달라진다.
이 순회 방식과는 논외로, 순회할 때의 순서는 항상 왼쪽에서 오른쪽으로 가게 된다.

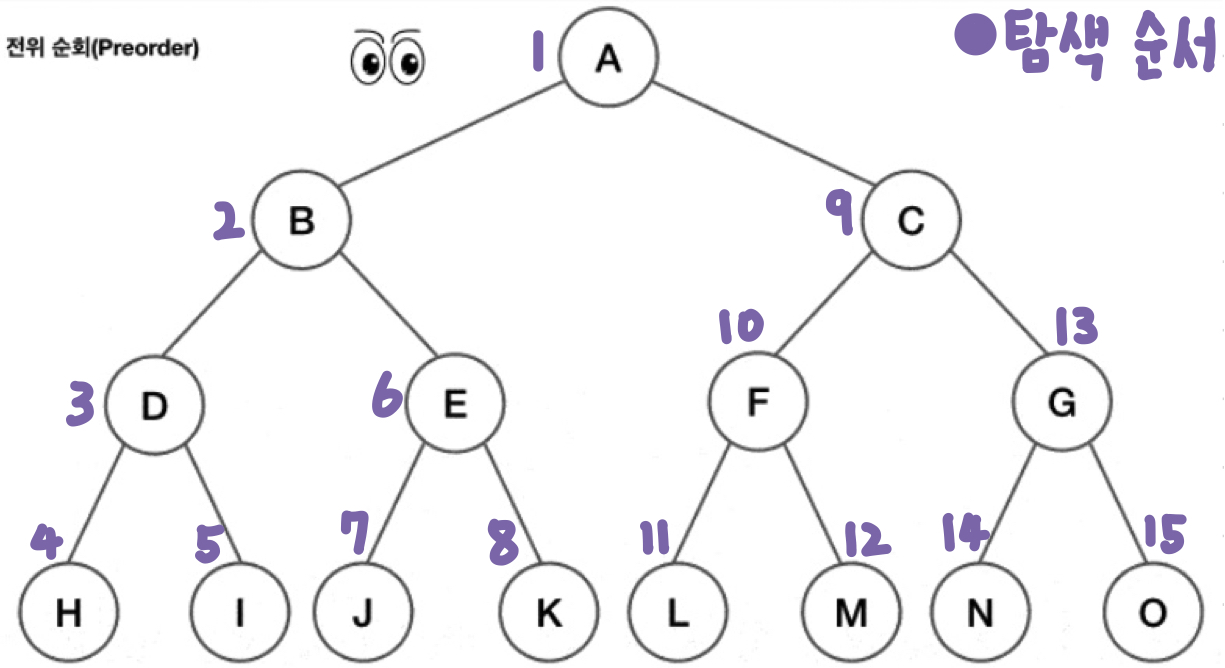
전위 순회(Preorder)

제일 처음 방문할 노드는 루트이다. 루트를 기준으로 왼쪽의 노드들을 둘러본 뒤, 왼쪽의 노드 탐색이 끝나면 오른쪽 탐색을 한다.

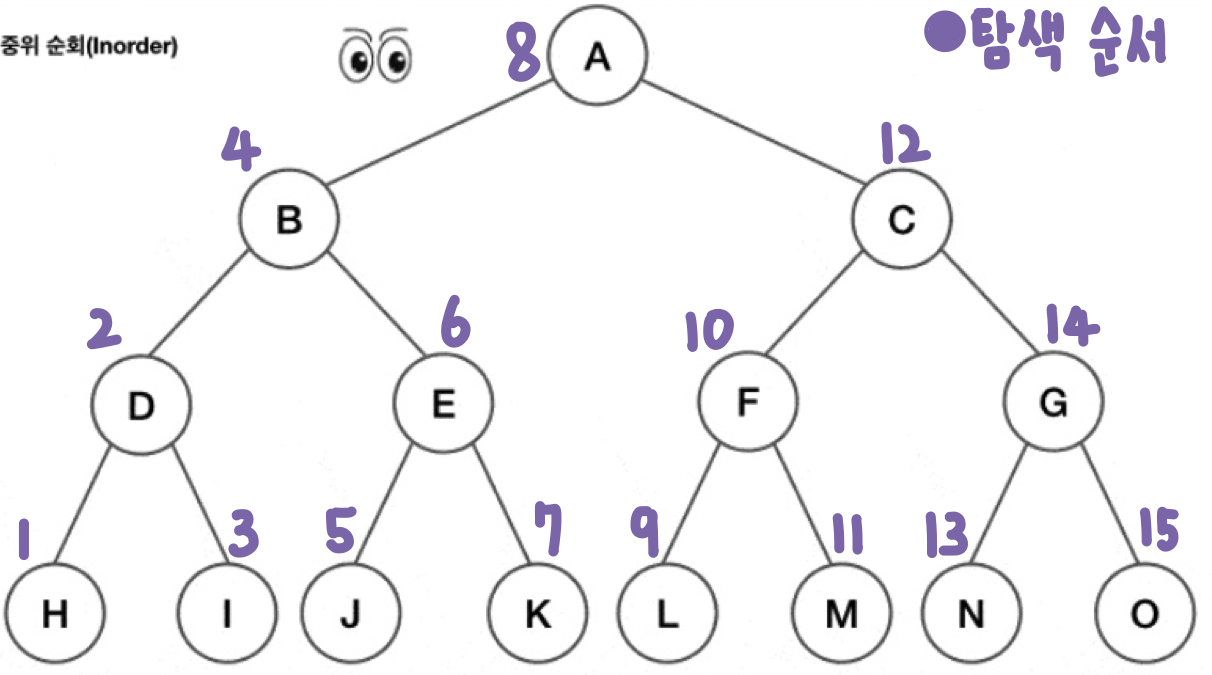
중위 순회(Inorder)

루트를 가운데 두고 순회한다. 제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 기준으로 왼쪽에 있는 노드의 순회가 끝나면 루트를 거쳐 오른쪽에 있는 노드로 이동하여 마저 탐색한다.

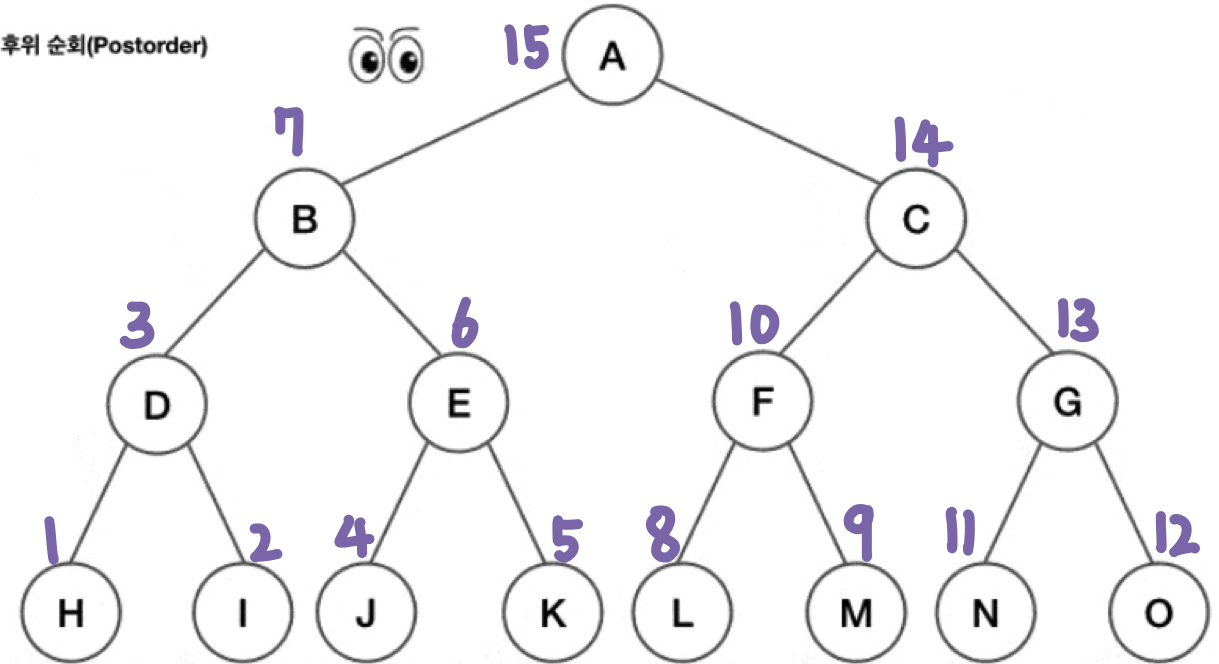
후위 순회(Postorder)

루트를 제일 마지막으로 순회한다. 제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 거치지 않고 오른쪽으로 이동해 순회한 뒤, 제일 마지막으로 루트를 방문한다.

Binary Search Tree 구현

class BinarySearchTree {
  constructor(value) {
    // constructor로 만든 객체는 이진 탐색 트리의 Node가 된다.
    this.value = value;
    this.left = null;
    this.right = null;
  }
  insert(value) { // 이진 탐색 트리의 삽입하는 메서드
    // 입력값을 기준으로, 현재 노드의 값보다 크거나 작은 것에 대한 조건문이 필요
    // 보다 작다면, Node의 왼쪽이 비어 있는지 확인 후 값을 넣는다.
    if(value < this.value) {
      if(this.left === null) {
        this.left = new BinarySearchTree(value);
      } else {
        // 비어 있지 않다면 해당 노드로 이동하여 처음부터 다시 크거나 작은 것에 대한 조건문을 확인
        this.left.insert(value);
      }
      // 보다 크다면, Node의 오른쪽이 비어 있는지 확인 후 값을 넣는다.
    } else if(value > this.value) {
      if(this.right === null) {
        this.right = new BinarySearchTree(value);
      } else {
        this.right.insert(value);
      }
    } else {
      // 아무것도 하지 않는다
    }
  }
  constains(value) {
    // 값이 포함되어 있다면 true 반환
    if(value === this.value) {
      return true;
    }
    if(value < this.value) {
      // 현재 노드의 왼쪽이 비어 있지 않고, 노드의 값이 입력값과 일치하면 true
      // 일치하지 않다면 왼쪽 노드로 이동하여 다시 탐색
      if(this.value === null) {
        return false;
      } else {
        return this.left.contains(value)
      }
    }
    if(value > this.value) {
      // 현재 노드의 오른쪽이 비어 있지 않고, 노드의 값이 입력괎과 일치하면 true
      // 일치하지 않다면 오른쪽 노드로 이동하여 다시 탐색
      if(this.right === null) {
        return false;
      } else {
        return this.right.contains(value)
      }
    }
    // 없다면 false 반환
    else {
      return false;
    }
  }
  // 트리의 순회 구현
  // 이진 탐색 트리를 전위 순회하는 메서드
  preorder(callback) {
    callback(this.value);
    if(this.left) {
      this.left.preorder(callback);
    };
    if(this.right) {
      this.right.preorder(callback);
    };
  }
  // 이진 탐색 트리를 중위 순회하는 메서드
  inoder(callback) {
    if(this.left) {
      this.left.inoder(callback);
    };
    callback(this.value);
    if(this.right) {
      this.right.inoder(callback);
    };
  }
  // 이진 탐색 트리를 후위 순회하는 메서드
  postoder(callback) {
    if(this.left) {
      this.left.postoder(callback);
    }
    if(this.right) {
      this.right.posroder(callback);
    }
    callback(this.value);
  }
}

BFS / DFS

그래프의 탐색은 하나의 정점을 시작으로 그래프의 모든 정점들을 한 번씩(탐색)하는 것을 목적으로 삼는다.
그래프의 데이터는 배열처럼 정렬이 되어 있지 않아 원하는 자료를 찾을 때까지 하나씩 모두 방문하여 찾기 때문이다.
그래프의 모든 정점 탐색 방법은 한 가지가 아니라 여러가지가 있는 데 그 중 가장 대표적으로 두 가지 방법을 꼽을 수 있다.(바로 DFS와 BFS)
이 둘은 모두 어떤 순서로 탐색을 하느냐만 다를 뿐, 모든 자료를 하나씩 확인해 본다는 점은 같다.

예시

한국에서 미국으로 가는 비행기를 예약하려고 할 때 다양한 여정 중, 최단 경로를 알아내려면 어떻게 해야 할까?

Breathed First Search

한국을 기준으로 미국까지 가는 방법을 가까운 정점부터 확인한다.
더는 탐색할 정점이 없을 때, 그 다음 떨어져 있는 정점을 순회한다.
이렇게 너비를 우선적으로 탐색하는 방법을 Breadth - First Search, 너비 우선 탐색이라고 한다.
주로 두 정점 사이의 최단 경로를 찾고 싶을 때 사용한다.
만약, 경로를 하나씩 전부 방문하는 방식으로 하게 된다면, 최악의 경우에는 모든 경로를 다 살펴보게 될지도 모른다.

Depth First Search

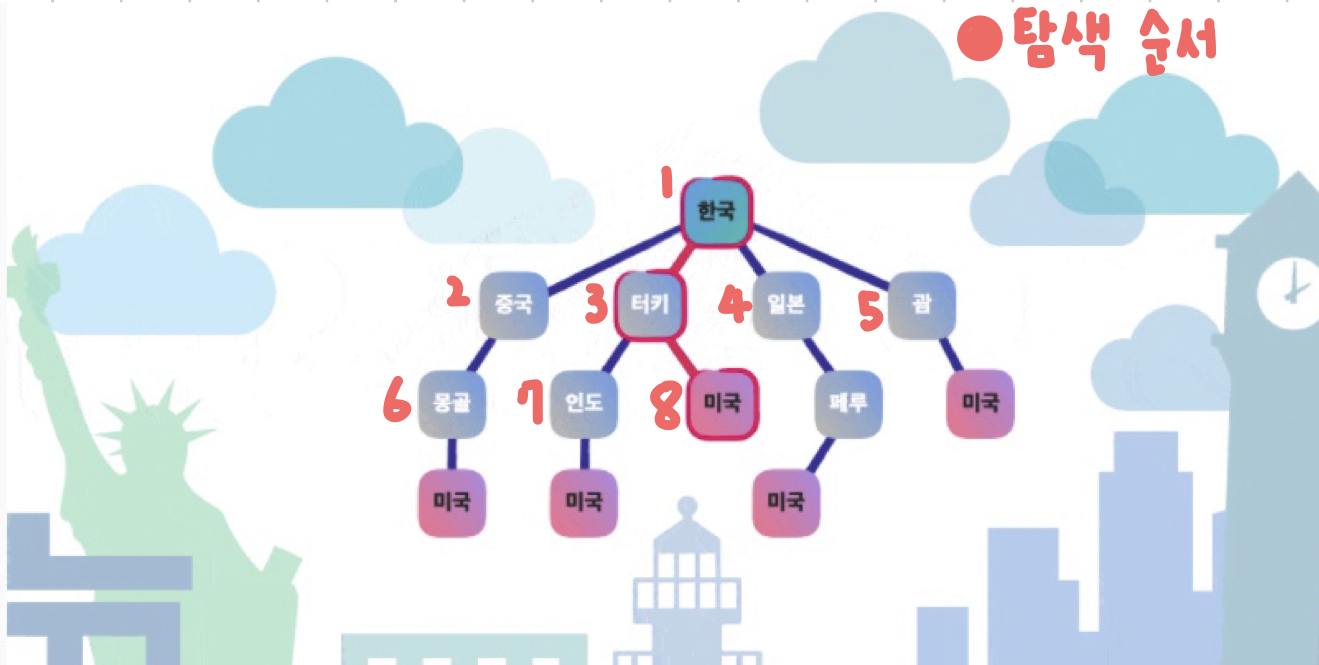
어떤 경로가 미국으로 가는 것인지 모르기 때문에, 하나의 경로를 끝까지 탐색한 후, 미국 도착이 아니라며면 다음 경로로 넘어가 탐색한다.
이렇게 깊이를 우선적으로 탐색하는 방법을 Depth - First Search, 깊이 우선 탐색이라고 한다.
한 정점에서 시작해서 다음 경로로 넘어가기 전에 해당 경로를 완벽하게 탐색하고 싶을 때 사용한다.
BFS보다 탐색 시간은 늦을지라도 모든 노드를 완전히 탐색할 수 있다.
만약 BFS로 탐색을 하게 된다면 제일 첫 번째 경로가 미국행일지라도, 모든 경로를 하났기 살펴보아야 하는 불상사가 발생하게 된다.

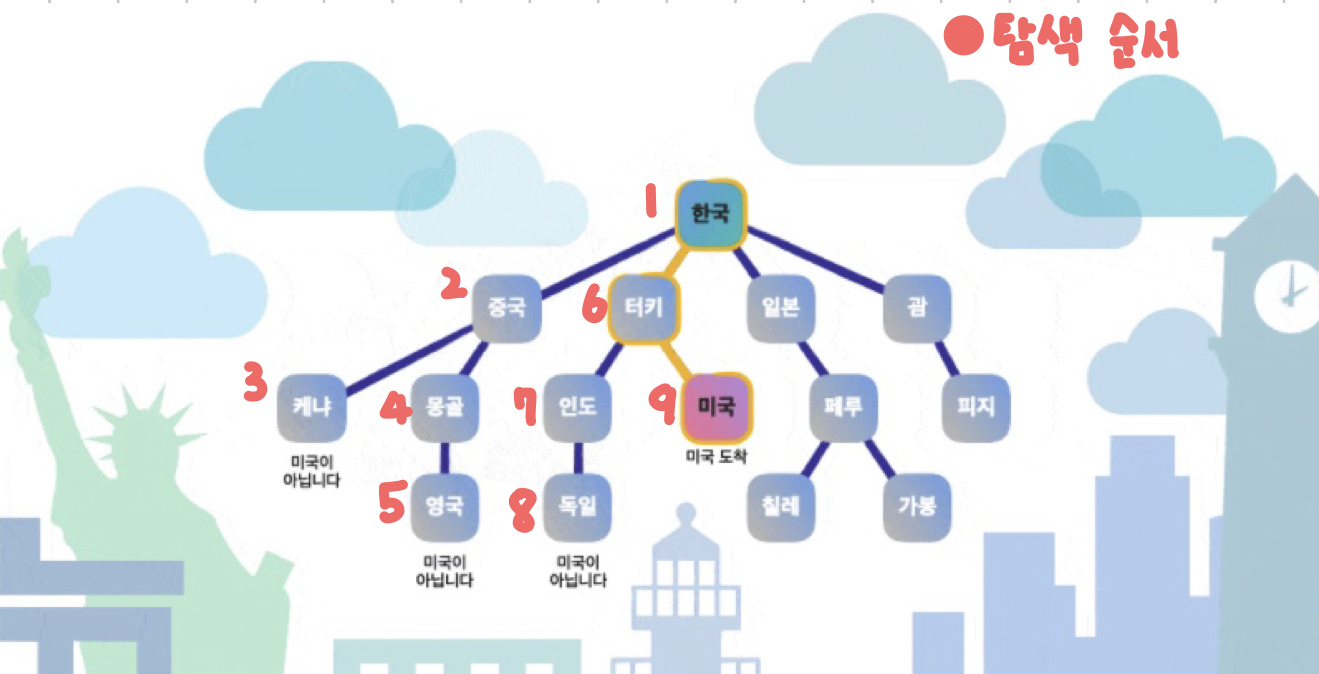
BFS와 DFS는 모든 정점을 한번만 방문한다는 공통점을 가지고 있지만, 사용할 때의 장단점은 분명하기 때문에 해당 상황에 맞는 기법을 사용해야한다.