LeetCode - Critical Connections in a Network

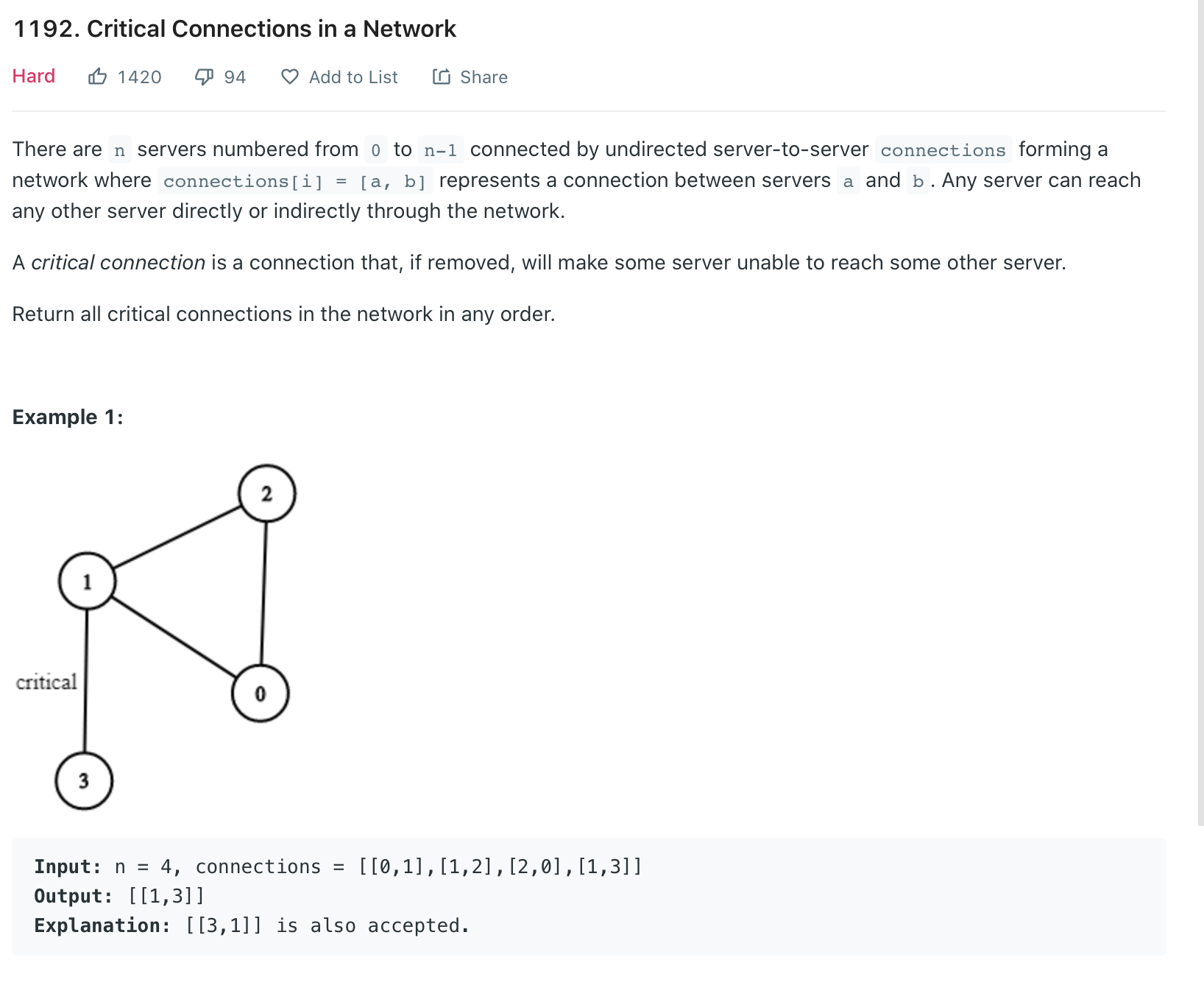
문제

n 개의 vertex를 가진 무방향 그래프가 있다. vertex간의 연결은 모두 이루어져있으며, 하나의 vertex에서 각각의 vertex까지 가는 경로가 최소 1가지이상은 존재한다.

여기서 edge하나를 제거했을 때, 그래프가 2개 이상으로 나눠지는 edge의 집합을 구하여라

라는 것이 문제였다.

난이도 Hard 문제

해결방법

맨 처음 DFS를 떠올렸다.
각각의 edge를 뺀 그래프에서 각 vertex간의 DFS를 실행하고, start vertex가 2개 이상이 된다면 그래프가 분리 된 것임을 알 수 있기 때문이다.

소스코드

class Solution {
    public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
        Graph graph = new Graph(n);
        return graph.findCriticalNum(connections);
    }
}

class Graph{
    int v;
    ArrayList<Integer>[] adjacent;
    ArrayList<List<Integer>> answer;
    
    public Graph(int v){
        this.v = v;
        adjacent = new ArrayList[v];
        for(int i=0; i<v; i++)
            adjacent[i] = new ArrayList<Integer>();
        
        answer = new ArrayList<>();
    }
    
    public void addEdge(int v, int w){
        adjacent[v].add(w);
        adjacent[w].add(v);
    }
    
    public boolean isOneDfs(){
        int union = 0;
        boolean[] visited = new boolean[v];
        for(int i=0; i<v; i++){
            if(union>=2) return false;
            if(!visited[i]){
                goDfs(i, visited);
                union++;
            }
        }
        if(union==1) return true;
        return false;
    }
    
    public void goDfs(int vertex,boolean[] visited){
        visited[vertex] = true;
        for(int next : adjacent[vertex]){
            if(!visited[next])
                goDfs(next,visited);
        }
    }
    
    public void cleanEdge(){
        for(int i=0; i<v; i++)
            adjacent[i] = new ArrayList<>();
    }
    
    public List<List<Integer>> findCriticalNum(List<List<Integer>> connections){
        for(int i=0; i<connections.size(); i++){
            List<List<Integer>> newConnection = new ArrayList<>(connections);
            newConnection.remove(i);
            cleanEdge();
            for(List<Integer> edge : newConnection){
                addEdge(edge.get(0),edge.get(1));
            }
            if(!isOneDfs()) answer.add(connections.get(i));
        }
        return answer;
    }
    
}

문제점

순조롭게 풀리는가 싶더니, Time Limit Exceed! 가 떳다.

음,, 아무래도 하나의 edge를 제거하고 처음부터 DFS를 돌린다는 점에서 시간이 오래 걸리는 것 이었다. 즉 $O(E*(V+E))$ 의 시간 복잡도를 가지게 되버리니 느릴 수 밖에 없었다.

해결방법 - Tarjan Algorithm

타잔이라는 사람이 개발해서 타잔 알고리즘이라는 것 같다.
타잔 알고리즘의 경우 SCC를 $O(|E|)$ 시간으로 짧게 구할 수 있다.
(이해 하기 어렵더라,,,)

따라서 SCC가 다른 경우의 edge가 존재하는 경우 추가 해주면 되는 문제 였다.

소스코드

import java.lang.*;

class Solution {
    static int time = 0;
    static List<Integer>[] network;
    static int[] lowestVertex; 
    static int[] discoveredTime;
    static boolean[] visited;
    static List<List<Integer>> critialConnections;

    public static List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {

        initialization(n);
        buildNetwork(connections);
        getCritialConnections(0, -1);

        return critialConnections;
    }

    public static void initialization(int n) {
        lowestVertex = new int[n];
        discoveredTime = new int[n];
        visited = new boolean[n];
        critialConnections = new ArrayList<>();

        network = new ArrayList[n];
        for(int i=0; i<n; i++) network[i] = new ArrayList<>();
    }

    public static void buildNetwork(List<List<Integer>> connections) {
        for(List<Integer> connection :connections) {
            network[connection.get(0)].add(connection.get(1));
            network[connection.get(1)].add(connection.get(0));
        }
    }


    public static void getCritialConnections(int current, int parent) {

        time++;
        lowestVertex[current] = time;
        discoveredTime[current] = time;
        visited[current] = true;

        for(int neighbor : network[current]) {
            if(neighbor == parent) continue;

            if(visited[neighbor] == false) { 

                getCritialConnections(neighbor, current);

                lowestVertex[current] = Math.min(lowestVertex[current], lowestVertex[neighbor]);


                if(lowestVertex[neighbor] > discoveredTime[current]) {
                    critialConnections.add(Arrays.asList(current, neighbor));
                }
            } else { 
                lowestVertex[current] = Math.min(lowestVertex[current], discoveredTime[neighbor]);
            }
        }
    }
}

해결

시간내에 해결하는 것 자체가 어려웠다.

난이도 (상)문제 확실!