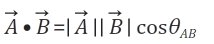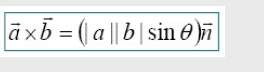[알고리즘] 계산 기하

600g (Kim Dong Geun)·2020년 4월 30일

공부를 하면서 쓰는 내용 이라 글이 지저분할 수 있습니다.

계산기하란?

점, 선, 다각형과 원 등 각종 기하학적 도형을 다루는 알고리즘을 게산 기하 알고리즘이라고 합니다. 라고 적혀있습니다. 흔히 Vector를 다뤄서 최적 알고리즘을 구하는 경우가 이에 해당합니다.

계산 기하의 도구들

위에서 벡터 사용한다고 했죠?
벡터 씁니다. 벡터에 대한 개념을 알아야 될 것 같아요.
2d Vector를 사용한다고 치면 자바는 벡터를 다음과 같이 사용할 수 있을것 같습니다.

public class Vector2D {

    public double x;
    public double y;
    
    public Vector2D() { }

    public Vector2D(double x, double y) {
        this.x = x;
        this.y = y;
    }

    public Vector2D(Vector2D v) {
        set(v);
    }

    public void set(double x, double y) {
        this.x = x;
        this.y = y;
    }

    public void set(Vector2D v) {
        this.x = v.x;
        this.y = v.y;
    }

    public void setZero() {
        x = 0;
        y = 0;
    }

    public double[] getComponents() {
        return new double[]{x, y};
    }

    public double getLength() {
        return Math.sqrt(x * x + y * y);
    }

    public double getLengthSq() {
        return (x * x + y * y);
    }

    public double distanceSq(double vx, double vy) {
        vx -= x;
        vy -= y;
        return (vx * vx + vy * vy);
    }

    public double distanceSq(Vector2D v) {
        double vx = v.x - this.x;
        double vy = v.y - this.y;
        return (vx * vx + vy * vy);
    }

    public double distance(double vx, double vy) {
        vx -= x;
        vy -= y;
        return Math.sqrt(vx * vx + vy * vy);
    }

    public double distance(Vector2D v) {
        double vx = v.x - this.x;
        double vy = v.y - this.y;
        return Math.sqrt(vx * vx + vy * vy);
    }

    public double getAngle() {
        return Math.atan2(y, x);
    }

    public void normalize() {
        double magnitude = getLength();
        x /= magnitude;
        y /= magnitude;
    }

    public Vector2D getNormalized() {
        double magnitude = getLength();
        return new Vector2D(x / magnitude, y / magnitude);
    }

    public static Vector2D toCartesian(double magnitude, double angle) {
        return new Vector2D(magnitude * Math.cos(angle), magnitude * Math.sin(angle));
    }

    public void add(Vector2D v) {
        this.x += v.x;
        this.y += v.y;
    }

    public void add(double vx, double vy) {
        this.x += vx;
        this.y += vy;
    }

    public static Vector2D add(Vector2D v1, Vector2D v2) {
        return new Vector2D(v1.x + v2.x, v1.y + v2.y);
    }

    public Vector2D getAdded(Vector2D v) {
        return new Vector2D(this.x + v.x, this.y + v.y);
    }

    public void subtract(Vector2D v) {
        this.x -= v.x;
        this.y -= v.y;
    }

    public void subtract(double vx, double vy) {
        this.x -= vx;
        this.y -= vy;
    }

    public static Vector2D subtract(Vector2D v1, Vector2D v2) {
        return new Vector2D(v1.x - v2.x, v1.y - v2.y);
    }

    public Vector2D getSubtracted(Vector2D v) {
        return new Vector2D(this.x - v.x, this.y - v.y);
    }

    public void multiply(double scalar) {
        x *= scalar;
        y *= scalar;
    }

    public Vector2D getMultiplied(double scalar) {
        return new Vector2D(x * scalar, y * scalar);
    }

    public void divide(double scalar) {
        x /= scalar;
        y /= scalar;
    }

    public Vector2D getDivided(double scalar) {
        return new Vector2D(x / scalar, y / scalar);
    }

    public Vector2D getPerp() {
        return new Vector2D(-y, x);
    }

    public double dot(Vector2D v) {
        return (this.x * v.x + this.y * v.y);
    }

    public double dot(double vx, double vy) {
        return (this.x * vx + this.y * vy);
    }

    public static double dot(Vector2D v1, Vector2D v2) {
        return v1.x * v2.x + v1.y * v2.y;
    }

    public double cross(Vector2D v) {
        return (this.x * v.y - this.y * v.x);
    }

    public double cross(double vx, double vy) {
        return (this.x * vy - this.y * vx);
    }

    public static double cross(Vector2D v1, Vector2D v2) {
        return (v1.x * v2.y - v1.y * v2.x);
    }

    public double project(Vector2D v) {
        return (this.dot(v) / this.getLength());
    }

    public double project(double vx, double vy) {
        return (this.dot(vx, vy) / this.getLength());
    }

    public static double project(Vector2D v1, Vector2D v2) {
        return (dot(v1, v2) / v1.getLength());
    }

    public Vector2D getProjectedVector(Vector2D v) {
        return this.getNormalized().getMultiplied(this.dot(v) / this.getLength());
    }

    public Vector2D getProjectedVector(double vx, double vy) {
        return this.getNormalized().getMultiplied(this.dot(vx, vy) / this.getLength());
    }

    public static Vector2D getProjectedVector(Vector2D v1, Vector2D v2) {
        return v1.getNormalized().getMultiplied(Vector2D.dot(v1, v2) / v1.getLength());
    }

    public void rotateBy(double angle) {
        double cos = Math.cos(angle);
        double sin = Math.sin(angle);
        double rx = x * cos - y * sin;
        y = x * sin + y * cos;
        x = rx;
    }

    public Vector2D getRotatedBy(double angle) {
        double cos = Math.cos(angle);
        double sin = Math.sin(angle);
        return new Vector2D(x * cos - y * sin, x * sin + y * cos);
    }

    public void rotateTo(double angle) {
        set(toCartesian(getLength(), angle));
    }

    public Vector2D getRotatedTo(double angle) {
        return toCartesian(getLength(), angle);
    }

    public void reverse() {
        x = -x;
        y = -y;
    }

    public Vector2D getReversed() {
        return new Vector2D(-x, -y);
    }

    @Override
    public Vector2D clone() {
        return new Vector2D(x, y);
    }

    @Override
    public boolean equals(Object obj) {
        if (obj == this) {
            return true;
        }
        if (obj instanceof Vector2D) {
            Vector2D v = (Vector2D) obj;
            return (x == v.x) && (y == v.y);
        }
        return false;
    }

    @Override
    public String toString() {
        return "Vector2d[" + x + ", " + y + "]";
    }
}

출처: https://gist.github.com/gunvirranu/6816d65c0231981787ebefd3bdb61f98
github에서 굉장히 좋은 vector2d 예제를 찾아서 이렇게 올립니다.
실제로 c++과는 다르게 자바는 연산자 오버로딩이 없기 때문에 method로 구현하는 것을 알 수 있습니다.

벡터의 내적과 외적

내적

벡터의 내적은 위와 같이 구성된다. ~~A*B Cos세타 알지?~~
내적으로 할 수 있는 일은 3가지 정도가 있다

벡터의 사이각 구하기
Theta = acos(vector1,vector2);
자바에서 Math 클래스를 통해서 Acos을 구할 수 잇다.
벡터의 직각여부 확인
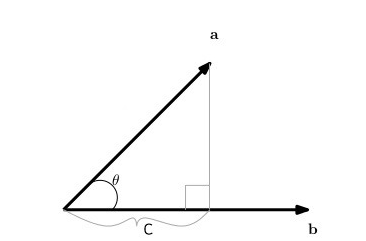
vector1,vector2를 내적한 값이 0 이면 그 각은 +90,-90도가 되겠죠?
벡터의 사영
비교하는 두 벡터 중에 한 벡터를 다른 한벡터로 내려꽃았을때 값이라고 보면된다.
(위그림에서 a벡터 값이 (c,y)라면 b에 사영시켰을 때 (c,0)이라고 볼 수 있을 것)

외적

벡터의 외적은 위와 같이 표현할 수 있다.
벡터의 외적으로 할 수 있는 일은 다음과 같다.

면적 구하기 = $|vectorA * vector B |$
벡터의 방향 판별
각각의 벡터 값이 음수이냐 양수이냐에 따라서 벡터의 상대적인 위치를 알 수 있게 된다.
$vectorA * vectorB = a_x*b_y-a_y*b_x$ 로 볼수 있다.
- 양수일 경우
vectorB가 A보다 시계방향으로 위치해있다.
- 음수일 경우
vectorB가 A보다 반시계방향에 위치해있다.

교차와 거리, 면적

두 직선의 교차여부를 확인하는 것은 계산 기하 문제의 단골 주제라고 한다. ~~난 모르겠다~~

직선과 직선의 교차

$a+p*b = c+q*d$

위 공식을 기억하자 위 연립 방정식을 풀면 직선이 교차 하는 것을 알 수 있다.

이 연립 방정식을 방정식 p에 대해서 풀게 된다면

$a_x+p*b_x =c_x+q*d_x$
$a_y+p*b_y = c_y+q*d_y$

따라서 위 연립 방정식을 정리하면

$p=(c-a)*d/b*d$

가 되는 것을 알 수 있다.

선분과 선분의 교차
한 직선 위에 두 선분이 있을때, 이 선분들의 관계는 넷 중 하나임을 알 수 있습니다

두 선분이 서로 겹치지 않음
두 선분이 한 점에서 닿음
두 선분이 겹쳐짐
한 선분이 다른 선분 안에 포함됨.

boolean lineInterSection(Vector2D a,Vector2D ,vector2D c,vector2D d){
	double bet = (b.minus(a)).cross(d.minus(c));
    if(Math.abs(bet)< 0.000000001) return false;
    else return true;
}

선분과 선분의 교차 : 교차점이 필요 없을 때
교차점을 구할 필요 없이 두 선분의 교차 여부를 확인하기만 하는 거라면 간단한 방법이 존재!

선분과 선분사이의 각도를 구하는 함수 이용

ab = ccw(a,b,c) * ccw(a,b,d);
cd = ccw(a,b,c) * ccw(c,d,b);
if(ab==0 && cd ==0){
	if(b < a) swap(a,b);
    if(d < c) swap(c,d);
    return !(b<c || d<a);
  }
return ab<=0 && cd<=0;

600g (Kim Dong Geun)

수동적인 과신과 행운이 아닌, 능동적인 노력과 치열함

이전 포스트

2020 Naver HackDay 선정 후기

다음 포스트