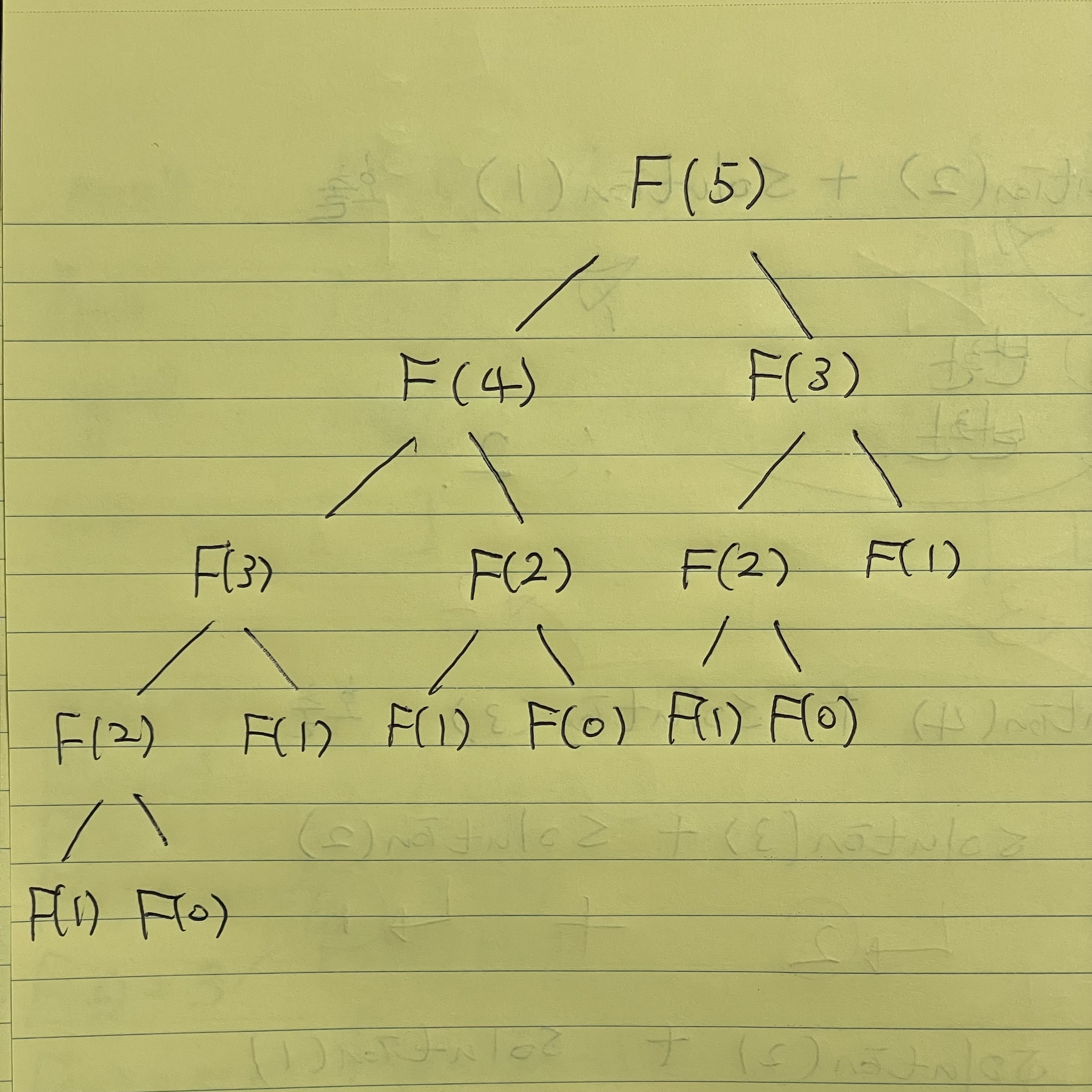[프로그래머스] 피보나치 수 - 파이썬

링크: https://school.programmers.co.kr/learn/courses/30/lessons/12945

문제 설명

피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다.

예를들어

• F(2) = F(0) + F(1) = 0 + 1 = 1
• F(3) = F(1) + F(2) = 1 + 1 = 2
• F(4) = F(2) + F(3) = 1 + 2 = 3
• F(5) = F(3) + F(4) = 2 + 3 = 5

와 같이 이어집니다.

2 이상의 n이 입력되었을 때, n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴하는 함수, solution을 완성해 주세요.

제한 사항

• n은 2 이상 100,000 이하인 자연수입니다.

입출력 예

n	return
3	2
5	5

입출력 예 설명

피보나치수는 0번째부터 0, 1, 1, 2, 3, 5, ... 와 같이 이어집니다.

---

문제풀이

문제 이해하기:
피보나치 수는 첫째 및 두 번째 항이 1이고, 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열.

목표: 2 이상의 n 이 주어졌을 때, n 번째 피보나치 수를 1234567로 나눈 나머지값을 return

첫 번째 풀이(재귀함수, 시간초과):

피보나치 수열의 방식을 좀 더 쉽게 이해하기 위해 그림으로 표현해봤다.

각 항이 몇 번 사용됐는지 세어보면 다음과 같다.

• F(5): 1번
• F(4): 1번
• F(3): 2번
• F(2): 3번
• F(1): 5번
• F(0): 3번

같은 항에 대해 여러번 반복 계산한다는 점을 활용하여 간단하게 재귀함수로 피보나치 수열을 구현할 수 있다.

코드

def solution(n):
    if n <= 2:
        return 1
    else:
        return (solution(n-1) + solution(n-2)) % 1234567

• 하지만 이 경우에는 각 호출에서 두 개의 하위 호출을 수행하며 불필요한 연산이 반복되기 때문에 시간복잡도가 거의 $O(2^n)$이다.
• 그래서 해당 코드로 결과를 보면 시간 초과가 발생한다.

두 번째 풀이(반목문, 통과):

시간 초과를 해결하기 위해 재귀함수 대신 반복문으로 바꿨고, 피보나치 수의 연산 결과를 딕셔너리 형태로 저장해줬다.

• 반복문을 사용하는 경우 n 번의 연산만 하면 되기 때문에 시간 복잡도를 $O(n)$ 까지 줄일 수 있다.

최종코드

def solution(n):
    fibo = {0: 0, 1: 1}
    
    for i in range(2, n+1):
        fibo[i] = fibo[i-1] + fibo[i-2]
    
    return fibo[n] % 1234567