[알고리즘] Binary Search Trees_2편 ( 삽입, 삭제 )

1. 이진탐색트리 삽입 ( Binary search Tree Insert )

• 새로운 수를 삽입함에 있어, 기존 노드의 위치를 변경 하지 않는다.
  => 작은 수는 좌측 큰 수는 오른쪽 서브트리에 존재한다 점을 이용하여, 비교 & 삽입하면 된다.

< Pseudo Code >

1. T는 Binary search Tree // z는 삽입 할 노드를 의미.

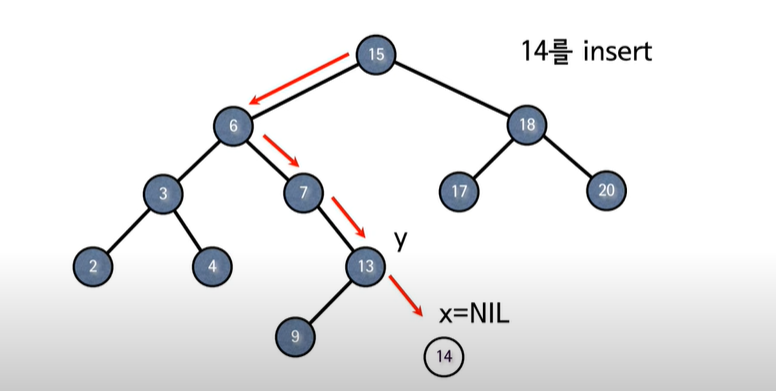
2. X는 트리의 루트에서 시작하고, Y는 항상 X의 뒤에 있기에 NULL로 시작

3. X = NULL이 될 때까지 루프를 돌린다. (= Y는 X의 뒤에 있기에, X가 NULL이 되면 Y의 자식의 위치에 Z를 삽입한다는 개념)

4. Z값과 X값을 비교하여 크면 오른쪽, 작으면 좌측으로 이동 => 아래로.

5. P[Z] <- Y는 삽입 할 Z의 부모가 Y라고 포인팅.

6. IF Y = NULL 이라는 말은, X의 이동이 없다는 의미 즉, 트리가 비어있다.
   그런경우, 트리의 루트 노드에 Z를 삽입하고
   그렇지 않은 경우, 작으면 Y의 왼쪽, 크면 오른쪽에 Z를 삽입하고 마무리.

'시간 복잡도 = O(h)'

2. 이진탐색트리 삭제 ( Binary search Tree DELETE )

• 삭제는 사전작업으로 검색을 수반한다.
• 삭제 카테고리에서는 오로지 삭제만을 다뤄 보려 한다.
• 삭제를 위한 방법론은 3가지로 분류해서 일반적으로 접근한다.

case 1. 자식노드가 없는 경우

• 자신을 삭제해도 노드의 변경이 필요 없기에, 단순히 삭제가 가능하다

case 2. 자식 노드가 1개인 경우

• 자신의 자식노드를 삭제 될 자신의 노드 위치로 이동시킨다.

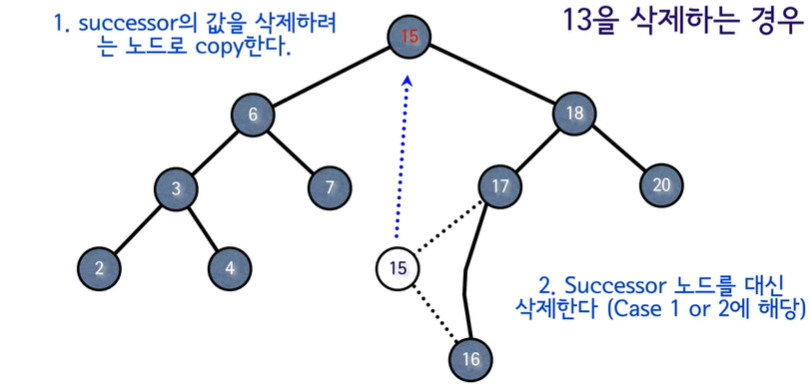
case 3. 자식 노드가 2개인 경우

• 자식 노드가 2개인 경우, 삭제 연산이 일어날 경우 부모 노드였던 z라는 삭제 될 노드를 대신 할 노드를 찾아서 빈 자리를 보충 해야한다.
• 하지만, 이진탐색트리가 가지는 특징을 존중하며 삭제가 이루어져야 하기 때문에 가장 효율적인 대체 노드를 고려 해야한다.
• 자신과 가장 가까운 수인 predecessor || Successor 를 대체 노드로 선택하는 경우 기존 트리의 형태 유지가 가능하다.

< Delete Pseudo Code >

• 1. T는 Binary search Tree // z는 삭제 할 노드를 의미.
• 2. [ 2 ~ 4 ] 자식 노드가 0개 또는 1개라면 z를 y가 가르키게 하고,
     그렇지 않다면, z의 successor를 y가 가르키게 한다.
     => y는 궁극적으로 우리가 삭제 할 노드.
     
• 3. [ 4~ 13] 노드 Y를 삭제하는 과정, Y =Z 일때 즉, Y의 자식은 0 OR 1개이다.
  • 3-1
    left [y] != NULL 이라면, X를 왼쪽 자식으로 지정.
    left [y] == NULL 이라면, X를 오른쪽 자식으로 지정.
  • 3-2
    X != NULL 이라면, Y를 삭제하고 X를 Y자리로 이동.
  • 3-3
    Y의 부모가 NULL 이라면 => Y가 'ROOT' 라는 말이다.
    즉 Y를 삭제하면, X가 이 트리의 새로운 루트 노드가 된다.
    Y의 부모가 있을 때, Y가 왼쪽 자식이라면 X를 왼쪽으로 배치.

• 4. Y != Z라는 말은 자식노드가 2개, 즉 CASE 3를 의미한다.
     - 이 경우 Successor의 값을 z의 자리로 이동.

     시간 복잡도 : O(h) 이지만, 트리의 높이가 O(n) 인 최악의 경우가 존재.