[Algorithm] HW4

	Describe linear median finding algorithm. Show that its time complexity is Θ(n).

선형 중앙값 찾기 알고리즘을 설명한다. 시간 복잡도가 Θ(n)임을 보여준다.

선형 중앙값 알고리즘이란 목록을 반복하고 각 요소를 피벗값과 비교하여 값 집합의 중앙값을 찾는 방법이다.

1. 목록에서 피벗 값을 선택합니다.
2. 목록을 피벗 값보다 작은 요소와 피벗 값보다 큰 요소의 두 그룹으로 나눕니다.
3. 피벗 값이 중앙값이면 반환합니다.
4. 피벗 값이 중앙값보다 작으면 피벗보다 큰 요소 그룹에서 알고리즘을 반복합니다.
5. 피벗 값이 중앙값보다 크면 피벗보다 작은 요소 그룹에서 알고리즘을 반복합니다.
   선형 중앙값 찾기 알고리즘의 시간 복잡도는 Θ(n)이며, 여기서 n은 입력 목록의 크기입니다.

이는 알고리즘이 중앙값을 찾기 위해 목록의 각 요소를 한 번씩 반복해야 하기 때문입니다. 분할 단계는 최악의 경우 O(n) 시간이 걸리지만 알고리즘이 재귀적이므로 각 분할은 한 번만 처리하면 되므로 총 시간 복잡도는 Θ(n)입니다.

  In hashing function, why the coefficient a should not be 0?

해싱 함수에서 계수가 a가 0이 아니여야 하는 이유는 무엇인가?

a가 0이면 해시 함수가 h(k) = b % m이 되기 때문이다.

b가 모든 키에 대해 동일하면 모든 키는 해시 테이블의 동일한 슬록으로 해시되며 성능 저하의 원인이 된다.

0이 아닌 계수a를 사용하면 해시 테이블 전체에 키를 보다 균등하게 분배해 충동의 위험을 방지한다.

Collision(충돌현상) : 서로 다른 두개이상의 레코드가 같은 주소를 갖는 현상이다.

  Read chapter 8.4. Solve example 8.1 in the chapter.

8.1 만약 키가 균일하게 분포되어 있고 n=2m이라면, 실패한 검색은 각각 2m/m=2번의 비교만 필요하고, 성공한 검색은 평균 비교 횟수가 다음과 같다.

$\frac{2m}{2m}+\frac12=\frac32$

키가 균일하게 분포되어 있으면 검색시간은 매우 적다. 각 키가 서로 다른 바구니로 각각 해시될 확률이 거의 같다고 가정한다.

만약 n개 키와 m개의 바구니가 있고, 각 키가 서로 다른 바구니로 각각 해시될 확률이 거의 같다고 가정하면 한개의 바구니에 최소한 k개 키가 들어있을 확률은 다음보다 작거나 같다.

•      Basic quick sort

  기본 퀵 정렬

Pivot X = A[0] or A[n-1]
피벗 X = A[0] 또는 A[n-1]

•      Intelligent quick sort

  지능형 퀵 정렬

Pivot X = median of A
피벗 X = A의 중앙값

•      Paranoid quick sort

  편집증 빠른 정렬

Pivot X = E(Good choice)
피벗 X = E(좋은 선택)

•      Tuple sort

  튜플정렬
  1) The month comes first, and the date second
  월이 먼저 오고 날짜가 두 번째로 온다.
  2) The date comes first, and the month second
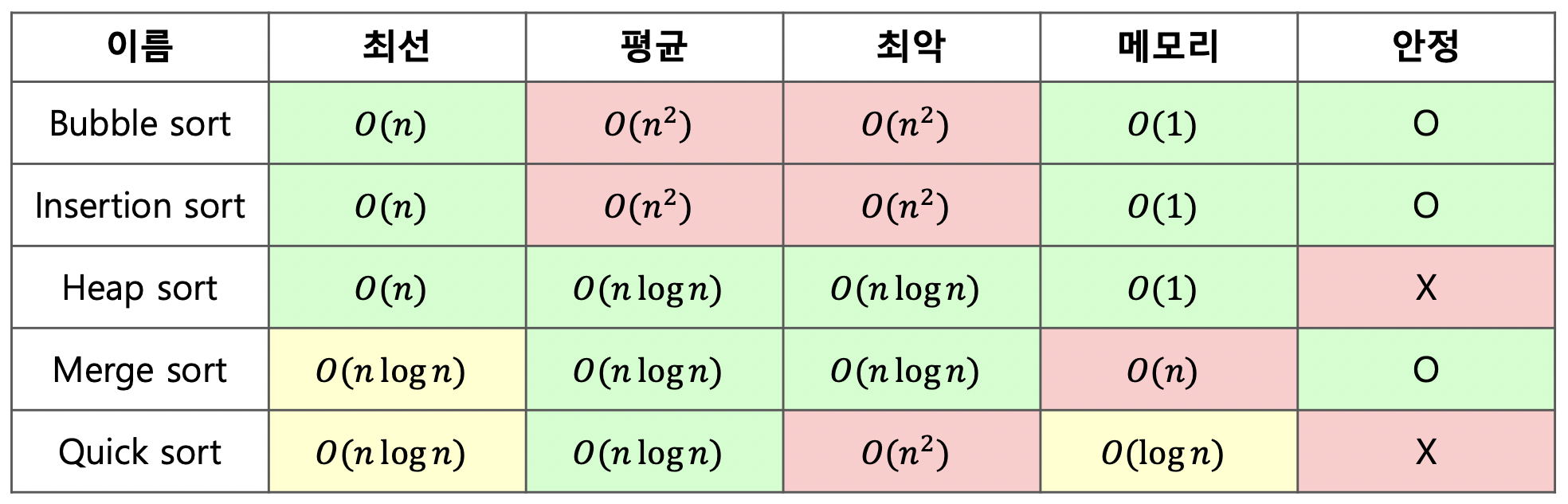
  날짜가 먼저오고 월이 두 번째로 온다.

          Compare the sorting algorithms

  정렬 알고리즘 비교한다.