Solve the exercise problem 14 of the chapter 7.
Q14. 합병정렬 알고리즘에서 레코드의 저장 횟수를 기준으로 할 때 시간복잡도는 대략 T(n) = 2n lg n 이됨을 증명하시오.
MergeSort
합병정렬(MergeSort)은 배열을 정확히 반으로 분할하여 각각 따로 정렬한 뒤 합병하여 정렬된 배열을 만들 수 있다. 이런 식으로 게속 반으로 분할하다 보면 언젠간 원소가 하나인 배열이 될 텐데, 하나짜리 배열은 물어보나마나 정렬된 배열일 것이다.
원소가 n개인 배열은 다음과 같은 절차로 합병정렬을 적용한다.
- 분할
배열을 반으로 분할한다. 분할한 배열의 원소는 각각 n/2개이다.- 정복
분할한 배열을 각각 따로 정렬한다.
(배열에 원소가 2개 이상이면 합병정렬을 재귀 호출하여 정렬한다.)- 취합
정렬한 두 배열을 합병하여 정렬한다.
문제의 레코드의 저장 횟수는 두개의 분할한 부분을 정렬한 후에 합치는 과정에서 발생한다.
전체의 원소가 n개인 배열에서 분할해 각 부분의 크기가 n/2이라고 할때, 부분을 정렬하는 과정에서 각 부분마다 T(n/2)만큼의 시간이 소요된다.
전체의 시간복잡도는 2 T(n/2)가 된다.
분할과정에서 각각의 부분 배열을 생성하는 데 n번의 레코드 저장이 필요하며, 총 2n번의 레코드가 저장된다.
합병 과정에서 두 부분 배열을 비교할 때, 더 작은 원소를 새로운 배열에 저장하고 두 부분 배열 중 하나가 모두 사용되면, 나머지 부분 배열의 원소들을 새로운 배열에 복사한다. 이 과정에서 새로운 배열에 저장하는 레코드의 수는 최대 n개가 된다.
총 분할과정에서의 2n번과 합병과정에서 n번이 걸리면서 3n의 시간복잡도를 가진다.
전체적인 시간복잡도는 T(n) = 2T(n/2) + 3n 가된다.
재귀적으로 풀었을 때 T(n) = nT(1) + n lg n × 2 가 되며 상수를 제외하면 최종적으로 합병 정렬의 시간 복잡도는 대략 T(n) = 2n lg n으로 구할 수 있다.
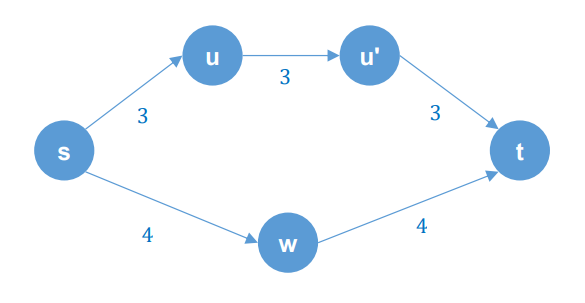
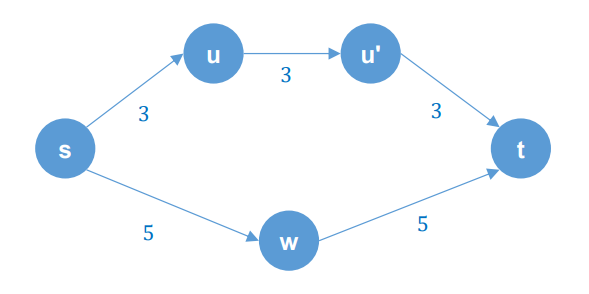
Can you improve this Bi-Directional Search algorithm? Describe the procedure. 양방향 검색은 그래프 탐색 알고리즘으로, 출발 노드와 목적지 노드에서 동시에 시작하여 최단 경로를 찾는 알고리즘입니다. 이 알고리즘은 출발지에서 목적지로의 검색과 목적지에서 출발지로의 검색 두 가지를 동시에 실행합니다. 이 두 검색은 가장 짧은 경로의 중간 지점에서 만납니다.
다음은 양방향 검색 알고리즘의 성능을 향상시키는 몇 가지 방법입니다.
휴리스틱 함수 사용: 휴리스틱 함수는 노드와 목표 노드 사이의 거리를 추정합니다. 휴리스틱 함수를 사용하면 검색을 목표로 안내하여 탐색하는 노드 수를 줄일 수 있습니다. 휴리스틱 기반 검색 알고리즘 예시로는 A* 알고리즘이 있습니다.
검색 공간 제한: 최단 경로가 아닌 노드를 제거하여 검색 공간을 줄일 수 있습니다. 이를 위해 우선순위 큐를 사용하는 Dijkstra 알고리즘의 변형을 사용하여 양방향 검색을 수행할 수 있습니다. 이 변형된 Dijkstra 알고리즘은 출발지에서 각 노드까지의 최단 경로 하한과 목적지에서 각 노드까지의 최단 경로 하한을 계산합니다. 하한의 합이 현재 최단 경로 길이보다 큰 노드는 제거할 수 있습니다.
더 효율적인 데이터 구조 사용: 해시 테이블이나 우선순위 큐와 같은 더 효율적인 데이터 구조를 사용하면 알고리즘의 시간 복잡도를 줄일 수 있습니다.
병렬 처리 사용: 두 검색을 병렬로 실행하여 최단 경로를 찾는 시간을 단축할 수 있습니다.
검색 공간 축소 기법 적용: 알파-베타 가지치기, 전이 테이블, 반복 깊이 우선 탐색 등 검색 공간 축소 기법을 적용하여 검색 공간을 줄이고 알고리즘 성능을 개선할 수 있습니다.
