Priority Queue & Heap
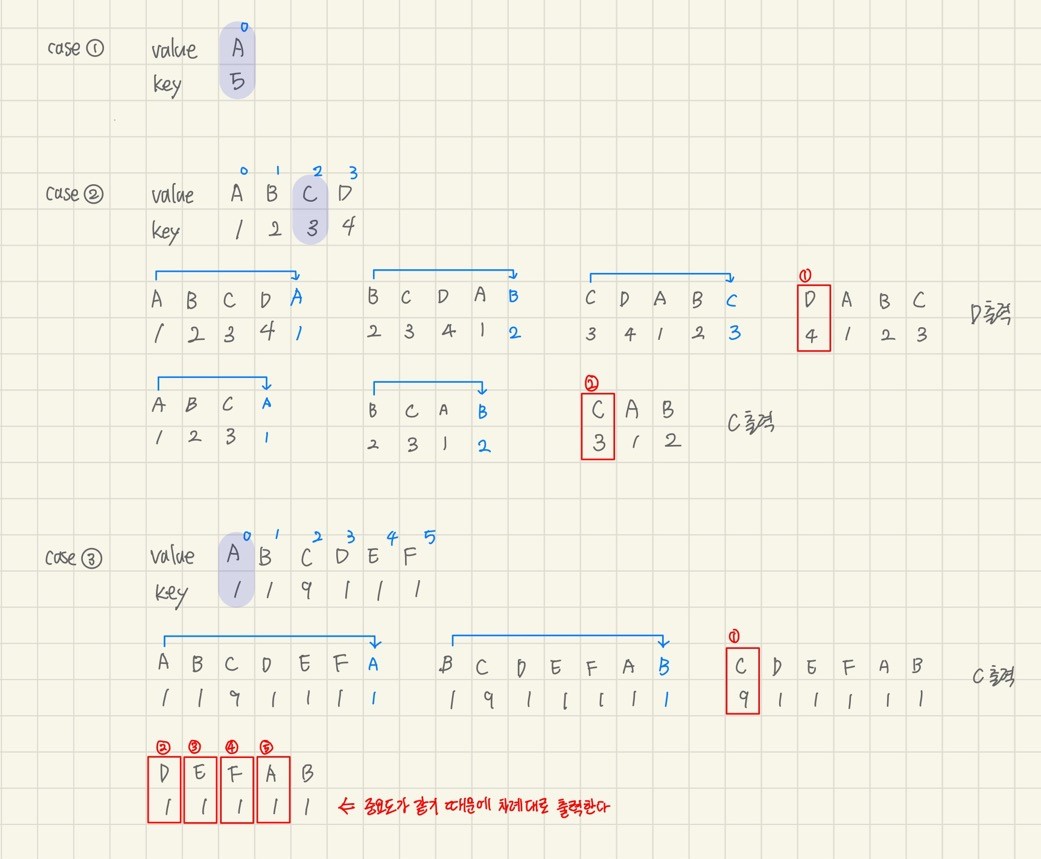
Priority Queue(우선순위큐)
- 데이터들이 우선순위(priority)를 가지고 있어 우선순위가 가장 높은 데이터가 먼저 출력된다.
- 우선순위 큐의 구현이 가장 효율적인 구조는 힙이다.
우선순위 큐 배열과 연결리스트, 힙으로 구현하였을 때의 삽입과 삭제의 시간 복잡도를 구해 비교한다.
O(n)과 O(log2n)은 큰 차이를 가진다.
n이 1024일 때 O(n)알고리즘은 1024초가 소요되고 O(log2n)알고리즘은 10초가 소요된다.
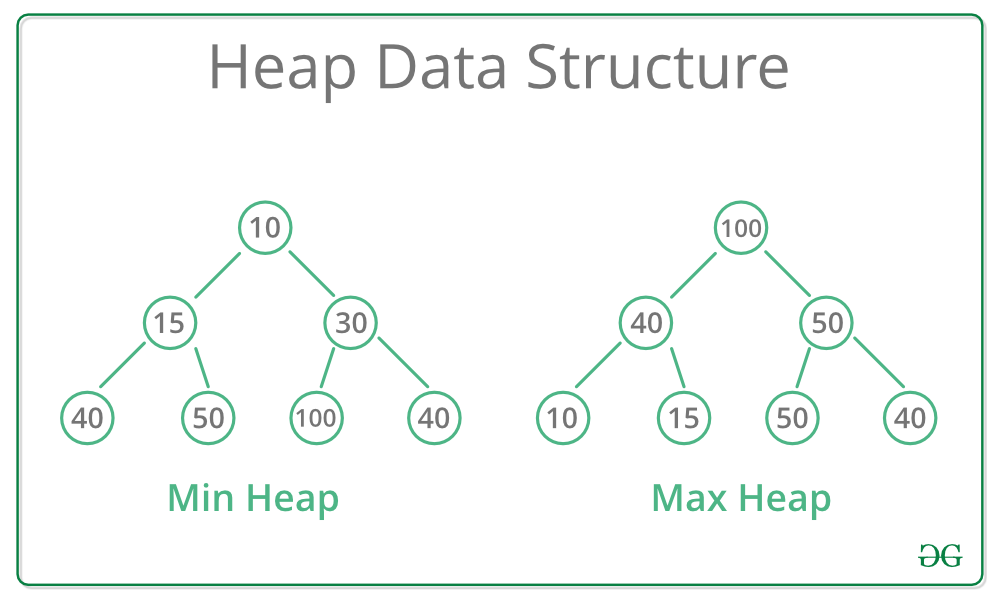
Heap(힙)
- 완전 이진트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조
- 반 정렬 상태 => 우선순위 큐 구현
- 큰 값이 상위 레벨 작은 값이 하위레벨에 위치한다는 정도의 느슨한 정렬 상태(삭제 연산에서 가장 큰 값을 찾기 위함->전체 정렬 필요 X)
- 힙은 배열을 사용하여 구현한다.
key(부모 노드의 키 값) >= key(자식 노드의 키 값)
- 최대 힙(max Heap)
부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리- 최소 힙(min Heap)
부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진트리왼쪽 자식의 인덱스 = 부모의 인덱스2
오른쪽 자식의 인덱스 = 부모의 인덱스2+1
부모의 인덱스 = 자식의 인덱스/2
우선순위 큐 프로그래밍
STL의 우선순위 큐를 사용한 정렬
- push() : 삽입함수
- top() : 우선순위 높은 항목 삭제X 반환O
- pop() : 우선순위 높은 항목 삭제O 반환X
- size() : 요소의 개수
- empty() : 비어있는지 여부
1) STL의 우선순위 큐 사용을 위해 헤더파일 queue를 선언한다.
#include <queue>
2) 최대 힙을 사용한 큐 객체 (less than operator = 가장 값이 큰 항목부터 출력)
priority_queue <int> maxHeap;
3) 최소 힙을 사용한 큐 객체 (greater than operator = 가장 값이 작은 항목부터 출력)
priority_queue <int, vector<int>, greater<int>> minHeap;#include <iostream> #include <queue> #include <functional> using namespace std; void MaxHeapSorting(int a[], int n) { //STL의 우선순위를 사용한 최대 힙 정렬(내림차순) priority_queue <int> maxHeap; for (int i = 0; i < n; ++i) //요소를 우선순위 큐에 삽입한다. maxHeap.push(a[i]); for (int i = 0; i < n; i++) { //maxHeap를 사용하여 내림차순으로 정렬하기 위한 반복문 a[i] = maxHeap.top(); maxHeap.pop(); } } void MinHeapSorting(int a[], int n) { //STL의 우선순위를 사용한 최소 힙 정렬(오름차순) priority_queue<int, vector<int>, greater<int>>minHeap; for (int i = 0; i < n; ++i) minHeap.push(a[i]); for (int i = 0; i < n; ++i) { //maxHeap를 사용하여 오름차순으로 정렬하기 위한 반복문 a[i] = minHeap.top(); minHeap.pop(); }
힙정렬을 통해 우선순위 큐 구현(STL 사용X)
#include <iostream> #define MAX_ELEMENT 200 using namespace std; //힙에 저장할 노드 클래스 class HeapNode { //하나의 노드 int key; public: HeapNode(int k = 0) : key(k) {} //생성자 void setKey(int k) { key = k; } int getKey() { return key; } void display() { cout << key << endl; } }; //최대 힙 클래스 구현 class MaxHeap { //최대 힙 HeapNode node[MAX_ELEMENT]; //HeapNode를 요소로 가지는 배열 int size; //힙의 현재 요소의 개수 public: MaxHeap() :size(0){} //생성자 bool isEmpty() { return size == 0; } bool isFull() { return size == MAX_ELEMENT; } //부모노드와 자식노드 구하기(참조자) HeapNode& getParent(int i) { return node[i / 2]; } //부모노드 HeapNode& getLeft(int i) { return node[i * 2]; } //왼쪽 자식노드 HeapNode& getRight(int i) { return node[i * 2 + 1]; } //오른쪽 자식노드 void insert(int key) { // 삽입함수 if (isFull()) return; int i = ++size; //증가된 힙 크기의 위치에서 시작한다. 추가한 노드의 위치에서 시작한다. while (i != 1 && key > getParent(i).getKey()) { //루트노드가 아니고, 부모노드의 키값보다 크면, node[i] = getParent(i); //부모노드 내린다. i /= 2; //i = i / 2 부모노드의 부모노드 위치로 이동한다. } node[i].setKey(key); //최종 위치 } HeapNode remove() { //가장 우선순위가 높은 값 삭제 if (isEmpty()) return NULL; HeapNode item = node[1]; //루트노드(삭제할 노드) HeapNode last = node[size--]; //힙의 마지막 노드 int parent = 1; //루트와 마지막 노드를 먼저 바꾸고 => 마지막 노드가 루트로 이동하여 생각 int child = 2; //루트노드의 왼쪽자식노드의 위치 while (child <= size) { //자식노드들 중 더 큰 자식노드를 찾는다. if (child < size && getLeft(parent).getKey() < getRight(parent).getKey()) child++; //오른쪽이 더 크기 때문에 부모와 바꿀 값을 +1해준다. 아닐경우 왼쪽값인 child 그대로 사용 if (last.getKey() >= node[child].getKey()) break; //마지막 노드가 위에서 나온 자식보다 크면 이동이 완료! //마지막 노드가 위에 나온 자식보다 작으면 한 단계 아래로 이동 node[parent] = node[child]; parent = child; child *= 2; //child = child * 2 } node[parent] = last; //마지막노드를 최종 위치에 저장 return item; //루트노드 반환 } HeapNode find() { return node[1]; } //가장 우선순위가 높은 값 반환 }; void Max_Heapify(int a[], int n) { MaxHeap h; for (int i = 0; i < n; i++) { h.insert(a[i]); } //삭제시 가장큰 원래의 루트노드가 반환된다. //오름차순으로 정렬하기 위한 삭제한 항목을 배열의 끝부터 앞으로 채워나간다. for (int i = n - 1; i >= 0; i--) { a[i] = h.remove().getKey(); } } int main() { MaxHeap heap; int data[10]; for (int i = 0; i < 10; i++) data[i] = rand() % 100; cout << "정렬하기 이전" << endl; for (int i = 0; i < 10; i++) { cout << data[i] << " "; } Max_Heapify(data, 10); cout << endl; cout << "정렬한 이후" << endl; for (int i = 0; i < 10; i++) { cout << data[i] << " "; } cout << endl; }
문제풀이
백준 1966 - 프린터 큐
문제설명
입력
출력
코드설명
#include <iostream> #include <fstream> #include <queue> using namespace std; int main() { int testcase; ifstream fin("Prob_1966.txt"); fin >> testcase; for (int n = 0; n < testcase; n++) { //N : 문서의 개수 //M : 몇 번째에 놓여 있는지 int N, M; fin >> N >> M; //queue_data : 문서 우선순위와 문서 위치(index) queue <pair<int, int>> queue_data; //priorityqueue_data : 문서들의 우선순위 priority_queue <int> priorityqueue_data; for (int i = 0; i < N; i++) { int priority; fin >> priority; queue_data.push(make_pair(priority, i)); //문서 우선순위, 문서 위치(index) priorityqueue_data.push(priority); //우선순위 } while (priorityqueue_data.size()) { //temp_priority:출력중에 사용한 priority int temp_priority = queue_data.front().first; //변수temp_priority에 pair첫번째 값 복사 int m = queue_data.front().second; //변수m에 pair두번째 값 복사 queue_data.pop(); //해당 문서를 출력한다. if (priorityqueue_data.top() == temp_priority) { // if (m == M) { cout << N - priorityqueue_data.size() + 1 << endl; break; } priorityqueue_data.pop(); } else queue_data.push(make_pair(temp_priority, m)); } } fin.close(); return 0; }
백준 1655 - 가운데를 말해요
문제설명
입력
출력
STL queue에서는 탐색이 불가능하기 때문에 가운데 값까지 pop()을 반복한다.
코드설명
#include <iostream> #include <queue> using namespace std; int main() { //N 외치는 정수의 총개수 //n 외친 정수의 개수 //num 외친 정수 int N, n; cin >> N; //queue_data : queue <int> queue_data; //priorityqueue_data : 우선순위가 정수의 크기임으로 자료형을 추가하지 않고, 최소힙 정렬 //value값과 인데스값을 가진다. priority_queue <pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> priorityqueue_data; for (int i = 0; i < N; i++) { int num; cin >> num; //백준이가 외친 정수값num , 우선순위큐에서 num의 index값 priorityqueue_data.push(make_pair(num, i)); n++; while (N--) { //n이 짝수 if (n % 2 == 0) { } //n이 홀수( n % 2 == 1 ) else { } } } return 0; }