BinarySearchTree
BinarySearchTree(이진탐색트리)
탐색이란?
우리의 일상생활에서 많이 사용되는데
전화번호부에서 전화번호를 찾거나,
사전에서 단어를 검색하고,
인터넷 쇼핑몰에서 내가 원하는 물건을 찾는 작업
이진탐색트리(BST, Binary Search Tree)란?
이진트리 기반의 탐새글 위한 자료구조로 효율적인 탐색 작업을 위한 자료구조이다.
- 모든 노드는 유일한 키를 가진다.
- 왼쪽 서브트리의 키들은 루트의 키보다 작다.
- 오른쪽 서브트리의 키들은 루트의 키보다 크다.
- 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.
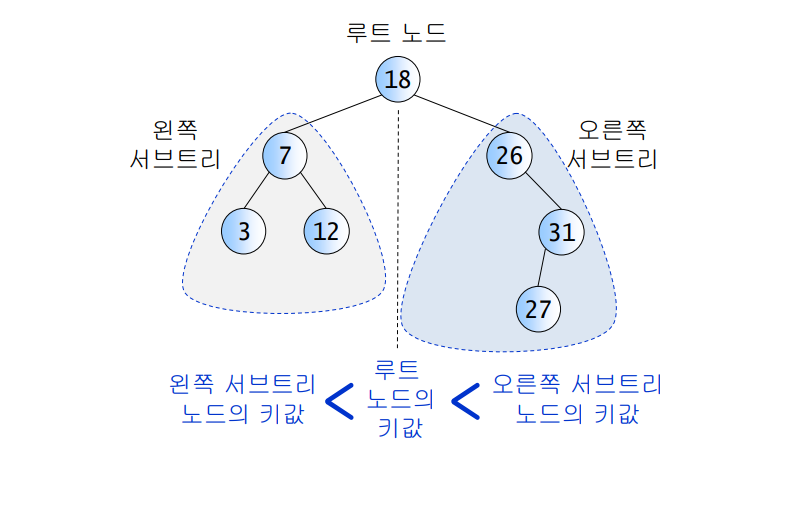
key(왼쪽서브트리) ≤ key(루트노드) ≤ key(오른쪽서브트리)
이진탐색를 중위순회하면 오름차순으로 정렬된 값을 가진다.
이진탐색트리 프로그래밍
탐색연산
search(key) : 키 값이 key인 노드를 찾아 반환한다.
- 루트노드부터 시작해 서브트리의 key를 키 값으로 갖는 노드를 검색한다.
- 키 값이 루트보다 작으면 왼쪽 자식을 기준으로 다시 탐색
- 키 값이 루트보다 크면 오른쪽 자식을 기준으로 다시 탐색
순환적인 탐색 함수
BinaryNode* searchRecur( BinaryNode *n, int key ) { //루트노드 n과 서브트리에서 키값이 key인 노드를 찾아서 반환하는 함수 if( n == NULL ) return NULL; if( key == n->getData() ) return n; else if (key < n->getData() ) return search( n->getLeft(), key ); else return search( n->getRight(), key ); }
반복적인 탐색 함수
BinaryNode* searchIter( BinaryNode *n, int key ) { //키값으로 노드를 탐색하는 함수로 일반 함수로 BinarySearchTree의 멤버 함수로 구현한다. while(n != NULL){ if( key == n->getData() ) return n; else if (key < n->getData() ) n = n->getLeft(); else n = n->getRight(); } return NULL; }
순환적인 탐색 함수
BinaryNode* BinaryNode::search( int key ) { //키값으로 노드를 탐색하는 함수로써 노드 클래스의 멤버로 구현된다. 일반 함수가 아니다. if( key == data ) return this; else if (key < data && left!=NULL) return left->search(key); else if (key > data && right!=NULL) return right->search(key); else return NULL; }
삽입연산
insert(n) : 이진 탐색 트리의 특성을 유지하면서 새로운 노드 n을 이진 탐색 트리에 삽입한다.
- 탐색연산을 먼저 수행한다.
- 같은 키 값을 가지는 노드가 없어야 한다.
- 탐색 실패의 경우 해당 위치에 삽입을 해준다.
void insertRecur( BinaryNode* r, BinaryNode* n ) { //서브트리의 루트 노드 r, 삽입하고자 하는 노드 n if( n->getData() == r->getData() ) return; else if( n->getData() < r->getData() ) { if( r->getLeft() == NULL ) r->setLeft(n); else insertRecur( r->getLeft(), n ); //순환호출 } else { if( r->getRight() == NULL ) r->setRight(n); else insertRecur( r->getRight(), n ); //순환호출 } }
삭제연산
remove(n) : 이진 탐색 트리의 특성을 유지하면서 노드 n을 트리에서 삭제한다.
case1
삭제하려는 노드가 단말 노드일 경우
알아야할 정보 => (삭제할 노드, 삭제할 노드의 부모 노드)
- 단말노드의 부모노드를 찾는다.
- 단말노드의 부모노드의 링크필드를 NULL로 만들어서 연결을 끊는다.
void remove (BinaryNode *parent, BinaryNode *node) { // case 1 if( node->isLeaf() ) { if( parent == NULL ) root = NULL; else { if( parent->getLeft() == node ) parent->setLeft(NULL); else parent->setRight(NULL); } }```
case2
삭제하려는 노드가 하나의 서브트리만 가지고 있는 경우
알아야 할 정보 => (삭제할 노드, 삭제할 노드의 부모노드, 삭제할 노드의 유일한 자식노드)
- 삭제되는 노드가 가지는 하나의 서브트리를 확인한다.
- 삭제할 노드를 삭제한다.
- 유일한 자식노드를 삭제한 노드의 부모노드와 연결시켜준다.
// case 2 else if( node->getLeft()== NULL|| node->getRight()==NULL ) { BinaryNode *child = (node->getLeft() != NULL ) ? node->getLeft(): node->getRight(); if( node == root ) root = child; else { if( parent->getLeft() == node ) parent->setLeft(child); else parent->setRight(child); } }
case3
삭제하려는 노드가 두개의 서브트리를 가지고 있는 경우
알아야 할 정보 => (삭제할 노드, 삭제할 노드의 부모노드, 후계노드, 후계노드의 부모노드)
- 삭제할 노드을 삭제하고 해당 위치에 후계노드를 이동시킨다.
- 후계노드 : 왼쪽 서브트리에서 가장 오른쪽에 있는 노드 or 오른쪽 서브트리에서 가장 왼쪽에 있는 노드
- 이진 탐색 트리를 중위 순회했을 때, 각각 삭제할 노드의 바로 앞과 뒤에 방문되는 노드이다.
// case 3 else { BinaryNode* succp = node; BinaryNode* succ = node->getRight(); while (succ->getLeft() != NULL) { succp = succ; succ = succ->getLeft(); } if( succp->getLeft() == succ ) succp->setLeft(succ->getRight()); else succp->setRight(succ->getRight()); node->setData(succ->getData()); node = succ; } delete node; }
Big-O
알고리즘의 복잡도를 판단하는 척도는 공간복잡도와 시간복잡도로 이루어져 있다. Big-O표기법은 시간복잡도를 다룬다. 시간복잡도는 알고리즘 내의 연산 횟수와 관련이 있다.
- 시간 복잡도 : 알고리즘의 시간 효율성
- 공간 복잡도 : 알고리즘의 공간(메모리) 효율성
Big-O표기법
알고리즘이 해당 차수이거나 그보다 낮은 차수의 시간복잡도를 나타내는 표기법이다.
- 상수항 무시 : O(2N) => O(N)
- 영향력 없는 항 무시 : O(N^2 + 2N + 1) => O(N^2)
ex) f(n) = n^2 + n +3 => T(n) = n^2 => O(n^2)
알고리즘 성능비교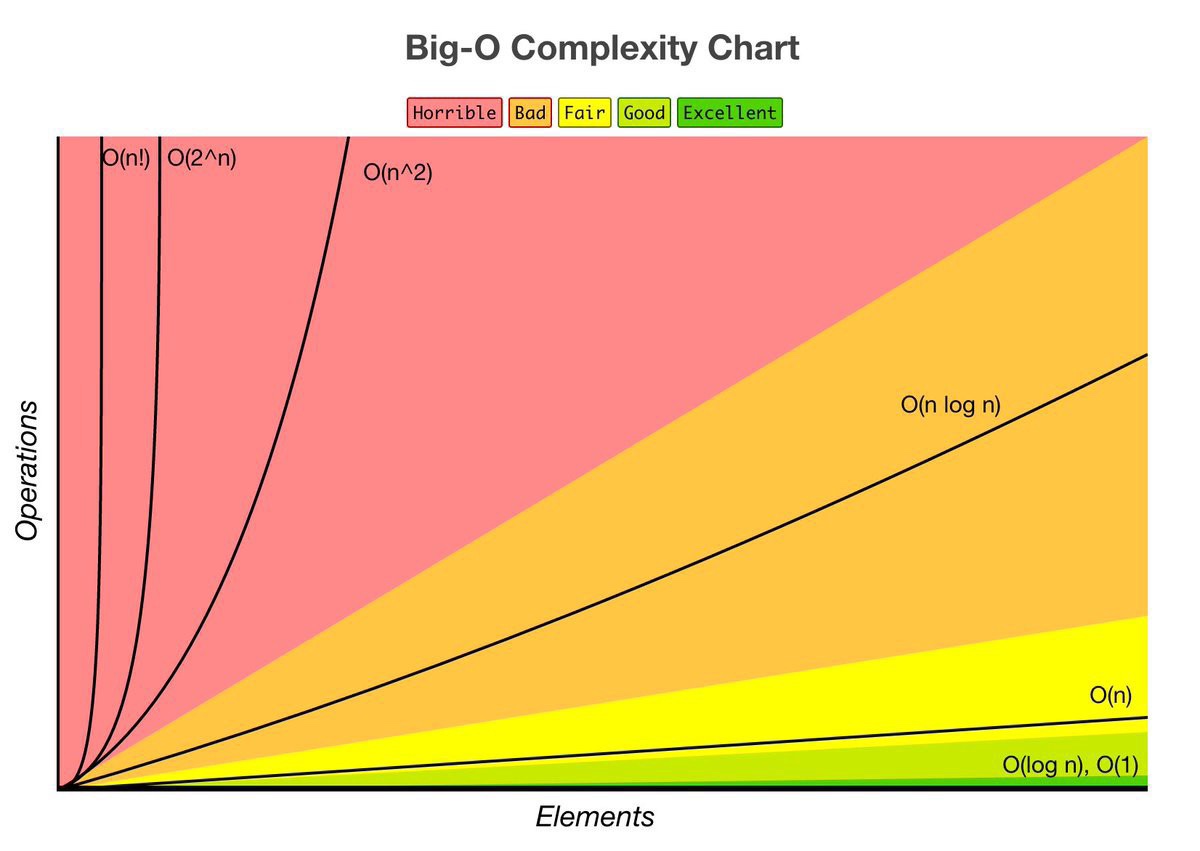
-
O(1) : 입력값에 상관없이 일정한 실행시간을 가지는 알고리즘이다. 하지만 상수값이 상상 이상으로 클 경우 사실상 일정한 시간의 의미가 없다.
-
O(log n) : 로그는 매우 큰 입력값에서도 크게 영향을 받지 않아 매우 견고한 알고리즘으로 이진 탐색의 경우가 이에 해당한다. input size의 값이 큰 경우에 사용한다.
-
O(n) : 알고리즘을 수행하는데 걸리는 시간은 입력값에 비례한다. 이러한 알고리즘을 선형 시간 알고리즘이라 부른다. element의 값을 하나하나 다 보는 경우에 사용한다.
-
O (n log n) : 병합 정렬등의 대부분 효율이 좋은 알고리즘이 이에 해당 한다. 아무리 좋은 알고리즘이라 할지라도 n log n 보다 빠를 수 없다. 입력값이 최선일 경우, 비교를 건너 뛰어 O(n)이 될 수 있다.
-
O(n^2) : 버블 정렬 알고리즘이 이에 해당 한다.
-
O(2^n) : 피보나치의 수를 재귀로 계산하는 알고리즘이 이에 해당 한다. n^2와 혼동되는 경우가 있는데 2^n이 훨씬 더 크다.
-
O(n!) : 가장 느린 알고리즘으로 입력값이 조금만 커져도 계산이 어렵다.
문제
LeetCode 98
문제설명
- 이진 트리의 루트가 주어지면 유효한 이진 검색 트리(BST)인지 확인한다.
- 노드의 왼쪽 하위 트리에는 노드 키보다 작은 키가 있는 노드만 포함된다.
- 노드의 오른쪽 하위 트리에는 노드 키보다 큰 키가 있는 노드만 포함된다.
- 왼쪽 및 오른쪽 하위 트리도 모두 이진 검색 트리여야 한다.
문제풀이
해당 트리가 이진 탐색 트리인지 확인하는 문제이다.
두 번째 예제에서 노드의 오른쪽 하위 트리에는 노드 키보다 큰 키가 있는 노드만 포함한다는 조건을 만족하지 않는다.
그러므로 부모 노드의 오른쪽 자식이면 부모 노드보다 커야 하고 부모 노드보다 작은 노드가 없는지 확인해야 한다.class Solution { public: // 재귀적으로 반복하기 위한 매개변수 // 현재 노드, 노드가 가져야하는 최소값, 노드가 가져야하는 최대값 bool isValid(TreeNode* root, TreeNode* low, TreeNode* high) { if(!root) return true; if(low && root->val <= low->val) return false; if(high && root->val >= high->val) return false; return isValid(root->right, root, high) && isValid(root->left, low, root); } bool isValidBST(TreeNode* root) { return isValid(root, nullptr, nullptr); } };<다른 코드>
중위탐색을 이용한 이진 트리 탐색
이진 탐색 트리에서 중위 탐색을 하게 되면 탐색한 노드들의 값들이 오름차순이 된다는 특징을 이용한다. 최근에 탐색한 값보다 값이 큰 경우에 이진 탐색 트리에 해당된다.class Solution { func isValidBST(_ root: TreeNode?) -> Bool { var isValid = true var ans = Int.min func find(_ node: TreeNode?) { if node == nil { return } find(node?.left) if ans < node!.val { ans = node!.val } else { isValid = false return } find(node?.right) } find(root) return isValid } }https://m42-orion.tistory.com/38
https://vapor3965.tistory.com/76?category=975115
LeetCode 99
문제설명
- BST(Binary Search Tree)의 루트가 주어졌는데, 여기서 트리의 정확히 두 노드의 값이 실수로 스왑되었다. 구조를 변경하지 않고 트리를 복구한다.
문제풀이
중위탐색을 이용하여 이진 탐색 트리를 오름차순으로 정리한해 나열한 뒤에 수정이 필요한 부분을 찾아 구조를 유지하면서 해당 두 값을 스왑해준다.
class Solution { private: TreeNode *first; TreeNode *second; TreeNode *pre; void inorder(TreeNode *root){ if(root==nullptr) return; inorder(root->left); if(first==nullptr && (pre==nullptr || pre->val >= root->val)){ first = pre; } if(first!=nullptr && pre->val >= root->val){ second = root; } pre = root; inorder(root->right); } public: void recoverTree(TreeNode* root) { if(root==nullptr) return; first = nullptr; second = nullptr; pre = nullptr; inorder(root); int temp = first->val; first->val = second->val; second->val = temp; } };
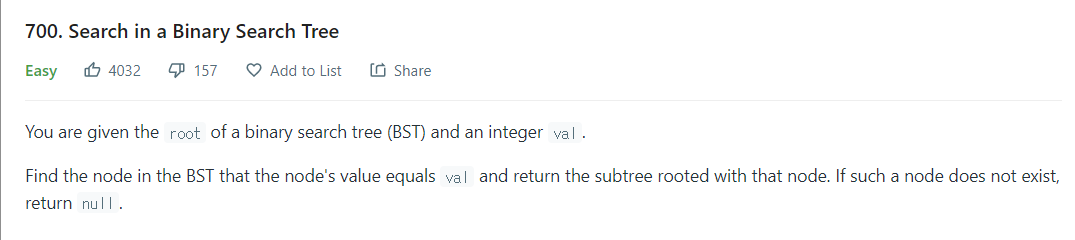
LeetCode 700
문제설명
이진 탐색 트리(BST)의 루트와 정수 val이 제공된다.
BST에서 노드의 값이 val과 같은 노드를 찾고 해당 노드를 기반으로 하는 하위 트리를 반환한다. 그러한 노드가 존재하지 않으면 null을 반환한다.문제풀이
루트 노드를 기준으로 정렬되었을 경우
public TreeNode searchBST(TreeNode root, int val) { if(root == null) return null; if(root.val == val) return root; // 조건 ? 참일 경우 실행 : 거짓일 경우 실행 return root.val > val? searchBST(root.left,val) : searchBST(root.right,val); }루트 노드를 기준으로 정렬되지 않았을 경우
깊이 우선 탐색을 이용하여 재귀호출을 통해 찾고자 하는 노드를 찾아간다.class Solution { public: TreeNode* searchBST(TreeNode* root, int val) { if(root == nullptr) return nullptr; if(root->val == val) return root; TreeNode *left = searchBST(root->left, val); if(left != nullptr){ return left; } else{ return searchBST(root->right, val); } } };너비 우선탐색을 이용한 경우
반복적으로 큐에 노드를 넣고 모든 노드를 검사해가면서 찾고자하는 값을 찾는다.public TreeNode searchBST4(TreeNode root, int val) { if(root == null) return null; Queue<TreeNode> q = new LinkedList<>(); q.offer(root); while(!q.isEmpty()){ TreeNode cur = q.poll(); if(cur.val == val) return cur; if(cur.left != null) q.offer(cur.left); if(cur.right != null) q.offer(cur.right); } return null; }
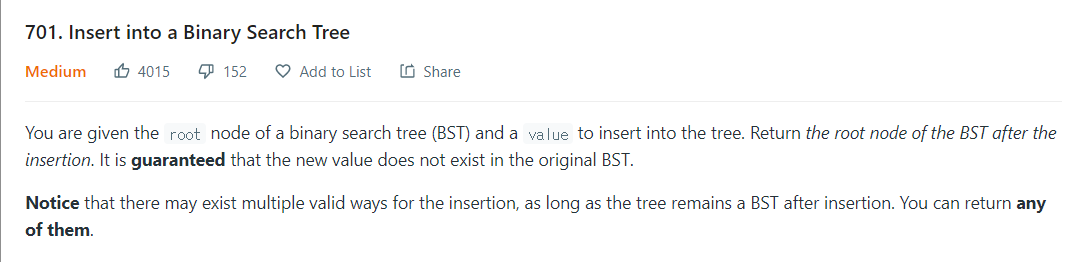
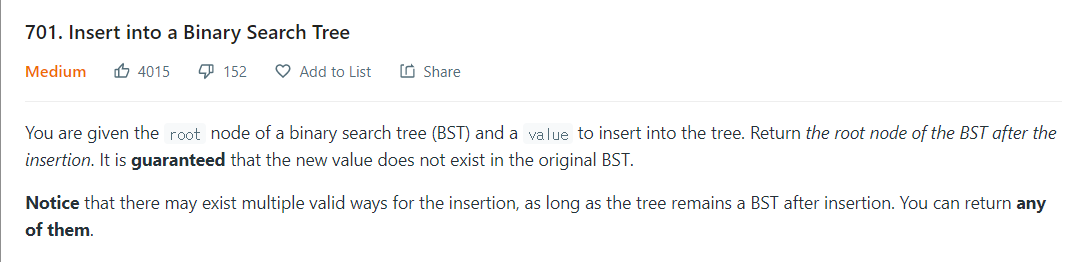
LeetCode 701
문제설명
- 이진 검색 트리(BST)의 루트 노드와 트리에 삽입할 값이 제공됩니다. 삽입 후 BST의 루트 노드를 반환합니다. 새로운 값이 원래 BST에 존재하지 않음을 보장합니다.
- 삽입 후 트리가 BST를 유지하는 한 삽입을 위한 여러 유효한 방법이 있을 수 있습니다. 당신은 그들 중 하나를 반환할 수 있습니다.
문제풀이
재귀호출을 이용하여 해당 노드보다 클 경우 오른쪽 노드에 재귀호출, 작을 경우 왼쪽에 재귀호출을 한다.
class Solution { public: TreeNode* insertIntoBST(TreeNode* root, int val) { if(root==nullptr) return new TreeNode(val); if(root->val > val){ root->left = insertIntoBST(root->left,val); }else{ root->right = insertIntoBST(root->right,val); } return root; } };추가
재귀호출을 사용하지 않고 반복하는 경우class Solution { public: TreeNode* insertIntoBST(TreeNode* root, int val) { if(root==nullptr) return new TreeNode(val); TreeNode* cur = root; while(cur != nullptr){ if(cur->val > val){ if(cur->left == nullptr){ cur->left = new TreeNode(val); break; }else{ cur = cur->left; } }else{ if(cur->right == nullptr){ cur->right = new TreeNode(val); break; }else{ cur = cur->right; } } } return root; } };