0. 문제
문제 설명
OO 연구소는 한 번에 K 칸을 앞으로 점프하거나, (현재까지 온 거리) x 2 에 해당하는 위치로 순간이동을 할 수 있는 특수한 기능을 가진 아이언 슈트를 개발하여 판매하고 있습니다. 이 아이언 슈트는 건전지로 작동되는데, 순간이동을 하면 건전지 사용량이 줄지 않지만, 앞으로 K 칸을 점프하면 K 만큼의 건전지 사용량이 듭니다. 그러므로 아이언 슈트를 착용하고 이동할 때는 순간 이동을 하는 것이 더 효율적입니다. 아이언 슈트 구매자는 아이언 슈트를 착용하고 거리가 N 만큼 떨어져 있는 장소로 가려고 합니다. 단, 건전지 사용량을 줄이기 위해 점프로 이동하는 것은 최소로 하려고 합니다. 아이언 슈트 구매자가 이동하려는 거리 N이 주어졌을 때, 사용해야 하는 건전지 사용량의 최솟값을 return하는 solution 함수를 만들어 주세요.
예를 들어 거리가 5만큼 떨어져 있는 장소로 가려고 합니다.
아이언 슈트를 입고 거리가 5만큼 떨어져 있는 장소로 갈 수 있는 경우의 수는 여러 가지입니다.
- 제한 사항
숫자 N: 1 이상 10억 이하의 자연수
숫자 K: 1 이상의 자연수입출력 예
N = 5, return = 2
N = 6, return = 2
N = 5000, return 5
1. 나의 풀이
- K칸 앞으로 점프(이 경우 K만큼 건전지 사용)
- 현재 위치에서 2배의 위치로 순간이동(이 경우 건전지 사용X)
- n이 홀수라면, 순간이동으로 해당 위치에 도달할 수 없으므로 1칸 점프
- n이 짝수라면 순간이동을 사용하여 현재 위치의 절반의 거리로 이동 가능
def solution(n):
ans = 0
while n != 0:
if(n % 2 != 0):
n -= 1
ans += 1
n /= 2
return ans시간 복잡도가 O(log n)
로그 시간복잡도: 입력 데이터의 크기가 두배로 늘어날 때마다, 연산 횟수는 1회씩만 증가
이진 검색, 이진 트리연산, 분할 정복 알고리즘 등에서 찾아볼 수 있음
- n 이 증가함에 따라 반복에 횟수가 증가, 오버헤드 가능성 높음
2. 더 간결했던 다른사람풀이
def solution(n):
ans = 0
return bin(n).count('1')- 2진수로 변환하여 1의 개수를 세는 것
3. 속도비교
1) 반복문(n = 1 ~ 5000)
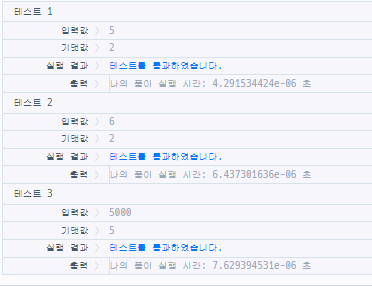
2) 2진수 변환(n = 1 ~ 5000)

3) 반복문이 빠른 것인가?
분명 결과적으론 5000까지에 숫자에서는 몇배 더 빨라보인다. 하지만 숫자가 커진다면 어떨까?
-
n = 90000486
-
반복문

-
2진수변환

-
숫자가 커질수록 2진수 변환이 빛을 발한다.