📘 참고서적
-
딥러닝을 위한 수학 - 신경망 수학기초부터 역전파와 경사하강법까지
-
혼자 공부하는 머신러닝 + 딥러닝
🛠️ 확률
<중점적으로 알아가고자 했던 용어>
표본공간, 사건, 이산, 연속, 조건부 확률, 역전파
- 표본공간
: 가능한 모든 사건의 집합 - 사건
: 표본공간 중에서 '특정'한 event - 이산 / 연속
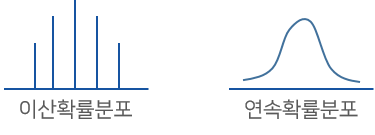
이산의 개념이 항상 헷갈렸는데 이번 기회에 머리에 완전히 각인 시켜둘 예정이다 👀
- 이산(離散) : 離(떠나다 리) 散(흩어지다 산) 한자 뜻에서 볼 수 있듯이 떨어져 있고, 흩어져 있다는 의미를 가지고 있다. 그래서 연속적이지 않다는 의미도 내포하고 있는 것이다!
- 연속 : 연속의 의미를 그동안 상당히 단순히 알고 있었는데, 아래에서도 살짝 언급할 거지만 베이즈 정리에 대해서 공부를 하다보면 연속에 대한 내용도 굉장히 복잡하다는 걸 알 수 있다. 여기서 간단하게만 적자면, 연속적이라는 것은 불확실하다는 의미와도 일맥상통한다.
(나는 최근 딥러닝 공부를 하다가 대가리가 터지는 현상을 겪고 있다. 정리하는 지금도 머리에서 열이 난다 ^^ 내 머리가 딥러닝 중)
-
조건부 확률
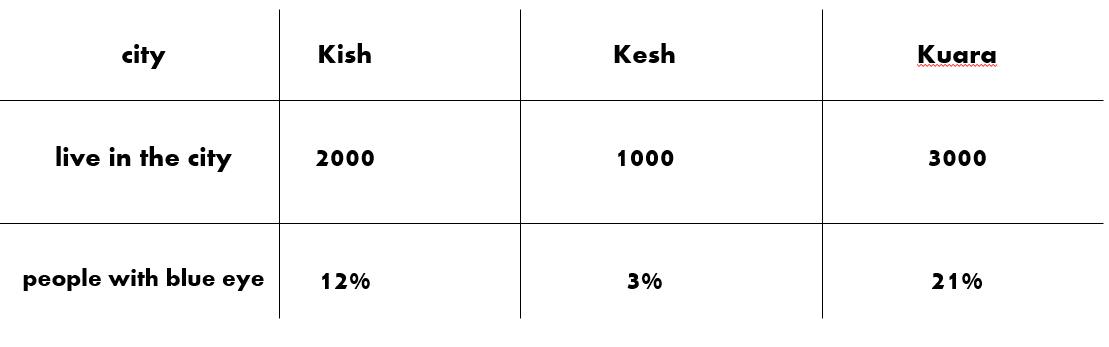
: P(BㅣA) 사건 A가 일어났다는 전제 하에 사건 B가 일어난다. 즉, 사건 A가 일어나야만 B도 일어난다는 것이다. (물론 두 사건이 독립적일 때는 특수한 상황으로써 계산 방법도 달라진다.)책에 나와있는 예시가 매우 좋아서 이해를 위해 올려본다.
세 도시 👨👩👦 Kish, Kesh, Kuara가 있다. 해당 세 도시에는 각각 2000, 1000, 3000명이 거주하고 있다. 세 도시에는 파란 눈을 가진 사람의 비율이 각각 12, 3, 21%이다.
❓ 그렇다면 세 도시에서 한 사람을 무작위로 선택했을 때, 그 사람이 파란 눈일 확률은 몇 퍼센트일까?
P(파란 눈) 👁️🗨️ = P(파란 눈ㅣKish) + P(파란 눈ㅣKesh) + P(파란 눈ㅣKuara)
P(파란 눈) 👁️🗨️ = P(파란 눈ㅣKish) x P(Kish) + P(파란 눈ㅣKesh) x P(Kesh) + P(파란 눈ㅣKuara) x P(Kuara)
이는 0.12 x 1/3 + 0.03 x 1/6 + 0.21 x 1/2 로 계산이 가능하다.
항상 조건부 확률을 공부하다 보면 '베이즈 정리'가 나온다. '베이즈 정리'는 <감정분류를 위한 한국어 감정 자질 추출 기법과 감정 자질의 유용성 평가> 논문을 읽고 공부한 내용을 정리해서 올리도록 하겠다.
-
역전파 (난 자꾸 고전파가 생각나서 미치겠다)
페이커짱우리미드짱해당 내용은 내가 아직 책 내용을 완전히 공부한 게 아니라 입문이라 보는 게 맞는 거 같다.
역전파를 알기 전에, 이 말에 대해서 알아가야 할 거 같다.
신경망의 훈련에는 손실함수가 관여한다.
이 때 손실함수는 뭘까? 손실함수는 지도학습을 하는 중, 해당 알고리즘이 얼마나 잘못 예측하는지를 체크하는 함수이다. (그래서 손실함수가 가장 크게 신경 쓰는 부분이 '최적화' 문제이다.)
💆♂️ 손실함수는 무조건 "연속"적이어야 한다. 그래야지 미분이 가능하기 때문이다.
손실함수의 종류는 크게 세 가지로 나눌 수 있다.
① 로지스틱 손실함수 (이진분류)
② 크로스엔트로피 손실함수 (다중분류)
③ 평균절댓값오차 MAE, 평균제곱오차 MSE (회귀)작년 게임인공지능 수업 때 분명 평균제곱오차에 대해 배웠던 기억이 있는데, 내가 제대로 기억을 하지 못하는 것 같기도 하고 평균절댓값오차에 대한 개념이 불투명해서 공부를 다시 했다.
해당 내용에 대해 잘 정리해둔 블로그가 있어 첨부한다. (https://heytech.tistory.com/379)
그렇다면 다시 본론으로 돌아와 과연 역전파는 뭘까?
손실함수는 L(𝜃)로 표기한다. 여기서 세타는 신경망의 모든 가중치와 치우침 값으로 이루어진 벡터인데, 손실함수는 이 세타에 대한 손실함수 L의 값이 최소가 되는 매개변수 값(손실함수의 능력치를 결정해주는, 쉽게 말하면 '스탯'들이다.)들의 집합을 찾는 것이다.
이 과정에서 L(𝜃)의 기울기가 쓰인다. 이 기울기값은 𝜕L/𝜕w 이다.
자, 여기서 결론이 나왔다! ("Learning Representations by Back-propagating Errors"라는 역전파를 세상에 처음 알린 논문이 있다고 한다! 나중에 시간이 되면 해당 논문을 정리한 글도 올리도록 하겠다.)
역전파는 기울기값(𝜕L/𝜕w) 을 구하는 것!
🧙 그동안 공부한 내용들을 한 번에 다 올리기는 뭣해서 가장 최근에 한 공부를 위주로 차근차근 올려봐야겠다. 차근차근 지금부터 해나가봐야겠다!