왜냐하면 역전파도 개짱이고 고전파도 개짱이기 때문이다
ㄴ 잡소리 죄송합니다
📘 참고 서적
- 딥러닝을 위한 수학 - 신경망 수학 기초부터 역전파와 경사하강법까지
- 딥러닝을 이용한 자연어 처리 입문 (https://wikidocs.net/37406)
역전파에 대한 고찰
아무리 공부를 해도 나는 도무지 역전파가 뭐하는 놈인지에 대해 정말 도저히 알 수가 없었다. 변명 아닌 변명을 하자면, 우선 내가 좋아하는 선수 중에 한 명의 닉네임과 너무 겹쳐서 집중이 안 됐다는 거고 두 번째로는 미분에 대한 총체적인 이해가 부족했기 때문이다.
혹시나 역전파에 대해 이해가 잘 안 된다면, 꼭 '미분의 연쇄 법칙(chain rule)', '편미분'에 대해 알아가보는 게 좋다 🤓
아마 chain rule에 대해서 알아가다 보면, 빠지지 않고 등장하는 게 편미분이니 굳이 편미분에 대해 더 검색을 하거나 그럴 필요는 없을 거다.
먼저, 역전파에 대해 알아가기 전 나름대로 정리가 필요했던 용어들을 정리해 보았다.
① 입력층, 은닉층, 출력층
② 시그모이드 함수
③ 미분 연쇄 법칙
④ 편미분
- 입력층, 은닉층, 출력층 👊
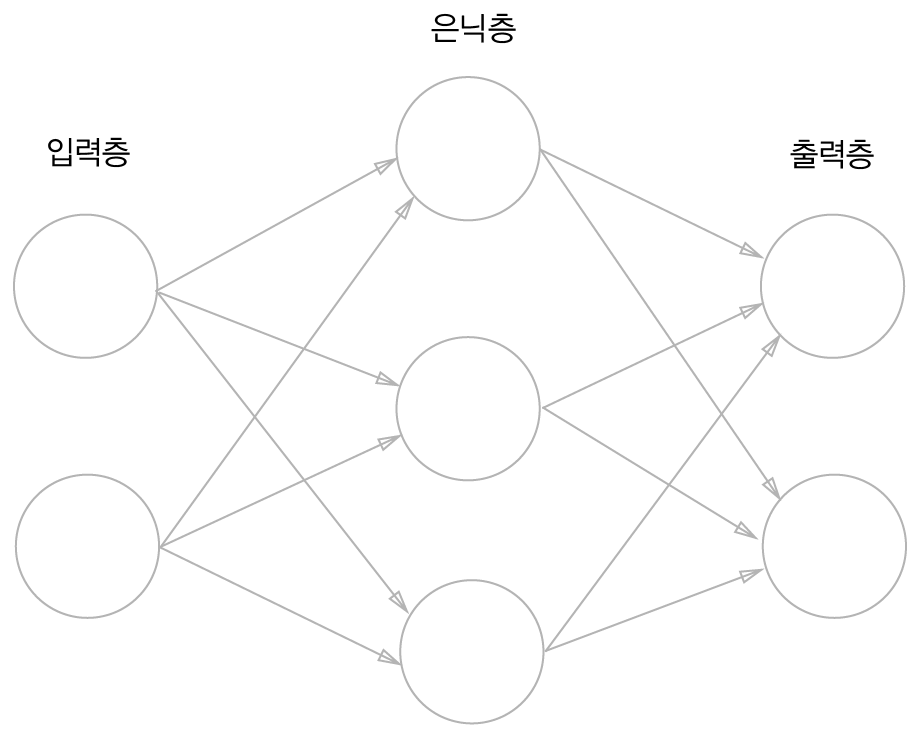
입력층 : 입력 벡터가 자리 잡는 층
은닉층 : 입력층과 출력층 사이에 위치하는 모든 층 (햄버거 패티 역할)
출력층 : 최종 출력값이 자리 잡는 층
- 시그모이드(Sigmoid) 함수 🎩
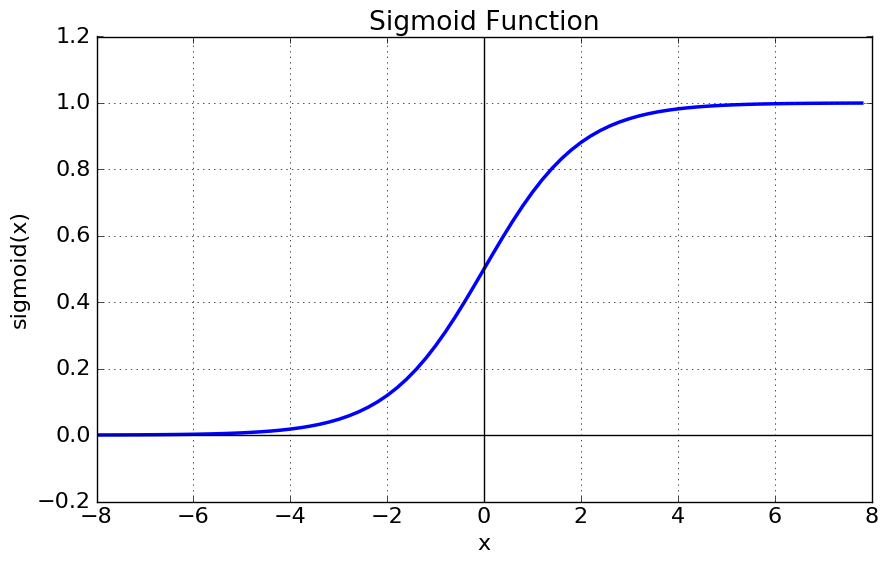
우리가 흔히 말하는 'S자형 함수'가 바로 시그모이드 함수이다. 해당 함수는 신경망에서 자주 쓰이는 활성화 함수 중 하나이다. 주로 로지스틱 손실함수의 레이어로써 자주 쓰인다. 시그모이드 함수에 대해 잘 설명해둔 사이트를 첨부하도록 하겠다. (https://icim.nims.re.kr/post/easyMath/64)
- 미분 연쇄 법칙(chain rule) 🦈

위의 사진은 내가 고등학교 시절 때 코 찔찔 흘리면서 배웠던 합성함수 미분법이다. 그 때는 그냥 그렇구나🤮 알빠?를 시전하였지만 이제는 다시 보인다. 해당 미분법은 미분 연쇄법칙이나 마찬가지였던 거다.
'chain'이라는 말에서 알 수 있듯이, 미분 연쇄 법칙은 합성함수를 각 함수의 미분의 곱으로 표현하는 거다. 계속 이어진다는 의미인 것이다. (이 말이 잘 이해가 되지 않는다면 이제부터 아래에 역전파를 직접 계산하면서 설명하도록 하겠다.)
- 편미분 🐻❄️
 편미분은 조금 쉽게 말하자면 미분할 '편'을 만드는 것과 같다. 그러니까, 하나의 변수에 대해서만 미분을 하고 나머지 변수들은 상수 취급하는 것이다. 해당 예제를 보면 아마 이해가 잘 될 것이다.
편미분은 조금 쉽게 말하자면 미분할 '편'을 만드는 것과 같다. 그러니까, 하나의 변수에 대해서만 미분을 하고 나머지 변수들은 상수 취급하는 것이다. 해당 예제를 보면 아마 이해가 잘 될 것이다.
그렇다면 대체 왜? 어째서? 역전파를 사용하는 것일까.
사실 인공지능 신경망 학습에 있어서 가장 중요한 것은 '최적화', 즉 오차를 줄여나가는 것이다. 이를 위해 경사하강법을 이용해 오차가 최소인 기울기 값을 찾아야 한다. 하지만 이 과정에서 합성함수의 차수는 계속해서 커지기 마련이고, 그 과정은 매우 복잡해질 것이다. 그렇기 때문에 아까 위에서 말한 미분의 연쇄법칙을 이용해 그 이전 값을 연쇄적으로 구하는 과정이 필요한 것이다. 이 과정이 결국은 '역전파'인 것이다.
'왜? 어째서? 역전파를 사용하는 것일까'에 대한 결론
신경망 학습에 있어 오차를 최소로 하기 위한 '기울기 값'을 구하기 위해서는 합성함수의 기울기가 필요하다. 이를 구하기 위해서는 미분의 연쇄법칙이 필요하다.
이 과정이 결국 '역전파'인 것이다.
예시를 통한 역전파 이해
사실 나는 역전파를 완전히 이해하지는 못했다. 참고서적에 있는 예시들을 겨우 이해하고 직접 계산해 보았을 뿐이다.
해당 자료는 '딥러닝을 이용한 자연어 처리 입문 (https://wikidocs.net/37406)'에서 참고하였다. 나름 이해한 내용을 적어보도록 하겠다.
또한, 해당 자료를 이해하기 위해서 '딥러닝을 위한 수학 - 신경망 수학 기초부터 역전파와 경사하강법까지'를 활용하였다.
💍 예시
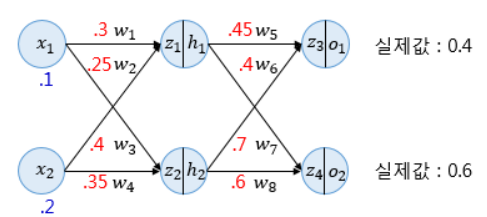
예시를 계산하기 전, 먼저 시그모이드 함수와 손실함수는 아래와 같다.
(위 - 시그모이드 함수 / 아래 - 손실함수)
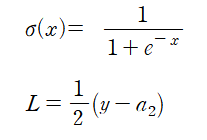
① 순전파 계산
이 때, 순전파란 그냥 단순히 왼쪽에서 오른쪽, 즉 순방향으로 계산하는 것을 말한다.

② 역전파 계산
역전파 계산은 순전파 계산과 달리 역방향으로 진행된다. 해당 예시에서는 총 2단계에 걸쳐서 진행되는데, 1단계의 방법과 2단계의 방법이 똑같아서 1단계 방법을 이해하고 정리한 것만 올린다.

휴 오늘도 정말 힘들었다 🐸 그나마 오늘은 TFT 8.5시즌이 나왔기 때문에 살아있는 게 아닐까 싶다 ^^ 그렇다면 내일도! 열공하는 걸로 하면서 이렇게 마무리~
