📘 참고서적
- 딥러닝을 위한 수학 - 신경망 수학기초부터 역전파와 경사하강법까지
오늘의 공부 순서는 다음과 같다 🤔
- 다양한 종류의 통계량 알아보기
- 데이터 집합을 요약 통계량으로 특징짓는 방법
- 분위수 소개
- 그래프를 통해 데이터 내용 파악
- 이상치와 결측자료에 대한 설명
- 나쁜 데이터 검출 및 누락된 데이터 처리 방법
- 변수들 사이의 상관관계 논의
- 통계적 가설 검정
와! 4일이나 걸렸다. 근데 다 이해 못함
다양한 종류의 통계량 알아보기
통계랑(Statistic)
어떠한 표본에서 계산한, 그리고 그 표본을 어떠한 방식으로 특징 짓는 수치
📁 데이터의 종류
데이터는 '척도(Scale)'로 구분된다. 이는 크게 질적 자료와 양적 자료, 두 가지로 나뉜다.
- 질적 자료(Quantitative) : 숫자로 표현할 수 없는 정보
- 명목형 자료
- 순서형 자료 - 양적 자료(Qualitative) : 숫자로 표현할 수 있는 정보
- 구간 자료
- 비율 자료
🏷️ 명목형 자료(Nominal Data)
범주형 자료(Categorical data)라고 불리기도 한다. 명목형 자료는 서로 다른 값들 사이에 순서 관계가 없는 데이터이다.
- 명목형 자료의 심층학습
신경망학습에서는 명목형 자료를 처리할 수 있도록 과정을 거쳐야 한다.
예를 들어 빨강, 파랑, 노랑은 명목형 자료로써 순서가 없다. 그러나 단순하게 이를 빨강 - 1 / 파랑 - 2 / 노랑 - 3 으로 변환을 하는 것은 바람직하지 않다. ('파란색이 빨간색에 비해 두 배 크다.'라고 이해할 수 있기 때문이다.) 그렇다면 무슨 방법을 써야할까?
바로 '원핫부호화(One-hot encoding)'이다.
👉 '빨간색 - 0 0 1 / 파란색 - 0 1 0 / 노란색 - 1 0 0'와 같이 표현하는 것이다.
🏷️ 순서형 자료(Ordinal Data)
순위 또는 순서가 있는 데이터이다. (단, 값들의 차이에 어떤 수학적 의미가 있는 것은 아님.)
🏷️ 구간 자료(Interval Data)
값들의 차이에 의미가 있는 데이터이다.

이렇게 설명이 가능하다고 하는데, 사실 이해가 잘 되지 않아서 예시를 더 찾아 보았다. 다양한 예시 중에서 빠지지 않고 늘 등장하는 것이 바로 '온도'였는데, 온도의 '0도'에서 '0'은 존재하지 않는 숫자가 아니다. 즉, 0도라고 해서 '온도가 없는' 것은 아닌 것과 같다. 그러나 80도와 40도 간의 온도 차이는 40도라고 표현할 수 있다. 그래서 처음 설명했던 값들의 차이에 의미가 있다는 것이다.
🏷️ 비율 자료(Ratio Data)
값들의 차이에 의미가 있을 뿐 아니라, 진정한 영점(Zero Point)가 존재하는 데이터로 구간 자료와 차이가 있다. 예시로 키가 0cm이면, 이는 높이가 아예 존재하지 않는 것이므로 비율 자료라고 할 수 있다.
🙋♂️ 여기서 잠깐!
온도는 항상 '구간 자료' 가 아닐 수도 있다?화씨나 섭씨 단위로 측정한 온도는 '구간 자료'이지만, 켈빈 단위의 절대 온도는 '비율 자료'이다. 왜냐하면, 0켈빈은 온도가 '아예 없다'는 것을 의미하기 때문이다.
데이터 집합을 요약 통계량으로 특징짓는 방법
요약 통계량(Summary statistic)
요약 통계량은, 데이터 집합을 더 잘 이해할 수 있도록 데이터 집합의 특징을 파악하는 방법이다.
종류는 다음과 같다.
- 평균
- 기하평균
- 조화평균 - 중앙값
- 평균편차
- 편향 표본분산
- 표본분산
- 표준오차
- 표준편차
- 분위수
차례대로 알아가겠다!
👨🦳 평균
우리가 흔히 알고 있는, 모든 수를 다 더 해서 수들의 개수로 나누는 것을 '산술평균(Arithmetic mean)', 정확히는 '비가중(unweighted)' 산술 평균이라고 부른다.
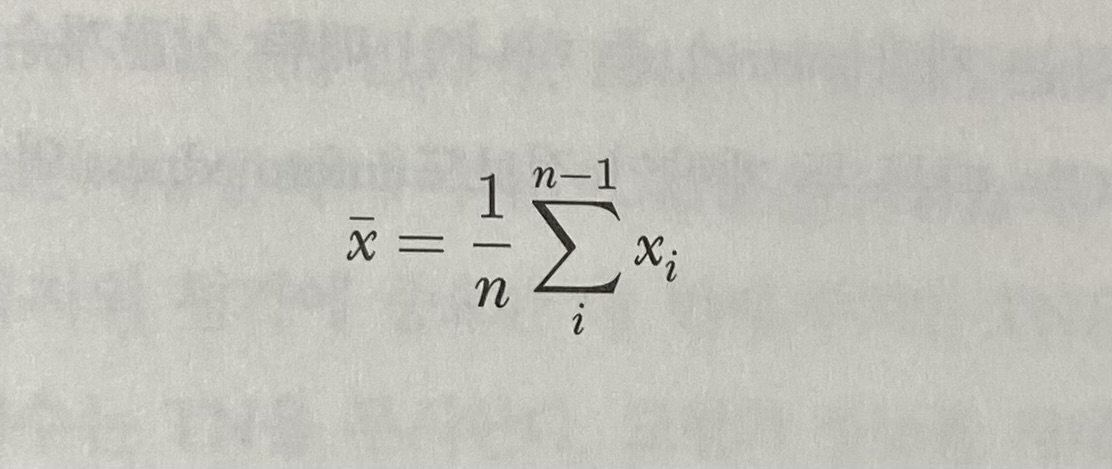
다음과 같은 식으로 표현할 수 있다.
이 때, '비가중'이라는 뜻은 데이터 집합의 요소들이 모두 고른 가중치, 즉 1/n의 가중치가 부여된다는 의미이다. 그렇다면, 가중(weighted) 산술평균도 존재하지 않을까? 가중 산술평균은 아래와 같이 나타낼 수 있다.
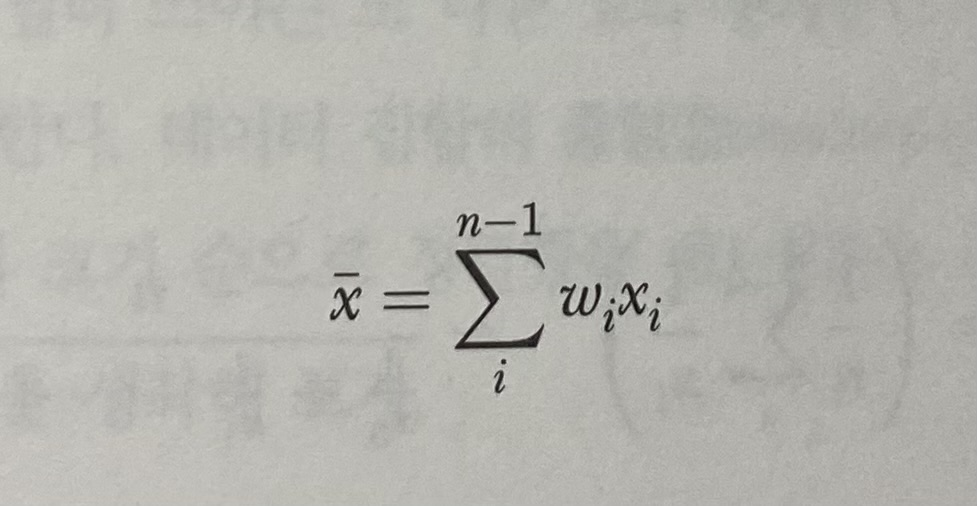
👧 기하평균(Geometric mean)
두 양수 a와 b의 기하평균은 두 양수의 곱의 제곱근이다. 이를 일반화하자면, 양수 n개의 기하 평균은 그 곱의 n제곱근이다.
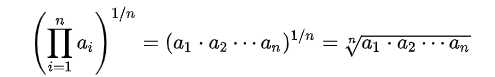
위의 식처럼 표현할 수 있다.
기하평균이 필요한 이유는 뭘까? 기하평균은 '비율 증가'에 대한 평균을 나타내는 값이기 때문이다.
예를 들어, 4cm 길이의 자를 2배 늘리면 8cm이고, 이를 또 4배하면 32cm이다. 이 때, 우리가 단순하게 계산하는 산술평균처럼 평균적으로 (2+4)/2 = 3배 늘었다고 설명할 수 있을까? 이는 비율의 평균을 다루는 문제이기 때문에 틀린 답이다. 그래서 루트를 씌우는 것이다!
👧 조화평균(Harmonic mean)
두 수 a와 b의 조화평균은 그 역수들의 산술 평균의 역수이다.
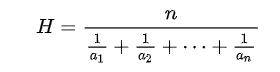
조화평균은 F1 Score에서 다시 등장한다. F1 Score는 recall과 precision의 조화 평균이다.
👨🦳 중앙값(Median)
중앙값은 말 그대로 딱 '중앙'에 있는 값이다.
X = {2, 3, 4, 5, 6} 과 같은 식이 있다면, 이 때 중앙값은 '4'이다. 그러나 X 집합이 다음과 같다면 어떻게 될까?
X = {2, 3, 4, 5, 6, 7} 과 같이 짝수 개라면 '완전한' 중앙값이 없다. 이 때는, 4와 5의 평균값을 사용해서 4.5가 위 X 집합의 중앙값이다.
🧠 평균과 중앙값의 차이는?
: 평균은 데이터 값들의 합을 반영하고, 중앙값은 데이터 집합의 요소들을 크기순으로 절반으로 나누는 지점이다.평균은 값들 크기 그 자체에 집중하고, 중앙값은 단순히 값들의 대소(순서)에 집중한다.
✍️ 편차와 분산을 쓰는 이유
👀 편차와 분산을 쓰는 이유는 뭘까?
: 데이터를 분석하다 보면, 데이터의 값들이 평균에서 얼마나 '떨어져 있는가?', 즉 '변동(Variaition)'에 대한 질문이 생긴다. 이를 파악하기 위해서 편차와 분산이 존재한다.
✨ 평균편차(Mean deviation)
평균편차는 각 값이 평균적으로 전체 평균과 얼마나 떨어져 있는지를 말해준다.
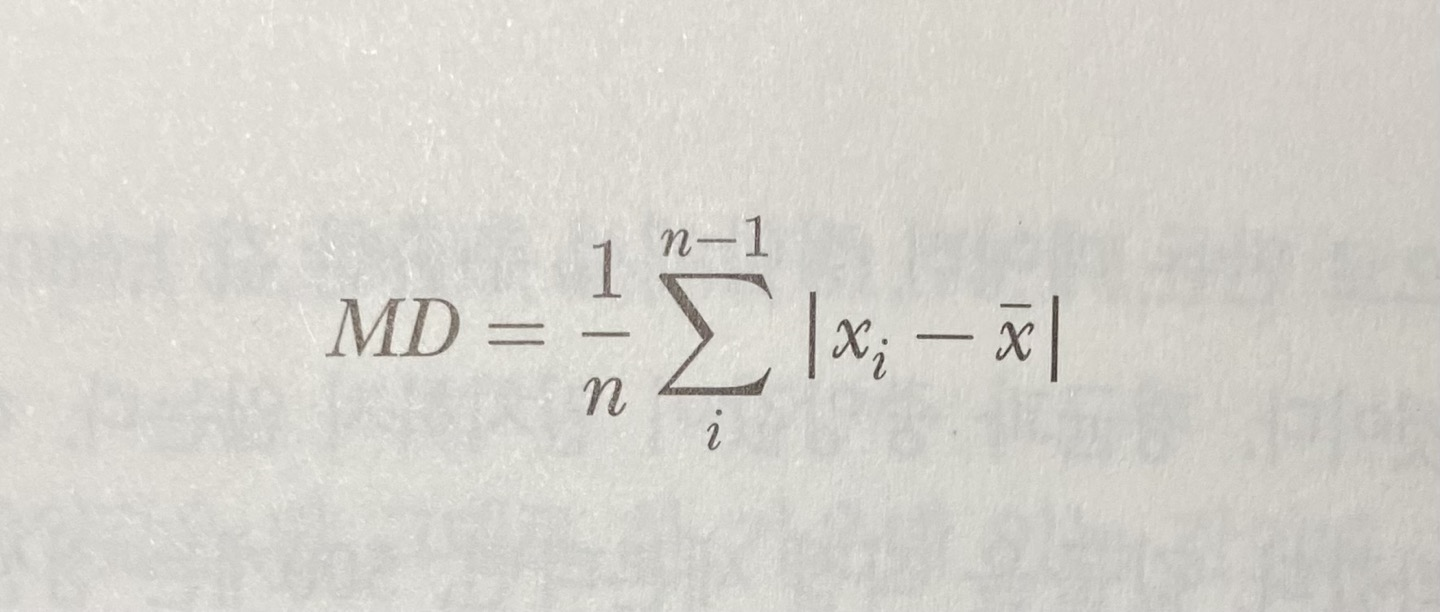
평균편차의 까다로운 점은 '절댓값'이다. 그래서 다음과 같이 차이의 제곱들의 평균, 즉 '편향 표본분산'이 자주 쓰인다.
✨ 편향 표본분산(Baised sample variance)
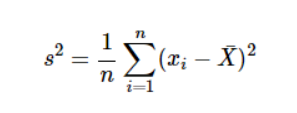
수식에서 볼 수 있듯이, 편향 표본분산은 데이터 집합의 각 값과 평균의 차이의 제곱들의 평균이다.
'편향'이라는 말의 뜻은, 어디론가 치우쳐 있다는 것과 같다.
편향, 분산에 대한 내용을 잘 다룬 블로그 링크를 첨부한다.
(https://opentutorials.org/module/3653/22071)
✨ 비편향 표본분산(Unbaised sample variance)
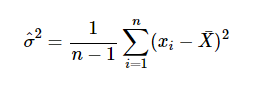
편향 표본분산을 보다가 보면, 가끔 위와 같은 식을 보게 된다. 편향 표본분산과 달리 비편향 표본분산은 n 대신 n-1을 사용한다. 이는 잔차(residual)과 연관이 있다.
🙋♀️ 잔차란?
표본(Sample)으로 추정한 회귀식의 값과 실제 관측값의 차이를 의미한다.
근데 찾아보니 오차와 다른 점이 도무지 뭔지 모르겠다는 생각이 들었다. 그도 그럴 것이, 오차의 정의는 모집단(Population)으로 추정한 회귀식의 값과 실제 관측값의 차이이다. 대체 모집단과 표본의 차이가 뭐지?
🙋♀️ 모집단과 표본의 차이는 뭐지?
간단하게 생각하자면, 모집단에서 특정하게 뽑은 것을 표본이라고 하는 것이다.
다시 본론으로 돌아와, n-1을 사용하는 이유는 정확하게 말하자면 잔차들의 자유도와 관련이 있다. 잔차들의 합은 0이다. 그렇기 때문에 데이터 집합의 값이 n개일 때, n-1개의 잔차를 알면 나머지 한 잔차는 간단하게 계산할 수 있다. 이는 잔차들의 자유도가 증가하는 것이다. 이렇게 되면 분산의 추정치가 덜 편향된다.
인데 ...

사실 나도 이 부분은 무슨 말인지 잘 모르겠다. 알게 되면 더 보충해서 적도록 ...
✨ 표준오차(Standard error)
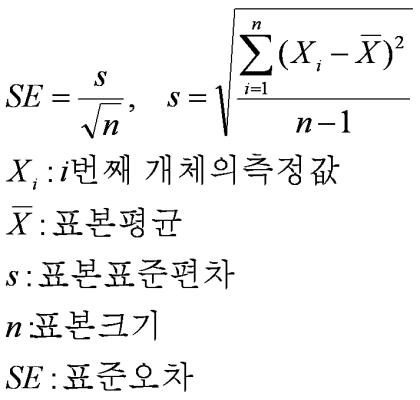
표준오차는 표본평균들의 집합의 표준편차이다.
✨ 표준오차 vs 표준편차
표준오차는 표본평균이 모집단 평균을 얼마나 잘 추정한 것인지 파악하는 데 유용하고, 표준편차는 평균을 중심으로 값들이 얼마나 흩어져 있는지 파악하는 데 유용하다.
해당 내용을 잘 정리해놓은 블로그, 유투브 링크를 첨부한다.
(https://blog.naver.com/istech7/50151940343)
(https://www.youtube.com/watch?v=TrIXkIHSqq4)
너무 어려워서 아직도 정확히 이해하진 못했다.
분위수 소개
🌟 분위수(Quantile)
분위수는 데이터 집합을 고정된 크기(값들의 개수)를 여러 그룹(분위)으로 나누는 값을 말한다. 그러니까, 중앙값은 데이터 집합을 같은 크기의 두 그룹으로 나누기 때문에 이분위수(2-quantile)이다.
흔히 데이터 집합을 사분위(quantile)라고 부르는 네 개의 그룹으로 나눈다. 1사분위(Q1)는 25% 값이 속하고, 2사분위(Q2)는 50% 값, 3사분위(Q3)는 75%, 그 나머지 25%의 값이 4사분위(Q4)에 속한다.
🌟 분위수에 대한 더 자세한 설명
이제 이 사진을 보고 더 자세하게 설명을 하도록 하겠다!
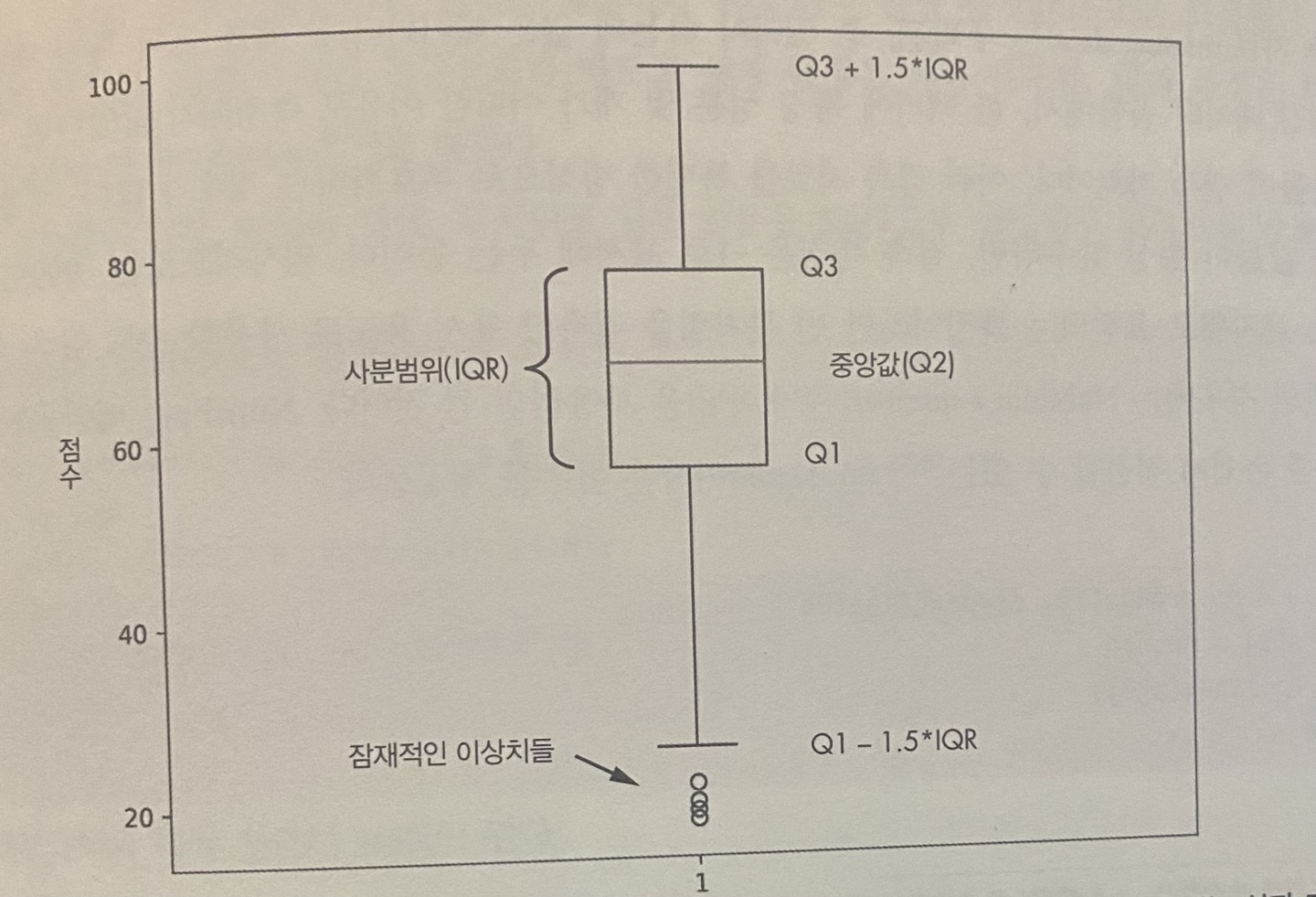
✨ 사분범위(IQR)
사분범위는 Q3와 Q1의 차이이다.
✨ 잠재적인 이상치(Possible outlier)
사분범위에서 빠져 나온 선들을 수염(Whisker)이라고 하는데, 이에서 빠져 나간 요소들이 있다. 이를 이상치라고 한다.
✨ 결측자료(Missing data)
🙋♀️ 여기서 잠깐! 이상치와 결측자료는 무슨 차이일까?
이상치는 일반적인 데이터 값에서 많이 벗어난 값이고, 결측자료는 아예 값 자체가 비어있는 것이다.
결측자료는 누락된, 즉 있어야 하는데 없는 데이터이다. 그래서 이를 사용하고 싶어서, 대부분 부호화하는 경우가 많다.
🥐 변수들 사이의 상관관계 논의
🥖 피어슨 상관계수(Pearson correlation coefficient)
숫자형 X 숫자형 변수 간의 모수적(정규분포)의 선형관계
두 특징 사이의 선형(두 특징의 상관관계가 얼마나 강한지) 상관관계의 세기를 뜻하는 [-1, +1] 구간의 수치이다.
- 한 특징이 일정한 양만큼 증가하였을 때, 다른 특징도 딱 그만큼 증가 => +1
- 한 특징이 일정한 양만큼 증가했을 때 다른 특징이 딱 그만큼 감소 => -1
- 두 특징이 연관되지 않음 => 0 (잠재적으로 독립)
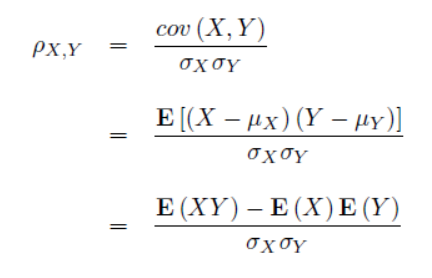
def pearson(x, y):
exy = (x*y).mean()
ex = x.mean()
ey = y.mean()
exx = (x*x).mean()
ex2 = x.mean()**2
eyy = (y*y).mean()
ey2 = y.mean()**2
return (exy - ex*ey)/(np.sqrt(exx-ex2)*np.sqrt(eyy-ey2))이와 같은 코드로도 구현이 가능하다.
🥖 스피어먼 상관계수(Spearman correlation coefficient)
숫자형 X 숫자형 변수 간의 비모수적 단조(일정 비율로 증가하지 않음)관계
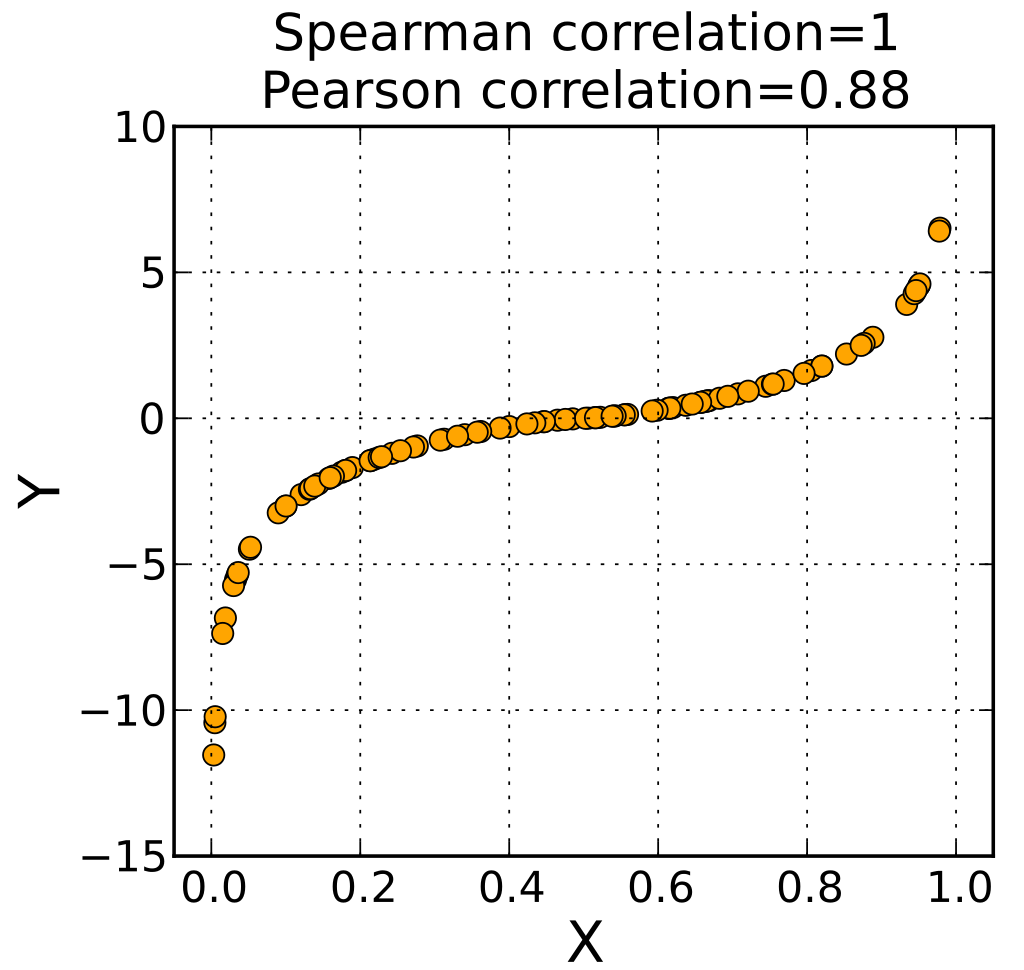
스파이먼 상관계수는 '순위(rank)가 매겨진' 변수 간의 피어슨 상관계수로 이해된다.
순위에 대한 내용을 더 이해하기 위해서 예시를 설명하겠다.
예를 들어 X가 다음과 같다.
X = [86, 62, 28, 43, 3, 92, 38, 87, 74, 11]
순위는 다음과 같다.
[7, 5, 2, 4, 0, 9, 3, 8, 6, 1]
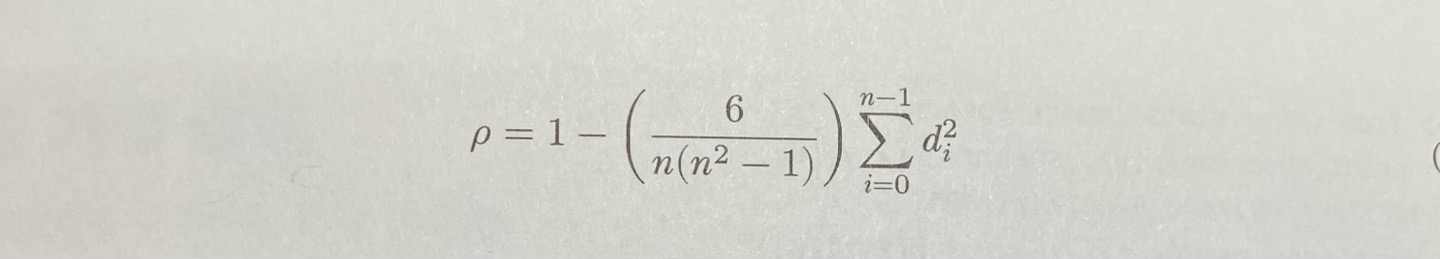
식은 위와 같이 표현할 수 있다. (단, X, Y에 중복된 순위들이 없어야 한다.) n은 값들의 계수이고, d는 rank(X) - rank(Y)이다. (이는 짝지은 X값과 Y값의 순위 차이이다.)
def spearman(x,y):
n = len(x)
t = x[np.argsort(x)]
rx = []
for i in range(n):
rx.appeend(np.where(x[i] == t)[0][0])
rx = np.array(rx, dtype = "float64")
t = y[np.argsort(y)]
ry = []
for i in range(n):
ry.append(np.where(y[i] == t)[0][0])
ry = np.array(ry, dtype = "float64")
d = rx - ry
return 1.0 - (6.0 / (n * (n*n-1))) * (d**2).sum()이와 같은 코드로 구현할 수 있다.
🥖 피어슨 상관계수와 스피어먼 상관계수의 근본적인 차이점
ramp = np.linspace(-20, 20, 1000)
sig = 1.0 / (1.0 + np.exp(-ramp))이와 같은 코드에서 ramp는 약 0.9인 반면, sig는 1.0이다. 피어슨 상관계수는 인수들 사이의 비선형 관계를 "암시"하기만 할 뿐이다. 그에 비해 스피어먼 상관계수는 인수들 사이의 비선형 관계를 반영하고 있다.
🎂 통계적 가설 검정
두 데이터 집합이 동일한 모분포에서 추출한 표본들인가?에 대한 질문의 답을 구하기 위해 통계적 가설 검정을 한다.
🍰 가설(Hypothesis)이 뭘까?
가설 검정에서는 두 종류의 가설을 사용한다.
- 귀무가설(Null hypothesis)
- 대안가설(Alternative hypothesis)
저번 학기 통계 수업 때 들었던, ...아주아주 무시했던 내용들이 떠올라 약간 ptsd가 온다.
귀무가설을 주로 쓰는데, 귀무가설(H_0으로 표기한다.)은 "두 데이터 집합이 사실은 같은 모집단에서 나왔을 것"이라는 뜻이다. (대안가설은 그와 반대이다.)
우리는 이 가설검정으로 두 데이터 집합이 같은 모집단에서 비롯됐는지에 대해서만 판단할 것이다. 이를 양면(two-sided) 검정이라고 한다.
뒤에 바로 설명할 t-검정을 적용할 때를 예로 들어보자.
🍿 계산한 검정통계랑(test stastic, 표본 데이터에서 계산되어 가설검정에 사용되는 랜덤 변수)들의 분포와 비교해서 계산한 t-값이 실제로 발생할 가능성이 어느 정도인지 파악한다. 검정 통계량이 그 분포의 특정 기준보다 큰지, 아니면 작은지 알고자 할 때 양면 검정을 사용한다.
위를 바탕으로 접근 방식을 아래와 같이 정리할 수 있다.
- 독립적인 두 데이터 집합을 비교하고자 한다.
- 두 데이터 집합의 표준편차가 같은지에 대해서는 아무런 가정도 하지 않는다.
- 귀무가설은 데이터 집합들의 모집단 평균들이 서로 같다는 것이다. 즉, H_0 : M_1 = M_2이다. 모집단 평균들을 알지 못하므로 표본 평균들과 표본 표준편차들을 사용해서 H_0을 승인할지, 기각할지 판정하는 데 필요한 증거를 얻는다.
- 가설 검정은 데이터가 독립 동일 분포(Independent and identically distribution, 서로 독립이고 각각 동일한 확률분포를 나타내는 다차원 확률변수)라고 가정한다.
🍰 t-검정(t-test)
t-검정은 t로 표기하는 검정 통계량에 의존한다. 이 통계량을 미리 만들어진 t-분포와 비교해서 p-값(H_0에 관한 결론을 내리는 데 사용하는 확률)을 구한다.
t-검정은 모수적(Parametric) 검정의 일종이다. 이 때, '모수적'이라는 말은 정규분포를 따른다는 말과도 같다.
t-검정도 종류가 많다. 책에서 설명하고 있는 것은 웰치의 t검정이다.
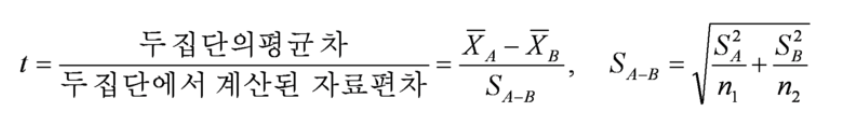
위의 식은 웰치의 t검정에서 t-점수를 계산하는 식이다.
t-점수들로 규정되는 t-분포의 곡선의 특정 구간(양의 t-점수 + 음의 t-점수로 결정됨)에서 곡선 아래의 면적을 계산한 값이 p-값이다.
p-값이 의미하는 바는, if 귀무가설이 참이라면 두 평균이 다를 확률이다.
p-값 다음으로 많이 나오는 단어가 신뢰구간(Confidence Interval, CI)이다. 이는 자유도와 관련이 있다. 신뢰구간은 우리가 비교하는 두 데이터 집합들의 반복된 표본들의 평균 차이들이 일정한 비율로 속하게 되는 진 모평균 차이들의 구간이다.
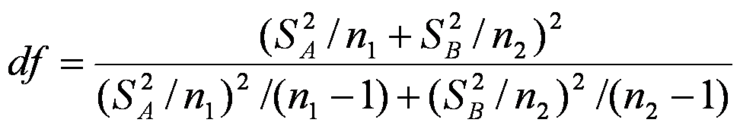
위의 식은 자유도를 계산하는 식이다. 자유도를 먼저 보여준 이유는 이를 활용해서 신뢰구간을 계산하기 때문이다.
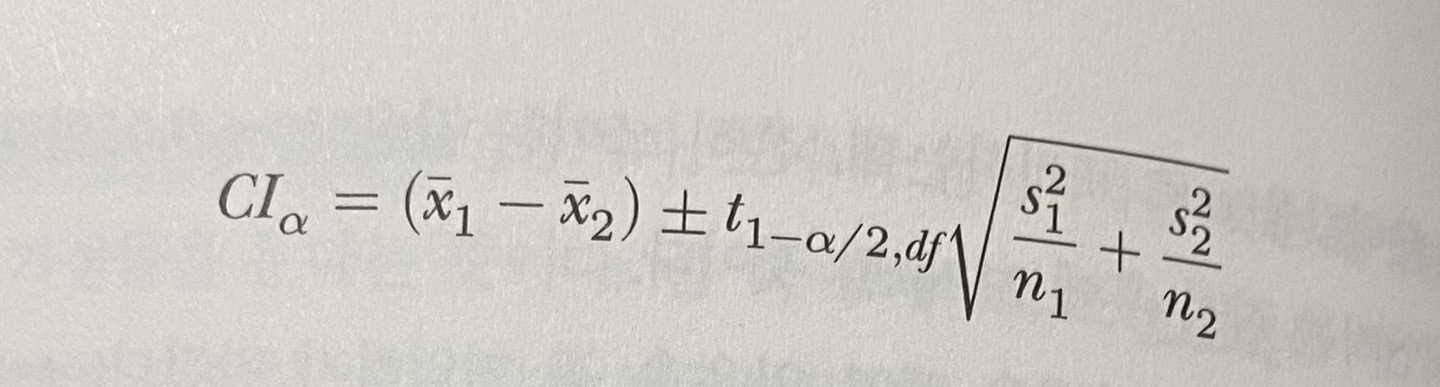
이해가 잘 안 되는 부분은 이 블로그를 참고했다.
(https://angeloyeo.github.io/2021/01/05/confidence_interval.html)
(https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=istech7&logNo=50151104309)
🍰 맨-휘트니 U 검정(Mann-Whitney U test)
맨-휘트니 U 검정은 두 데이터 집합이 같은 모분포에서 비롯한 것인지 판정할 때 도움이 되는 비모수적 검정이다.
맨-휘트니 U 검정의 검정 통계량 U이다.
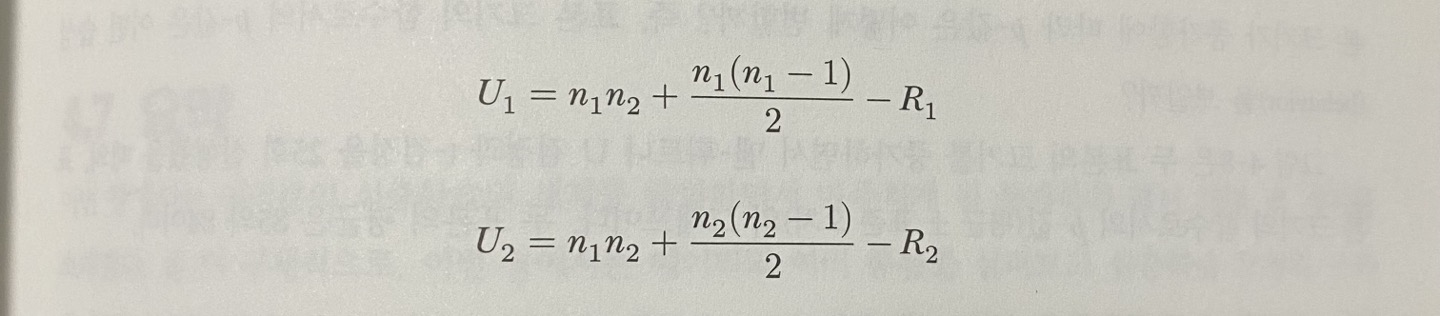
둘 중 더 작은 값이 맨-휘트니 U 검정의 검정 통계량 U이다.
맨-휘트니 U 검정을 위해서는 두 표본의 크기가 적어도 21이어야 한다. 그보다 작으면 결과를 신뢰하기 어렵다.

해당 장 공부를 끝내고 나서 (== 그냥 책을 읽고 모르는 부분에 동그라미 치면서 검색했다) 현재 내 상태다
나 인공지능 할 수 있는 거 맞아?

