Model-Contrastive Federated Learning

1. Introduction

FL이 왜 주목 받을까?

딥러닝 모델은 거대하고 잘 표현된 데이터셋에 영향을 많이 받습니다.

하지만 데이터는 보통 여러 곳에 퍼져있습니다.

프라이버시에 대한 고려, 데이터 보호 규제가 증가하면서 클라이언트들은 개인 데이터를 중앙 서버로 보낼 수 없습니다.

이런 도전 과제 속에서 FL이 등장했습니다.

FL은 다수의 클라이언트를 로컬 데이터 공유 없이 학습에 참여시킬 수 있기 때문입니다.

FedAvg란?

대표적인 FL 알고리즘이 FedAvg 입니다.

이름에서 알 수 있듯이, FedAvg는 서버로 전송된 로컬 모델 가중치를 평균 내어 글로벌 모델을 학습시킵니다.

원본 데이터를 교환하지 않고도 모델을 학습할 수 있는 거죠.

이런 장점으로 FL이 부상하기 시작했습니다.

FL의 주요 도전 과제

데이터 이질성 (data heterogeneity) 는 FL의 주요 도전 과제입니다.

실제 현실 세계에는 데이터가 불균등한 분포로 여러 클라이언트들에 퍼져있습니다.

이는 FL의 성능을 떨어뜨리는 원인이 되지요.

각 클라이언트가 본인의 로컬 모델을 업데이트하면, 로컬 목적은 글로벌 목적과 멀어집니다. 결국, 평균 낸 글로벌 모델이 글로벌 최적화로부터 멀어지는 거죠.

예를 들어, A는 고양이 사진만 많고, B는 강아지 사진만 많습니다. A는 고양이 사진 분류에 특화된 모델을 학습하게 되고, B는 강아지 사진에 특화된 모델을 학습하게 됩니다.

그러나 A, B의 로컬 모델을 서버로 보내서 평균 내어 집계하면 어떻게 될까요? 우리는 고양이도, 강아지도 잘 분류하는 글로벌 모델을 원하지만, 이도 저도 아닌 글로벌 모델이 만들어집니다. 고양이도 강아지도 잘 구분해내는 글로벌 모델이 아니라 둘 다 잘 구분 못하는 모델이 만들어지는 거죠.

heterogeneous 한 데이터로 인해 FL의 성능이 떨어진 것이죠. 이게 바로 FL의 주요 도전 과제입니다.

도전 과제를 해결하기 위한 시도들

FedProx는 $l_2$-norm distance를 적용해 로컬 업데이트를 제한합니다.

SCFFOLD는 variance reduction (분산 감소)을 통해 로컬 업데이트를 수정합니다.

하지만 이런 접근법들은 딥러닝 모델의 이미지 데이터셋에서 좋은 성능을 보여주진 못합니다. FedAvg만큼 나쁠 수 있습니다.

이 연구가 제안하는 방법은…

model-contrastive learning (MOON)을 제안합니다.

MOON은 (1) 현재 로컬 모델이 학습한 표현과 (2) 글로벌 모델이 학습한 표현의 일치가 최대화 되는 쪽으로 로컬 업데이트를 수정합니다.

MOON 실험 결과는

(1) CIFAR-10

(2) CIFAR-100

(3) Tiny-Imagenet

위 3가지 데이터셋에 대하여 다양한 이미지 분류를 수행했습니다.

FedAvg를 약간만 변경해서 대부분의 경우에서 최소 2% 정확도를 달성했습니다.

2. Background and Related work

2.1. Federated learning

• FedAvg

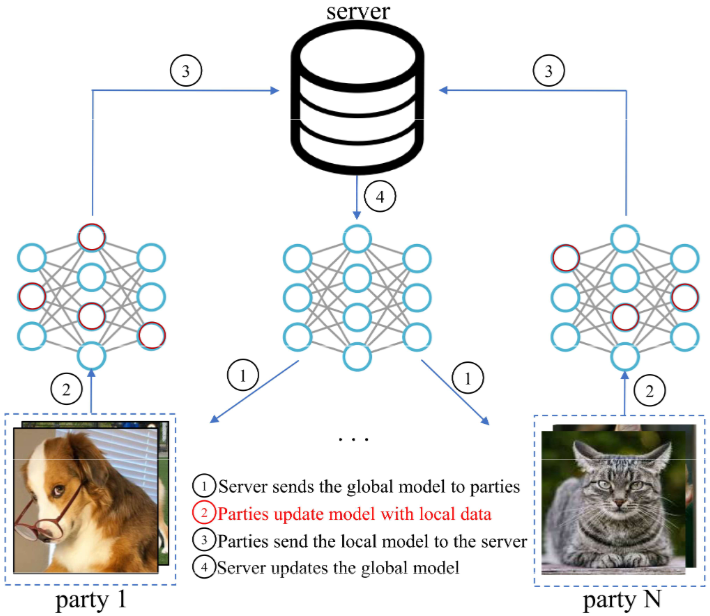
Figure 1. The FedAvg framework. In this paper, we focus on the second step, i.e., the local training phase.

Figure 1은 FedAvg 프레임워크를 보여줍니다. FedAvg는 다음 4단계로 진행됩니다.

(1) 서버가 클라이언트한테 글로벌 모델 전송
(2) 클라이언트들은 SGD 수행하여 locally하게 모델 업데이트
(3) 로컬 모델들을 서버에 전송
(4) 서버는 모델 가중치 평균 내어 다음 라운드 훈련 위한 글로벌 모델 생성

• FedAvg 향상 방법

non-IID한 상황에서 FedAvg를 향상하기 위한 연구들은 2개의 범주로 나눌 수 있습니다.

(1) 로컬 학습 향상 (Figure 1의 2번 과정)
(2) 집계 향상 (Figure 1의 4번 과정)

이 논문은 (1)번 범주에 속해있습니다.

• local training 향상 방법

FedProx는 local training 동안 목적 함수에서 proximal term을 사용합니다.

proximal term은 현재 글로벌 모델과 로컬 모델 사이의 $l_2$-norm distance를 기반으로 계산됩니다.

결국, 로컬 모델의 업데이트는 proximal term에 의해 제한되는 거죠.

SCAFFOLD는 control variates를 통해 로컬 업데이트를 조정합니다.

control variates도 훈련 모델처럼 local training 동안 업데이트 됩니다.

non-iid한 상황에서 FedAvg의 성능을 향상 하기 위해 FedProx와 SCAFFOLD가 등장했지만,
이 두 방법도 이미지 데이터셋에서는 FedAvg 보다 이점이 없었습니다.

• aggregation 향상 방법

FedMA는 Bayesian non-parametric 방법을 사용합니다.

FedAvgM은 서버에서 글로벌 모델을 업데이트할 때 모멘텀을 적용합니다.

FedNova는 평균 전에 로컬 업데이트를 normalize 합니다.

본 논문은 로컬 학습 단계에서 위 방법들과 결합 가능합니다

• personalized FL

각 참여자들을 위해 개인화된 로컬 모델을 학습하는 걸 목표로 하는 연구 분야입니다.

📌 FL의 연구 분야로는 (1) local training 향상, (2) aggregation 향상, (3) personalized FL이 있어요. 본 논문은 (1)번 분야의 연구라고 할 수 있습니다.

2.2. Contrastive Learning

• self-supervised learning

자기지도학습은 최근 핫한 연구 방향입니다. 라벨이 없는 데이터로부터 좋은 표현을 학습하려고 시도하는 분야입니다.

• contrastive learning의 key idea

(1) 같은 이미지에서 다르게 증강된 뷰의 표현 거리 감소

(2) 다른 이미지에서 증강된 뷰의 표현 거리 증가

⇒ positive pair (유사한 건) 가까이, negative pair (다른 건) 멀게!

• NT-Xent

contrastive loss 중 하나

$x_i~,~x_j~,~x_k$: 증강된 이미지, $x_i$와 $x_j$는 동일한 이미지에서 나온 긍정 쌍

$\text {sim} (x_i,~x_k)$: $x_i$와 $x_k$의 코사인 유사도, 범위는 $[-1,~1]$

$\tau$ : 온도 (temperature) 매개변수, 유사도 점수를 얼마나 날카롭게 할지 결정

$\mathbb I_{[k \not = i]}$ : $k \not = i$일 때 $1$, $k=i$일 때 $0$

📌 $\tau$가 커짐 → $\text{sim}(x_i,~x_j) / \tau$는 작아짐 → $\exp \left(\text sim(x_i, ~x_j)/\tau \right)$는 $1$에 가까워짐 ($\because \exp(0)=1$ ) → 분자와 분모가 모두 1에 가까워지므로 유사도 분포가 평탄해짐 → 긍정쌍과 부정쌍의 구분이 어려워짐
즉, $\tau$를 너무 크게 하면 안되고 적당히 작게 해야 효과적입니다.

조금 더 간단히 봐보겠습니다.

• 이해를 돕기 위한 예시

(1) 미니 배치에 4개의 원본 이미지가 있다고 가정하겠습니다. 이를 $I_1,~I_2,~I_3,~I_4$라고 하겠습니다.
(2) 증강된 뷰 생성 : SimCLR은 학습 과정에서 원본 이미지에 대해 서로 다른 두 가지 데이터 증강을 적용합니다.

• $I_1$에서 뷰 $v_{1,1}$과 $v_{1,2}$를 생성합니다.
• $I_2$에서 뷰 $v_{2,1}$과 $v_{2,2}$를 생성합니다.
• $I_3$에서 뷰 $v_{3,1}$과 $v_{3,2}$를 생성합니다.
• $I_4$에서 뷰 $v_{4,1}$과 $v_{4,2}$를 생성합니다.

(3) 미니 배치 구성 : 학습에 사용되는 실제 미니 배치는 이 8개 ($2N=8$)의 증강된 뷰들로 구성됩니다.

• $\left \{v_{1,1},~v_{1,2},~v_{2,1},~v_{2,2},~v_{3,1},~v_{3,2},~v_{4,1},~v_{4,2} \right \}$

(4) 긍정 쌍(positive pairs) : ‘동일한 이미지로부터 생성된 쌍’은 바로 이렇게 같은 원본 이미지에서 나온 두 개의 뷰를 의미합니다. 따라서

따라서 N=4인 경우, 긍정 쌍은 다음과 같습니다.

• $(v_{1,1}, v_{1,2}) 와~ (v_{1,2}, v_{1,1})$
• $(v_{2,1}, v_{2,2}) 와~ (v_{2,2}, v_{2,1})$
• $(v_{3,1}, v_{3,2}) 와~ (v_{3,2}, v_{3,1})$
• $(v_{4,1}, v_{4,2}) 와~ (v_{4,2}, v_{4,1})$

(각 쌍은 순서를 바꿔도 동일한 긍정 관계이므로 두 번 언급될 수 있습니다.)

$x_i$와 $x_j$는 이러한 긍정 쌍 중 하나를 나타내는 일반적인 표기라고 보시면 됩니다.

예를 들어, $(v_{1,1}, v_{1,2})$쌍에 대해 $x_i = v_{1,1}, ~x_j = v_{1,2}$로 놓고 손실 $l_{i,j}$를 계산하는 것입니다. 그리고 분모 $\sum_{k=1}^{2N} \mathbb{I}[k \neq i] \exp(\text{sim}(x_i, x_k)/\tau)$는 앵커 뷰 $x_i(=v_{1,1})$와 미니 배치 내의 나머지 7개 모든 뷰들 $(v_{1,2}, v_{2,1}, v_{2,2}, v_{3,1}, v_{3,2}, v_{4,1}, v_{4,2})$ 각각과의 유사도 합이 되는 것입니다.
최종 손실은 미니 배치 내의 모든 긍정 쌍(위에서 나열된 8개의 순서 있는 쌍)에 대해 계산된 손실 값을 모두 더하여 얻어집니다. 이를 통해 모델은 동일 원본 이미지에서 나온 뷰들의 표현은 가깝게, 다른 원본 이미지에서 나온 뷰들의 표현은 멀게 학습하게 됩니다.

📌 본 논문에서는 지도 학습 세팅에 집중하고, 서로 다른 모델에 의해 학습된 representation들을 비교하기 위해 model-contrastive 학습을 제안합니다.

전통적인 대조 학습은 주로 self-supervised learning (자기 지도 학습) 분야에서 사용됩니다. 자기 지도 학습은 레이블이 없는 대량의 데이터로부터 유용한 데이터 표현 (data representation) 학습하는 비지도 학습 (unsupervised learning)의 한 형태입니다.

기존 대조 학습은 데이터 샘플의 표현을 비교하지만, 본 논문에서는 아이디어를 가져와 모델 수준에 적용한 것입니다.

3. Model-Contrastive Federated Learning

3.1. Problem Statement

참여자 $P_i$는 로컬 데이터셋 $D^i$를 가집니다. 본 논문의 목표는 모델 $w$를 전체 데이터셋 $D$로부터 학습하는 것입니다. 이때 중앙 서버의 도움을 받을거고, raw data는 공유하지 않습니다.

• $L_i(w)$ : 모델 (w)를 사용했을 때 참여자 (P_i)의 경험적 손실을 나타냅니다. '경험적'이란 실제 보유하고 있는 데이터에 기반하여 계산된다는 의미
• $E_{(x,y) \sim D_i} [\dots]$ : 데이터셋 $D_i$에서 무작위로 추출된 데이터 샘플 ($x,y)$에 대한 대괄호 안의 표현식의 기댓값을 의미합니다. 이는 $D_i$에 있는 모든 데이터 샘플에 대해 값을 계산한 후 평균을 내는 것과 같습니다.
• $(x,y) \sim D_i$ : 데이터 샘플 $(x,y)$가 참여자 $P_i$의 로컬 데이터셋 $D_i$로부터 왔음을 나타냅니다. 일반적으로 $x$는 입력 데이터, $y$는 해당 레이블을 의미합니다.
• $\ell_i(w; (x, y))$ : 모델 가중치 $w$를 사용하여 단일 데이터 샘플 $(x,y)$에 대해 계산된 손실 함수 값입니다. 이 손실 함수는 모델 $w$가 입력 $x$에 대해 얼마나 잘못 예측했는지 측정합니다.

📌 이 수식은 참여자 $P_i$가 가진 데이터 $D_i$ 전체에 대해 모델 $w$의 성능을 측정하는 평균 손실 값을 나타냅니다.

3.2. Motivation

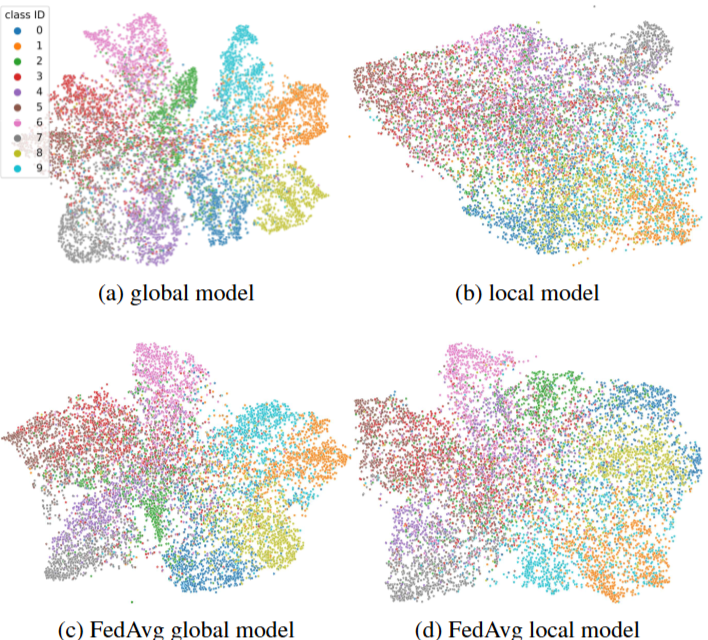
Figure 2. T-SNE visualizations of hidden vectors on CIFAR-10

Figure 2는 전체 데이터셋으로 훈련된 모델이 편향된 부분 집합에서 훈련된 모델보다 더 낫다는 걸 보여줍니다.

Figure 2	설명
(a)	CIFAR-10 데이터셋으로 CNN 모델을 훈련한 뒤, t-SNE를 통해 테스트 데이터셋 이미지의 hidden vector를 시각화한 결과 입니다.
(b)	불균형한 방식으로 데이터셋을 10개의 부분 집합으로 나누고, 각 부분 집합에 대해 CNN을 훈련한 결과 입니다. 모델은 랜덤 하게 선택되었습니다.
(c)	10개의 부분 집합에 대해 FedAvg 적용 결과 입니다. 글로벌 모델이 학습한 표현을 보여줍니다.
(d)	10개의 부분 집합에 대해 FedAvg를 적용하고, 글로벌 모델을 기반으로 훈련된 로컬 모델의 표현을 보여줍니다.

(c)에 비해 (d)에서 동일 클래스에 속하는 점들이 더 넓게 퍼져있습니다. 이는 편향된 로컬 데이터 분산으로 인해, 로컬 학습 단계에서 모델이 더 나쁜 표현을 학습하도록 할 수 있음을 의미합니다.

Figure 2를 통해 우리는 글로벌 모델이 로컬 모델보다 더 나은 특징 표현을 학습한다는 걸 알 수 있습니다.

또한 로컬 업데이트에 $drift$가 있음을 알 수 있습니다.

📌 우리는 non-IID 데이터 상황에서, (1) drift와 (2) 로컬 모델과 글로벌 모델 표현 사이의 간극을 좁혀야 합니다.

3.3. Method

MOON은 FedAvg를 기반으로 하는 간단하고 효과적인 접근법입니다.

MOON의 목표는 다음과 같습니다.
(1) 로컬 모델과 글로벌 모델의 표현 거리 줄이기
(2) 로컬 모델과 이전 로컬 모델의 표현 거리 늘리기

• 3.3.1. Network Architecture

Network는 (1) base encoder, (2) projection head, (3) output layer 총 3개의 컴포넌트로 구성됩니다.

base encoder에서 input으로부터 표현 벡터를 추출하고, projection head에서 고정된 차원에 표현을 매핑합니다. 마지막으로, output layer에서 각 클래스에 대한 예측 값을 생성합니다.

• 3.3.2. Local Objective

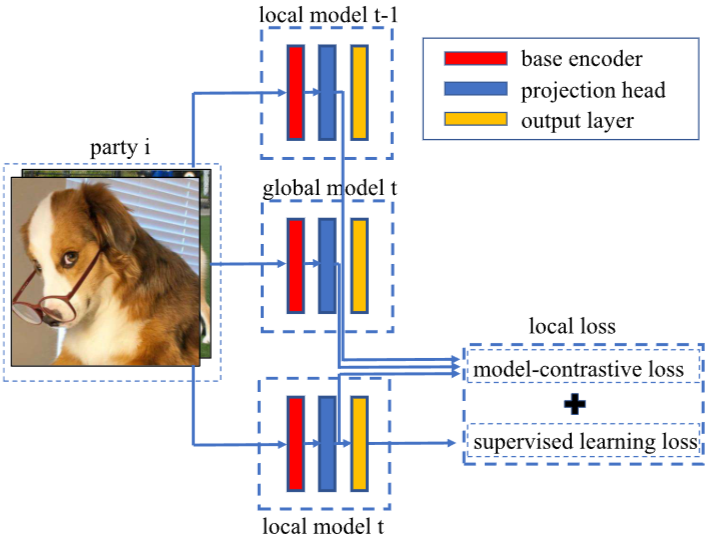
Figure 3. The local loss in MOON

local loss는 2개의 부분으로 구성됩니다.

(1) $\ell_{sup}$ : 지도 학습에서의 전형적인 loss term (e.g., cross-entropy loss)

(2) $\ell_{con}$ : 논문에서 제안하는 model-contrastive loss term

$P_i$는 서버로부터 global model $w^t$를 받아서 로컬 학습 단계를 통해 모델 $w_i^t$를 업데이트 합니다.

모든 입력 $x$에 대해서 글로벌 모델 $w^t$와 이전 라운드의 로컬 모델 $w_i^{t-1}$, 업데이트 된 로컬 모델 $w_i^t$로부터 $x$에 대한 표현을 추출합니다.

📌 글로벌 모델에서 추출한 표현이 더 나으므로, 목표는 $z=R_{w_i^t}(x)$와 $z_{glob}=R_{w^t}(x)$의 거리를 줄이고, $z$와 $z_{prev}=R_{w_i}^{t-1}(x)$의 거리는 증가시키는 것입니다.
즉, 글로벌 모델과의 거리는 좁히고 이전 로컬 모델과의 거리는 늘리는 것입니다.

$R_w(\cdot)$은 output layer 전까지의 네트워크를 의미합니다. 다시 말해서 입력 $x$에 대해 매핑된 표현 벡터입니다.

model-contrastive loss입니다.

글로벌 모델과 로컬 모델의 유사도가 커지는 방향으로 학습하게 됩니다.

입력 $(x,y)$에 대한 loss 계산입니다. 각 참여자는 로컬 데이터셋 전체에 대한 이 loss의 평균을 최소화하려고 합니다.

복잡해 보이지만 지도 학습 손실과 model-contrastive loss를 더해서 총 loss를 구하는 것 뿐입니다.

$\mu$는 model-contrastive loss의 가중치를 조절하는 파라미터입니다. 이 값이 클수록 model-contrastive loss의 영향이 커집니다.

📌 MOON의 로컬 손실 함수는 전통적인 지도 학습 손실에 더해 모델 수준에서의 대조 학습 손실을 추가함으로써, 로컬 모델이 자신의 로컬 데이터를 학습하는 동시에 전역 모델의 좋은 특성을 반영하고 이전 로컬 업데이트의 편향을 극복하도록 설계되었습니다.

주목할 점은 로컬 모델이 충분히 좋고, 글로벌 모델과 (거의) 동일한 표현을 학습하는 이상적인 경우에 model-contrastive loss는 상수가 된다는 것입니다.

로컬 모델이 글로벌 모델과 동일한 표현을 학습하게 되면 $\text {sim}(z, z_{glob})$가 $1$에 가까워지고, 따라서 $\exp()$값이 $e$에 가까워집니다. 결국 $-\log ({e \over e+e})=- \log {1 \over 2}$가 되어 model-contrastive 값이 상수가 되는 것입니다.

이렇게 되면 $\ell = \ell_{sup}(w_i^t;(x,y)) + 상수$와 같아지고, $\ell_{sup}$ (cross-entropy 같은 지도 학습 loss)만 줄이는 방향으로 학습하게 됩니다. 이는 결국 FedAvg의 방식과 동일해짐을 의미합니다.

이를 통해 MOON이 다양한 drift 상황에 관계 없이 강건함을 알 수 있습니다.

3.4. Comparisons with Contrastive Learning

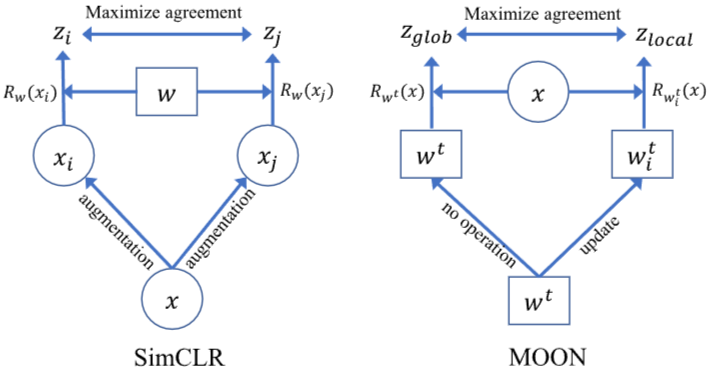
model-contrastive loss는 서로 다른 모델로부터 학습된 표현인 반면, contrastive loss는 서로 다른 이미지로부터 학습된 표현입니다.

MOON은 연합 환경에서 지도 학습을 위한 것이고, 대조 학습은 중앙 환경에서 비지도 학습을 위한 것입니다.

4. Experimets

4.1. Experimental Setup

비교 모델	설명
MOON	본 논문에서 제시한 새로운 방식
FedAvg	가중치들의 평균
FedProx	l2-norm distance 적용해 로컬 업데이트 제한
SCAFFOLD	variance reduction 사용
SOLO	FL 없이 각 참여자들이 로컬 데이터로 학습한 baseline 접근법

데이터셋	설명
CIFAR-10	총 10개의 클래스로 구성된 이미지 데이터셋 일반적으로 60,000개의 32x32 픽셀 컬러 이미지(50,000개 학습, 10,000개 테스트)로 구성
CIFAR-100	총 100개의 클래스로 구성된 이미지 데이터셋 일반적으로 60,000개의 32x32 픽셀 컬러 이미지(50,000개 학습, 10,000개 테스트)로 구성
Tiny-ImageNet	총 200개의 클래스로 구성된 이미지 데이터셋 100,000개 이미지로 구성

네트워크 아키텍처	적용 데이터셋	상세 구조
CNN (base encoder로 사용)	CIFAR-10	5x5 크기 ConV (channel = 6) → 2x2 maxpooling → 5x5 ConV (channel = 16) → 2x2 maxpooling → FC layer (activation = ReLU, units = 120) → FC layer (activation = ReLU, units = 84)
ResNet-50 (base encoder로 사용)	CIFAR-100 Tiny-Imagenet
MLP (projection head로 사용)	all datasets	projection head의 output dimension은 256

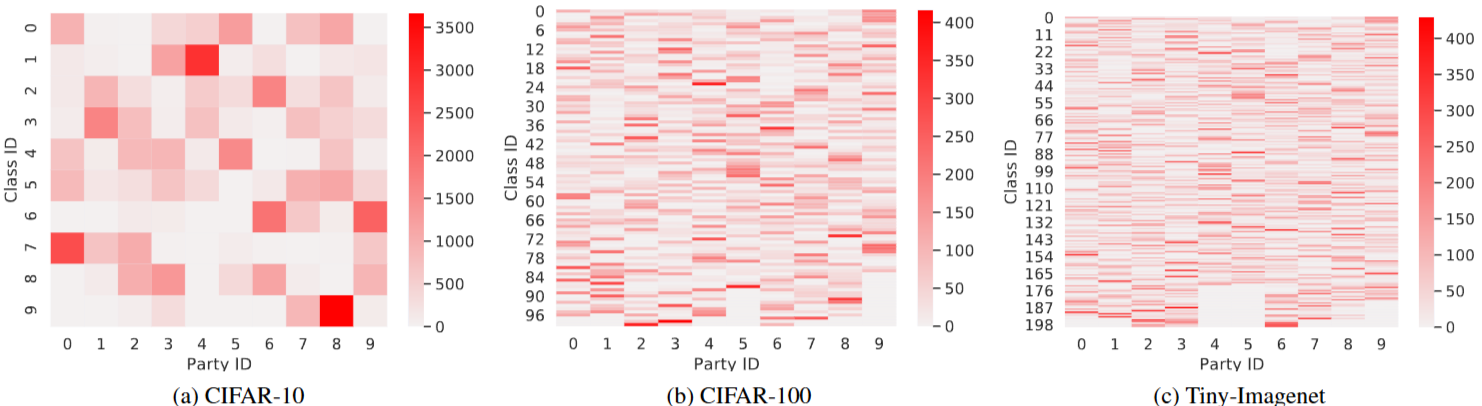
Figure 5. non-IID 데이터 분할을 사용하여 각 party의 데이터 분포를 나타냅니다. 색 막대는 데이터 샘플의 수를 나타냅니다. 각 사각형은 party 내 특정 class의 데이터 샘플 수를 나타냅니다.

4.2. Accuracy Comparison

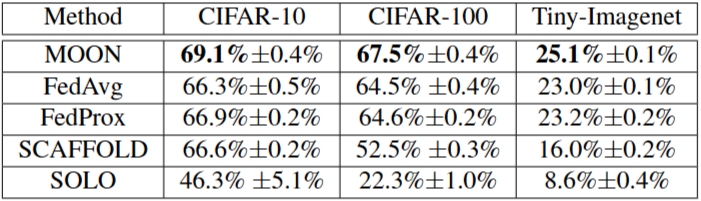
Table 1. MOON과 다른 baselines의 top-1 accuracy. MOON, FedAvg, FedProx 및 SCAFFOLD의 경우, 세 번의 시행을 거쳐 평균과 표준 편차를 보여줍니다. SOLO의 경우, 모든 참여자 간의 평균과 표준 편차를 보여줍니다.

non-IID 환경에서 SOLO는 다른 FL 접근법보다 훨씬 나쁜 정확도를 보여줍니다.

이는 FL을 통해 이점을 얻을 수 있다는 것을 보여줍니다.

4.3. Communication Effciency

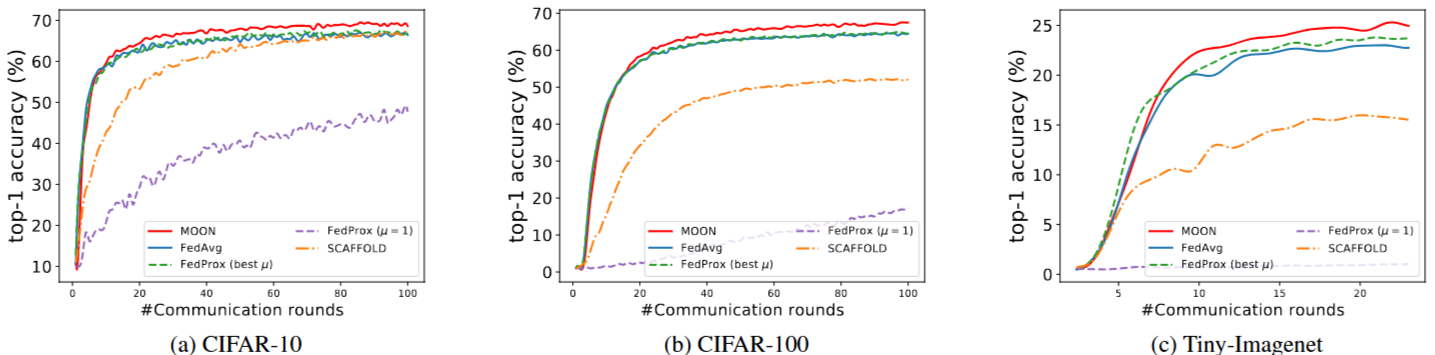
Figure 6. 다양한 통신 라운드 수에서 top-1 테스트 정확도입니다. FedProx의 경우, 최적의 mu를 사용했을 때의 정확도와 mu = 1일 때의 정확도를 모두 보여줍니다.

MOON의 정확도 향상 속도는 초반에는 FedAvg와 거의 동일하지만, 모델-대조 손실(model-contrastive loss)로 인해 나중에 더 나은 정확도를 달성할 수 있습니다.

FedProx에서 알 수 있는 사실은 로컬 모델과 글로벌 모델 사이의 $\ell_2$-norm distance를 제한하는 것은 효과적인 해결책이 아닙니다. 본 논문에서 제시하는 model-contrastive loss는 수렴 속도 감소 없이 정확도를 향상시키는데 효과적입니다.

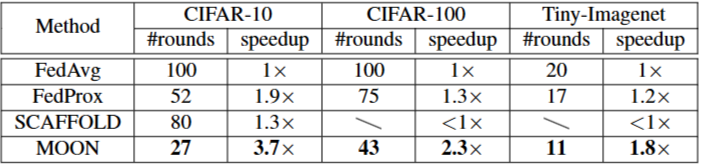
Table 2. 다양한 접근 방식에서 FedAvg를 100라운드 (CIFAR-10/100) 또는 20 라운드 (Tiny-Imagenet) 실행했을 때와 동일한 정확도를 얻기 위한 라운드 수입니다. 접근 방식의 speedup은 FedAvg에 대해 계산됩니다.

MOON에서 통신 라운드 수가 눈에 띄게 감소한 것을 알 수 있습니다. MOON은 FedAvg와 비교했을 때, CIFAR-100과 Tiny-Imagenet에 대해 절반 정도의 라운드가 필요합니다.

MOON은 다른 접근법보다 훨씬 더 통신 효율적입니다.

4.4. Number of Local Epochs

최종 모델의 정확도에 대한 local epoch 수의 영향을 연구합니다.

Figure 7. local epoch 수에 따른 top-1 정확도입니다. MOON과 FedProx의 경우, mu는 모든 local epochs 수에 대해 Section 4.2에서 찾은 최적의 mu로 설정됩니다. SCAFFOLD의 정확도는 local epochs 수가 1로 설정되었을 때 상당히 낮습니다 (CIFAR-10에서 45.3%, CIFAR-100에서 20.4%, Tiny-Imagenet에서 2.6%). Tiny-Imagenet에서 FedProx의 정확도는 local epoch이 1일 때 1.2%입니다.

최종 모델의 정확도에 대한 local epoch 수의 영향을 연구합니다. 결과는 그림 7에 나와 있습니다.

Local epoch 수가 1이면 local 업데이트가 매우 작습니다. 따라서 학습 속도가 느리고 동일한 통신 횟수가 주어지면 정확도가 비교적 낮습니다.

모든 접근 방식은 비슷한 정확도를 보입니다(MOON이 여전히 가장 좋습니다).

Local epoch 수가 너무 커지면 모든 접근 방식의 정확도가 떨어지는데, 이는 local 업데이트의 드리프트 때문입니다.

즉, local 최적점이 global 최적점과 일치하지 않습니다. 그럼에도 불구하고 MOON은 다른 접근 방식보다 확실히 뛰어납니다. 이는 MOON이 부정적인 영향을 효과적으로 완화할 수 있음을 더욱 입증합니다.

4.5. Scalability

MOON의 확장성을 보여주기 위해 CIFAR-100에서 더 많은 수의 참여자를 시도합니다.

구체적으로, 두 가지 설정을 시도하고 있습니다.

(1) 데이터 세트를 50개의 참여자로 분할하고 모든 참여자가 매 라운드마다 연합 학습에 참여한다.

(2) 데이터 세트를 100개의 참여자로 분할하고 매 라운드마다 20명의 참여자를 무작위로 샘플링하여 연합 학습에 참여시킨다 (FedAvg에서 소개된 클라이언트 샘플링 기술).
결과는 표 3과 그림 8에 나와 있습니다.

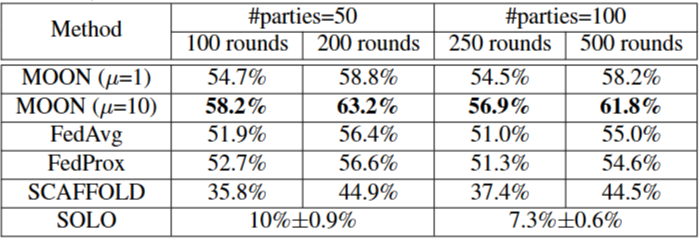
Table 3. CIFAR-100 데이터셋에서 50 참여자와 100 참여자에서의 정확도 (sample fraction = 0.2)

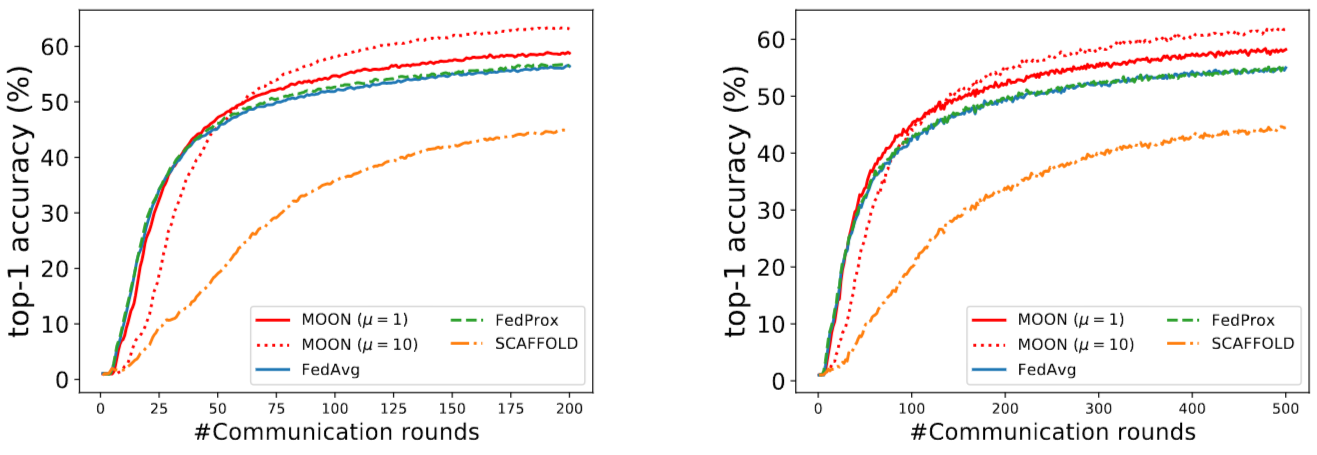
Figure 8. CIFAR-100에서 50/100 참여자에 따른 top-1 test accuracy

MOON의 경우 $\mu = 1$ (4.2절의 최적 $\mu$ 및 $\mu = 10$)의 결과를 보여준다. MOON ($\mu = 1$)의 경우 50명의 참여자로 200라운드에서 2% 이상의 정확도, 100명의 참여자로 500라운드에서 3% 이상의 정확도로 FedAvg 및 FedProx보다 성능이 우수하다.

또한 MOON ($\mu = 10$)의 경우 그림 8에서 볼 수 있듯이 큰 모델-대조 손실로 인해 초기에 학습 속도가 느려지지만 MOON은 더 많은 통신 라운드에서 다른 접근 방식보다 훨씬 뛰어난 성능을 발휘할 수 있다.

FedAvg 및 FedProx와 비교했을 때 MOON은 50명의 참여자로 200라운드에서, 100명의 참여자로 500라운드에서 약 7% 더 높은 정확도를 달성한다. SCAFFOLD는 상대적으로 많은 수의 참여자가 있는 경우 낮은 정확도를 보인다.

4.6. Heterogeneity

본 연구에서는 CIFAR-100 데이터셋에 대해 디리클레 분포의 집중 파라미터 $\beta$를 변경하여 데이터 이질성이 미치는 영향을 연구합니다.

$\beta$ 값이 작을수록 파티션은 더 불균형해집니다. 결과는 표 4에 나와 있습니다.

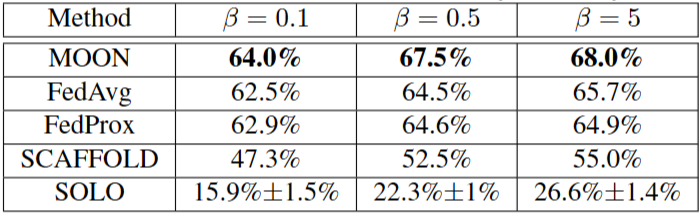
Table 4. beta = {0.1, 0.5, 5}에 따른 테스트 정확도

MOON은 항상 세 가지 불균형 수준에서 가장 우수한 정확도를 달성합니다.

불균형 수준이 감소하면(즉, $\beta = 5$인 경우) FedProx는 FedAvg보다 성능이 떨어지는 반면, MOON은 여전히 FedAvg보다 2% 이상 높은 정확도를 보입니다. 이러한 실험 결과는 MOON의 효과성과 견고성을 입증합니다.

$\beta$가 작을 수록 더 non-iid한 환경이 됩니다.

4.7. Loss Function

표현을 제한하기 위해 다양한 종류의 손실 함수를 사용하는 접근 방식을 비교합니다.

(1) 추가적인 항이 없는 경우 (i.e., FedAvg: $L=\ell_{sup}$)

(2) $\ell_2$ norm $\left(\ell = \ell_{sup} + \mu ||z-z_{glob}||_2 \right)$

(3) model-contrastive loss

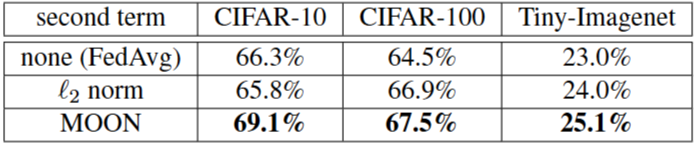
local objective의 두 번째 항에 대한 다양한 종류의 손실에 따른 top-1 정확도입니다. ell_2 norm 접근 방식에 대해 mu를 {0.001, 0.01, 0.1, 1, 5, 10}에서 조정하고 최상의 정확도를 보고합니다.

단순히 $\ell_2$ norm을 사용하는 것은 CIFAR-10에서 FedAvg와 비교했을 때 정확도를 향상시키지 못한다는 것을 알 수 있습니다.

본 논문에서 제안한 model-contrastive loss가 표현 제한에 효과적임을 알 수 있습니다.

model-contrastive loss는 local model에 두 가지 측면에서 영향을 미칩니다.

(1) local model은 global model에 대한 근사 표현을 학습한다
(2) local model은 충분히 좋은 모델이 될 때까지 이전의 표현보다 더 나은 표현을 학습한다

📌 로컬 학습 목적 함수에 더해지는 두 번째 항에 어떤 손실 함수를 사용할 때 성능이 가장 좋은지를 비교하였고, model-contrastive loss가 표현을 효과적으로 제약하고 성능을 향상시키는 데 더 효과적임을 보여줍니다.

Conclusion

non-IID 데이터셋에서 연합 딥러닝 모델의 성능을 향상시키기 위해, 본 논문에서 model-contrastive learning (MOON)을 소개했습니다.

MOON은 model 수준에서의 contrastive learning을 소개했습니다. MOON은 이미지 분류 작업에서 SOTA 접근법입니다.

MOON은 입력값이 이미지가 아니어도 되기에, 향후 non-vision 문제에도 적용될 수 있습니다.