서론
컴퓨터의 기본 단위는 비트이다. 비트는 0과 1, a와 b, 참과 거짓, 흐림과 맑음 처럼 2가지로만 표현가능하다. 비트가 이런 특성을 가지고있기 때문에 컴퓨터는 2진법을 사용하는 것이다.
컴퓨터는 우리가 10진법으로 준 수를 2진법으로 변환해서 이해한다. 2진수에 대한 이해가 있으면 컴퓨터가 우리의 언어를 어떻게 받아들이는지 이해하기 쉬워질 것이다.
2진수는 2를 밑으로 하는 수이다.
10진수는 10을 밑으로 하는 수듯이 2진수는 2를 밑으로 하는 수이다.
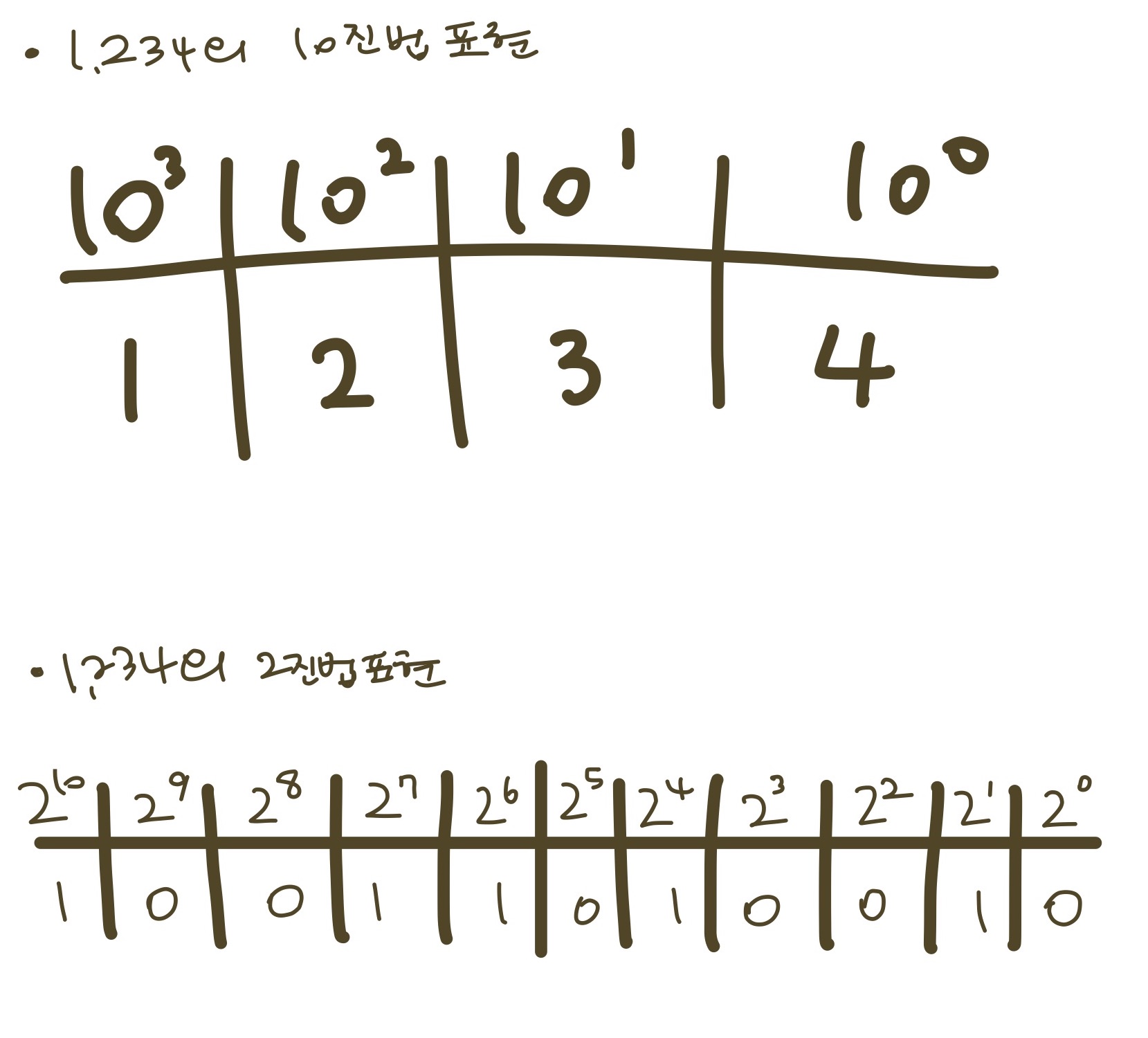
예를 들어 설명해보면 1,234라는 수가 있다. 1234를 10진법으로 표현하면
(1 × 10³) + (2 × 10²) + (1 × 10¹) + (4 × 10⁰) 로 표현할 수 있다.
2진수도 마찬가지이다. 1234를 2진수로 변환하면 10011010010이다.
이 수는
(1 × 2¹⁰) + (0 × 2⁹) + (0 × 2⁸) + (1 × 2⁷) + (1 × 2⁶) + (0 × 2⁵) + (1 × 2⁴) + (0 × 2³) + (0 × 2²) + (1 × 2) + (0 × 2⁰) 로 표현할 수 있다.
즉 11자리 2진수이며 11비트의 수라고 말할 수 있다.
10진수를 2진수로 변환하는 계산법
10진수를 2진수로 계산하는 공식같은 방법이 있다. 이 공식을 그냥 외우면 금방 잊어버리지만 위의 2를 밑으로 표현하는 법을 이해하면 공식도 쉽게 접근할 수 있다.
예를 들어 123이라는 수를 2진수로 변환해보도록 하자. 먼저 가장 가까운 2의 n제곱을 찾아야한다. 2⁶이 64로 가장 가깝다. 123에서 64를 빼준다. 그럼 59가 남는다. 또 59에 가장 가까운 수를 찾는다. 2⁵이 32로 가장 가깝다. 59 - 32를 해준면 27이 남는다. 이런식으로 반복하면 27 - 2⁴ = 11 , 11 - 2³ = 3, 3 - 2¹ = 1 의 과정을 거치게 된다.
결과적으로 2의 n제곱 중 가장 큰 n이 6이기 때문에 123은 2진수로 7자리숫자이다. 사용된 지수의 자리는 1, 사용되지 않은 지수의 자리는 0으로 표시해줄수있고 123은 2진수로 1111011이 된다. 아래 그림을 보면 좀 더 쉽게 이해할 수 있을 것이다.

공식
위 방식으로 계산하려면 계산이 복잡해진다. 많이 사용하는 방법은 몫과 나머지로 변환을 하는 것이다. 변환하려는 수를 2로 나눌 수 있을 때 까지 나누고 마지막 몫을 먼저 적고 나머지들을 역순으로 적어주면 된다.


