Linear Model - Regression
- Linear Model(선형 모델)
-입력 특성에 대한 선형 함수를 만들어 예측을 수행
-다양한 선형 모델이 존재한다
-분류와 회귀에 모두 사용 가능
-
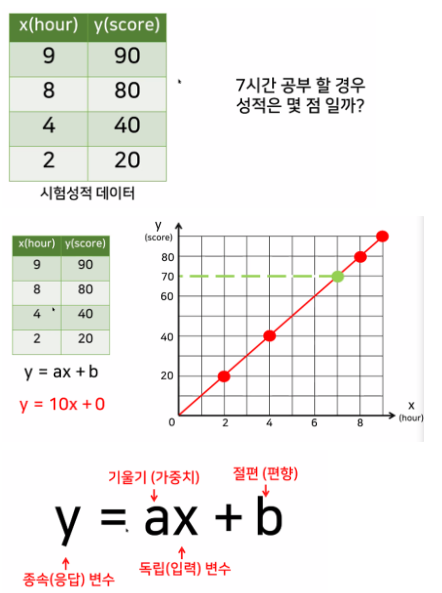
선형 회귀 함수
-
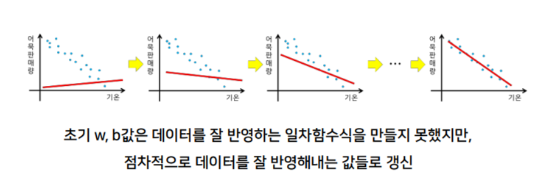
가지고 있는 데이터를 잘 표현할 수 있는 선형 함수 찾기
*모든 데이터를 설명할 수 있는 직선은 없다 -
데이터를 최대한 잘 설명하는 선형 함수 찾기
→ 오차(실제값과 예측값의 차이들의 합, 평균제곱오차(MSE))가 최소가 되는 직선 찾기
→ 가장 좋은 선형 함수
→ 예측 함수로 사용
*선형 함수의 갯수가 무한대이다 -
무한 개의 선형 함수를 계산하지 말고 계산 할 선형 함수의 갯수를 줄여보자(2가지 방법이 존재)
-
- 수학 공식을 이용한 해석적 방법
- 한번에 계산할 공식이 존재
→ 단점 : 공식이 완벽하지 않다 ⇒ 값이 잘못됐을 때 고칠 수 없음
→ 장점: 매우 빠르다
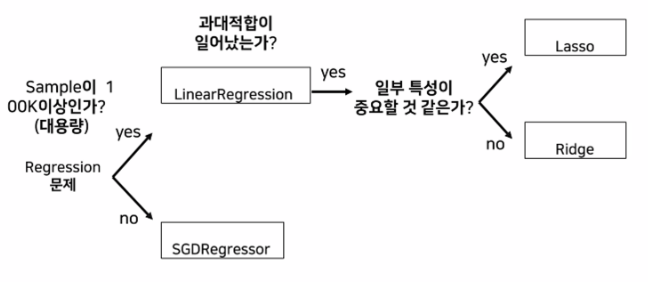
→ 모델 : LinearRegression, Lasso, Ridge
- 경사하강법
- 점진적으로 정답을 찾아간다
→ 단점 : 속도가 느리다
→ 장점 : 값이 잘못됐을 때 고칠 수 있음
→ 모델 : SGDRegressor
⇒ ★ 결론
-
가지고 있는 데이터를 최대한 잘 설명 할 직선 찾기
-
오차를 계산해서 오차가 가장 작은 직선 찾기
-
무한 개의 직선을 계산하지 않고 특정 갯수의 직선만 계산

- Regression(MSE)
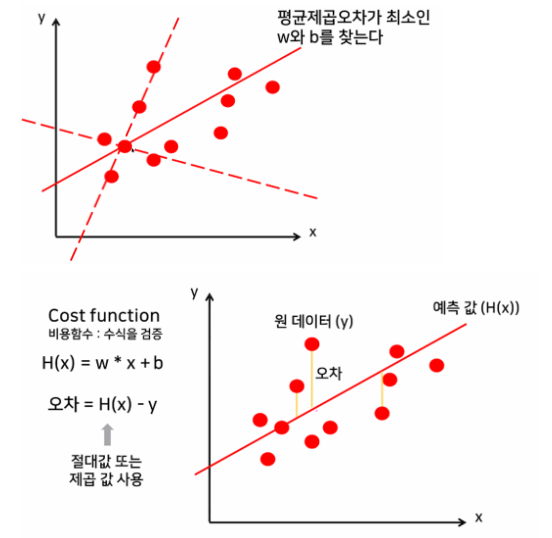
- 평균제곱오차(MSE : Mean Squared Error)
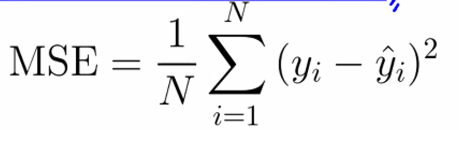
- 평균제곱근오차(RMSE : Root Mean Squared Error)
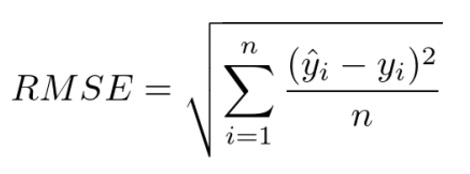
Regression(Gradient descent algorithm)
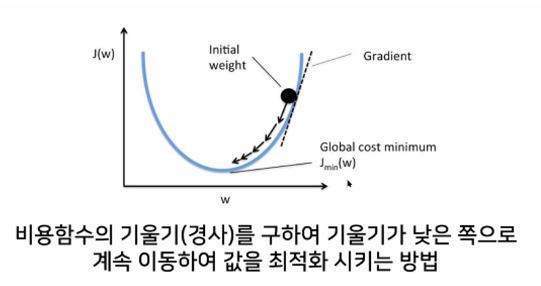
- 경사하강법
점진적으로 정답을 찾아가는 모델
- 주요 매개변수(Hyperparameter)
scikit-learn의 경우

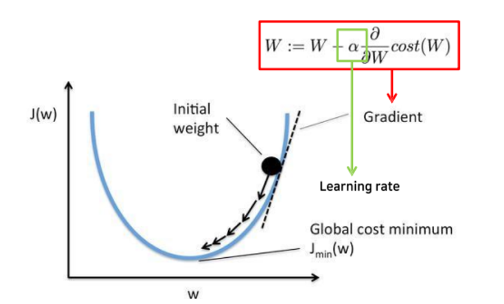
-가중치 업데이트 횟수 : max_iter
-학습률 : eat0
→ 수정을 얼마나 많이 할건지
-
Linear Model 장점
-결과예측(추론) 속도가 빠른다.
-대용량 데이터에도 충분히 활용 가능하다.
-특성이 많은 데이터 세트라면 훌륭한 성능을 낼 수 있다. -
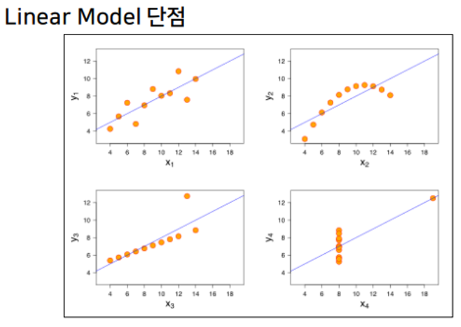
Linear Model 단점
-특성이 적은 저차원 데이터에서는 다른 모델의 일반화 성능이 더 좋을 수 있다. → 특성확장을 하기도 한다.
-LinearRegression Model은 복잡도를 제어할 방법이 없어 과대적합 되기 쉽다. → 모델 정규화(Regularization)을 통해 과대적합을 제어한다.
-
모델 정규화
(Linear Regression : 수학 공식을 이용한 모델 - 결과가 나오면 수정 불가능)
-w가 크다면 입력 x가 조금만 달아져도 y가 크게 변함
-w에 규제를 주어 영향을 줄이도록 하는 것
-L1 규제 : Lasso : 특정 특성이 중요할 때 사용
w의 모든 원소에 똑같은 힘으로 규제를 적용하는 방법
특정 계수들은 0이 됨(0보다 작은 것도 취급 / 0이 된 것들은 사용 X)
특성선택(Features Selection)이 자동으로 이루어진다
-L2 규제 : Ridege : 특성이 골고루 중요할 때 사용
w의 모든 원소에 골고루 규제를 적용하여 0에 가깝게 만든다→ L1, L2 ⇒ Linear Regression + 모델 정규화 - w와 b에 직접적인 수정을 가하는 것
→ Ridge가 더 많이 사용됨 / 보통은 특성이 골고루 중요하다
- 정규화 : cost 함수

- 회귀문제
- RMSE / MSE의 단점
-예측 대상의 크기에 영향을 받음
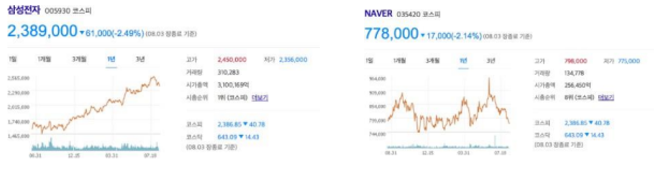
→ 삼성전자와 NAVER의 주가예측 RMSE가 5000이 나왔다면 두 모델의 성능은 동일한가요?
- R2 Score

분류용 선형 모델
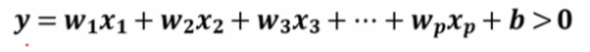
- 특성들의 가중치 합이 0보다 크면 class를 +1(양성클래스)로 0보다 작다면 클래스를 -1(음성클래스)로 분류한다.
- 분류용 선형모델은 결정 경계가 입력의 선형함수
— Logistic Regression(Regression 단어가 붙지만 분류용 모델)
— Linear Support Vector Machine
- 선형 회귀로 풀리지 않는 문제
→ 독립변수와 종속변수가 비선형 관계인 경우
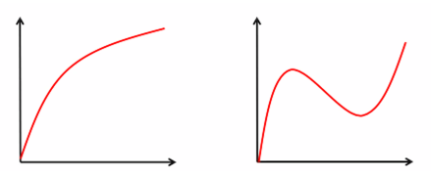
회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘
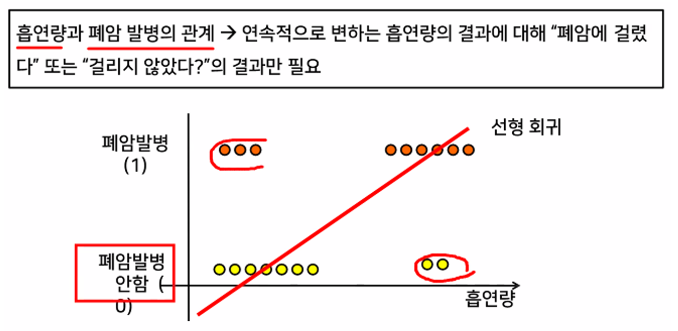
- 선형회귀
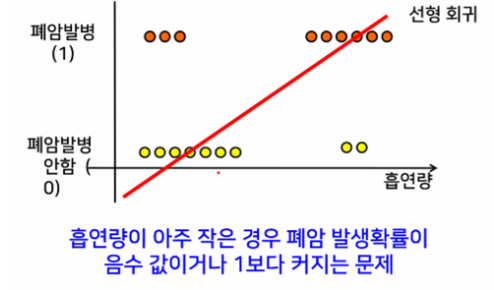
- 해결 방법은?
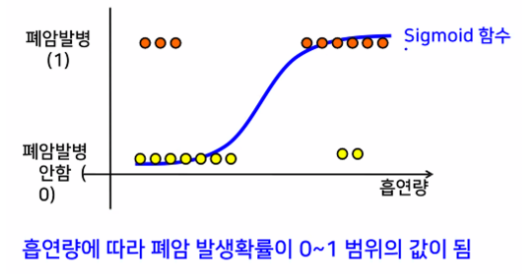
Sigmoid 함수
→ 직선으로 구분할 수 없는 문제 해결
→ 확률이 100%를 넘어가는 문제 해결
Linear Model - Logistic Regression
- 주요 매개변수(Hyperparameter)
sckiti-learn의 경우
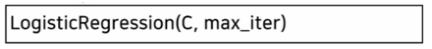
-규제 강도의 역수 : C (값이 작을수록 규제가 강해짐)
-최대 반복횟수 : max_iter (값을 크게 잡아 주어야 학습이 제대로 됨)
-기본적으로 L2규제 사용, 중요한 특성이 몇 개 없다면 L1규제를 사용해도 무방 (주요 특성을 알고 싶을 때 L1 규제를 사용하기도 한다.)
- 공식

Linear Model - SVM
SVM(Support Vector Machines)
- 종이에 선형적으로 분리 가능한 2가지 유형의 포인트가 있다고 가정하면 SV
M은 이 점들을 2가지 유형으로 분리하고 모든 점들로부터 가능한 멀리 위
치하는 직선을 발견 - N차원 장소에서 2가지 유형의 점 집합이 주어지면 SVM은 (N-1) 차원의
초평면(hyperplane)을 생성하여, 이 점들을 두 그룹으로 분리 - 커널이라는 방법을 사용하여 비선형 데이터 분리 → 선형 커널, 다항식 커널
, RBF (Radial Basis Function) 커널 - 마진의 거리가 최대가 되고 마진끼리의 거리가 비슷한 결정 경계 찾기
- 초평면(결정 경계)을 사용하여 데이터를 나눈다.
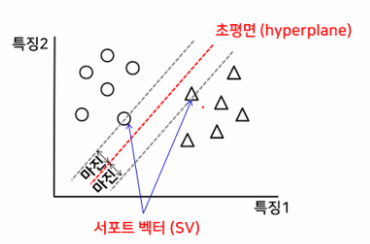
→ 서포트 벡터(SV) : 결정 경계에 가장 가깝게 위치한 데이터
→ 마진 : 결정 경계와 서포트벡터 사이의 거리
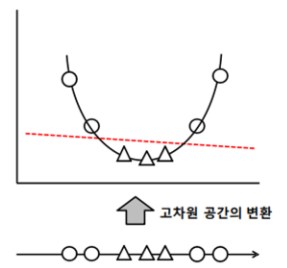
- 커널을 적용한 결정 경계의 변화
from sklearn.linear_model import LogisticRegression
# Sigmoid 함수(S선) 사용 → 직선으로 구분할 수 없는 문제 해결하기 위해서
# 직선을 사용할 때는 확률값이 무한대까지 가는 경향
# Sigmoid직선 사용 → 확률값이 0 ~ 1까지로 제한
# penalty : 규제 선택(11, 12)
# C : 규제의 역수
# max_iter : 반복횟수
lr = LogisticRegression()# 결정 경계를 초평면을 사용
# 서포트 벡터 : 결정 경계와 가장 가까운 데이터
# 마진 : 서포트 벡터와 결정 경계 사이의 거리
# 마진이 최대가 되고, 마진끼리의 값이 비슷해질 수 있는 결정 경계 찾기
from sklearn.svm import LinearSVC
svm = LinearSVC()