📝 오늘 공부한 내용

1. 단변수 함수의 미분과 근사

Linear approximation 선형 근사

• 다항식으로 나타낼 수 없는 (수학적으로 어려운 부분)을 우리가 아는 다항식의 형태로 변환
• 원하는 차수까지 근사 가능하다.
  - 차수가 늘어나면 겹치는 구간도 늘어나게 된다.

2. 다변수 함수의 미분

Partial derivative 편미분

• 한 변수를 제외한 다른 변수들을 상수로 보고 함수의 단변수 미분을 하는 것

Gradient Descent

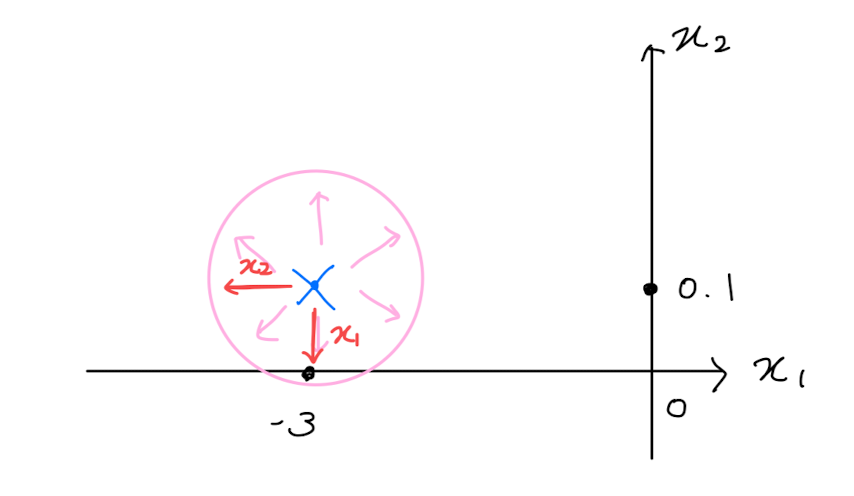
• 반지름의 원 안에서 좌표가 있을 때 가장 값을 감소시키는 곳으로 이동
• 원 안에서는 아무 곳으로 다 움직여도 됨
• 가장 빠르게 증가/감소하는게 loss를 감소할 수 있다.

3. 적분

4. 확률변수

notation과 익숙해지자!

• 확률 변수
• random variable

Probability Mass Function

• 확률 변수의 정의역에 대해서 각 사건이 일어날 확률을 함수로 나타낸 것
• e.g) 동전 - (앞, 뒤) -> PMF -> (0.5, 0.5)
  $Px(X) := P(X=x)$

Probability Density Function

• 연속 확률 변수에서의 PMF를 정의
• CDF를 x에 대해서 미분한 것
  $p(x) := \frac{d}{dx} F(x)$

Cumulative Distribution Function

• -♾️부터 x까지의 범위의 사건이 일어날 확률
  $F(x) = P(X \leq x)$

5. 다양한 확률 분포

이산 확률 분포

연속 확률 분포

6. 다양한 확률 변수

Marginal Distribution

• Joint distribution에서 특정 변수(각각의 변수 하나에 대한)만을 고려한 확률 분포
  구하는 법: x를 구하고자 하면 x외의 다른 값을 누적해서 더해준다

conditional distribution

• marginal과 condition을 더해주면 joint가 나온다

🍩 더 알아둘 것

linearity! 매우 중요

🌷 느낀점 & 오늘 하루

원래 운동을 2시간 했었는데 바뀐 PT 쌤은 2시간이 너무 많다고 했다. (사실 나도 동의)
근력 1시간, 유산소 1시간 했는데 내가 유산소 하는 방식은 아무런 도움이 안된다고 해서 오히려 다행인 느낌?
괜히 재미도 없는 유산소 1시간 탔구나 이런 생각이 들었다 히히...
이제 운동을 1시간 10분 정도 (40분, 30분) 이렇게 하라고 했는데 이렇게 생각하니 훨씬 수월하고 운동을 가고 싶다는 생각이 들었다.

편미분, 단변수 함수, 근사 이런 단어들이 어렵게 느껴졌다 ㅠ.. 영어로 기억해두고 나중에 한국어에 익숙해지는 방식으로 가야될 것 같다.

수학은 역시 문제를 많이 풀어봐야 익숙해질까? 집에가서 실습문제를 한번 더 풀어봐야겠다. 앞으로는 TIL도 꾸준히 적고 열심히 열심히 해야지! 내자신 화이팅 :)