TIL - 2023.09.18

배엘리·2023년 9월 17일

TIL

목록 보기

22/23

날짜를 적고 보니 벌써 9월의 반이 지나갔다.
이렇게 시간이 빠르다니... 17일은 사촌오빠가 놀러와서 공부를 많이 하지는 못했고 밤에 코드만 몇 번 돌려보았다. 오늘은 그동안 사놓고 한번도 안펴본 <밑바닥부터 시작하는 딥러닝> 책으로 부족한 부분만 공부하기로 했다. 이론은 이때까지 배운 부분이랑 비슷해서 이론은 recap느낌으로 갔고 코드만 써보면서 더 익숙해지기로 했다.

🍳 오늘 배운 것

오늘은 밑바닥 2, 3, 4장을 공부했다.

Chapter 2. 퍼셉트론

퍼셉트론이란?

다수의 신호를 입력으로 받아 하나의 신호를 출력

입력 신호가 누련에 보내질 때 가중치가 곱해짐

총 합이 입계값 $\theta$ 을 넘으면 1, 아니면 0

논리회로

AND Gate

모두 다 1일 때 1

NAND Gate

AND의 반대
모두 다 1일 때 0

OR Gate

하나라도 1이면 1

XOR Gate

1이 하나만 있을 때 1

다층 퍼셉트론

퍼셉트론으로는 XOR Gate 표현 불가
- XOR gate는 비선형 역역임
XOR gate는 2층 퍼셉트론
AND, OR, NAND 단층 퍼셉트론 (하나의 직선으로 값들을 분리할 수 있다)

Chapter 3. 신경망

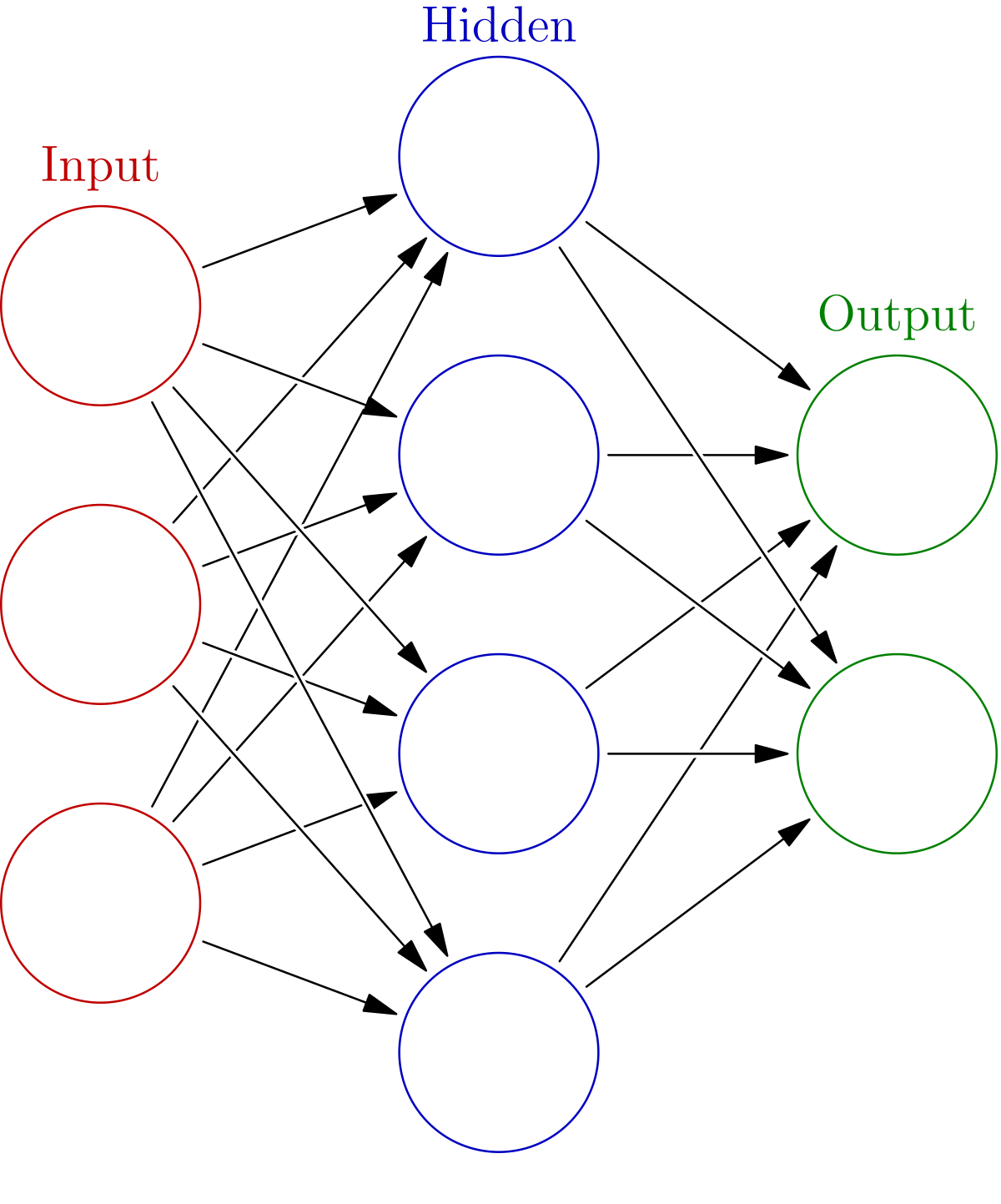
입력층, 은닉층, 출력층

활성화 함수 activation function

입력 신호의 총합을 출력 신호로 변환
$a = b + w_1x_1 +w_2x_2 y = h(a)$
여기서 $h(x)$ 가 활성화 함수

계단 함수

임계값을 경계로 출력이 바뀜

y = h(b + w_1x_1 + w_2x_2)

h(x) = \begin{cases} 0 & \quad (x \leq 0) \\ 1 & \quad (x > 0) \end{cases}

def step_function(x):
    return np.array(x > 0, dtype=np.int64)

그래프를 그려보면,

import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
    return np.array(x > 0, dtype=np.int64)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)

plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()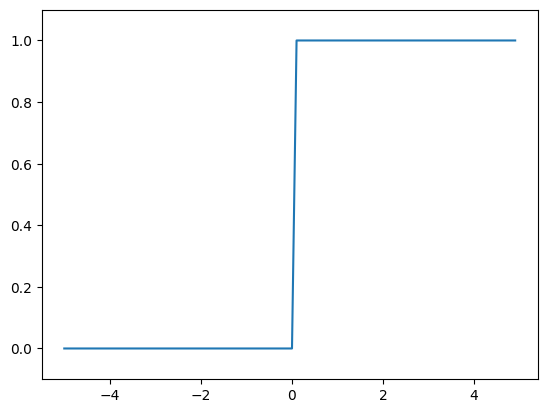

sigmoid 함수

시그모이드는 S자!!!

h(x) = \frac{\mathrm{1} }{\mathrm{1} + \text{exp}(-x) }

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)

plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()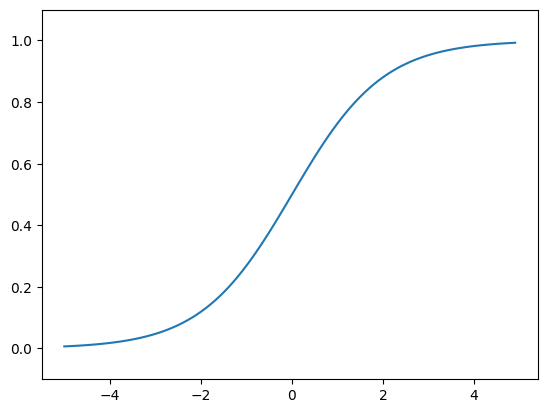

계단 함수와 시그모이드의 차이

계단 함수 0과 1 중 하나의 값
시그모이드는 실수 (연속적인 실수)

ReLU

입력이 0을 넘으면 그 입력을 그대로 (+y 무한대)
0 이하면 0을 출력

def relu(x):
    return np.maximum(0, x)

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)

plt.plot(x, y)
plt.ylim(-0.1, 5.1)
plt.show()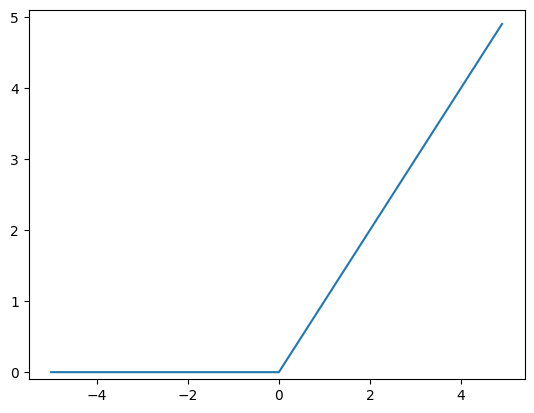

신경망 구현하기

W^{(1)}_{\quad 2\ 3}

이런 가중치가 있다고 했을 때

(1) : 몇 층의 가중치 인지, (1)이니 1층의 가중치

2, 3은 '다음 층 번호, 앞 층 번호' 순으로 적혀 있다.
즉 1층의 3번째 뉴런에서 다음 층인 2층의 2번 뉴런으로 간다

A^{(1)} = XW^{(1)} + B^{(1)}

구현 코드

def init_network():
    network = {}
    X = np.array([1.0, 0.5])
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2,0.4,0.6]])
    network['B1'] = np.array([0.1,0.2,0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['B2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['B3'] = np.array([0.1, 0.2])

    return network

def identity_function(x):
    return x

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    B1, B2, B3 = network['B1'], network['B2'], network['B3']

    A1 = np.dot(X, W1) + B1
    Z1 = sigmoid(A1)
    A2 = np.dot(Z1, W2) + B2
    Z2 = sigmoid(A2)
    A3 = np.dot(Z2, W3) + B3
    y = identity_function(A3) # 출력층으로 나갈 때 항등 함수 (입력을 그대로 출력)

    return y

network = init_network()
X = np.array([1.0, 0.5])
y = forward(network, X)
y

회귀 - 항등 함수 (입력을 그대로 출력)
binary classification - sigmoid
multiclass classification - softmax

softmax

함수의 출력이 0 ~ 1 사이의 실수
출력의 총합 1
출력을 '확률'로 해석

Chapter 4. 신경망 학습

경사 하강법: 손실 함수의 값을 작게 만드는 기법

오차제곱합

E = \frac{1}{2}\sum_{i=1}^{}(y_i-\hat{y_i})^2

$\hat{y_i}$ 는 신경망의 출력 (신경망이 추정한 값)
$y_i$ 는 정답 레이블
$k$ 는 데이터의 차원 수

def sum_squares_error(y, t):
    return 0.5 * np.sum((y-t)**2)

교차 엔트로피 오차

cross entropy error

E = -\sum_{k}^{}y_{k}\log(\hat{y_i})

정답에 해당되는 출력이 커질수록 0에 다가감
출력이 1일 때 0

def cross_entropy_error(y, t):
    delta = 1e-7 # -inf 방지
    return -np.sum(t * np.log(y + delta))

그리고 MNIST 신경망으로 구현하는 것!

🍠 오늘 느낀 점

솔직히 5장까지 한 3시간 안에 끝내겠지.. 이런 생각이 있었는데 지금 새벽 2시죠..?
항상 내가 얼마나 할 수 있는지 간과하는 것 같다. 마라탕집 가면 내가 얼마나 먹을 수 있는지 몰라서 마구잡이로 잡는 것처럼... 그래도 한번 더 코드로 공부하니 그나마 코드가 더 익숙해 진 것 같기도 하고.. 내일은 5장~7장 실습하고 9월 안으로 이 책을 1회독 해보는 걸로!

시간이 많이 부족한 것 같아 불안하기는 하지만 이번 달 내로 책과 기초 머신러닝 코드 공부를 끝내고 10월, 11월부터는 프로젝트랑 실습에 초점을 많이 맞춰야겠다. 내일도 화이팅!

배엘리

이전 포스트

TIL - 2023.09.13

다음 포스트