| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 256 MB | 33197 | 14336 | 10210 | 41.213% |
문제
예제를 보고 규칙을 유추한 뒤에 별을 찍어 보세요.
입력
첫째 줄에 N이 주어진다. N은 항상 3×2^k 수이다. (3, 6, 12, 24, 48, ...) (0 ≤ k ≤ 10, k는 정수)
출력
첫째 줄부터 N번째 줄까지 별을 출력한다.
답안
import math
import sys
def draw_triangle(arr, pos):
x, y = pos
arr[y][x+2] = '*'
arr[y+1][x+1] = arr[y+1][x+3] = '*'
arr[y+2][x] = arr[y+2][x+1] = arr[y+2][x+2] = arr[y+2][x+3] = arr[y+2][x+4] = '*'
def solve(arr, n, k, pos=(0, 0)):
if n == 3:
draw_triangle(arr, pos)
return
x, y = pos
pos_up = (x + 3 * 2**(k-1), y)
pos_left = (x, y + n//2)
pos_right = (x + n, y + n//2)
solve(arr, n//2, k-1, pos_up)
solve(arr, n//2, k-1, pos_left)
solve(arr, n//2, k-1, pos_right)
def print_answer(arr):
for line in arr:
for char in line:
sys.stdout.write(char)
sys.stdout.write('\n')
sys.stdout.flush()
n = int(sys.stdin.readline())
k = int(math.log2(n/3))
arr = [[' ' for _ in range(6*(2**k))] for _ in range(n)]
solve(arr, n, k)
print_answer(arr)풀이
n에 따라 다음과 같은 프랙탈 삼각형을 그리는 문제이다.
예를 들어 만약 n=3이면
*
* *
*****n=6이면
*
* *
*****
* *
* * * *
***** *****n=12이면
*
* *
*****
* *
* * * *
***** *****
* *
* * * *
***** *****
* * * *
* * * * * * * *
***** ***** ***** *****… 와 같이 n의 높이를 가지는 삼각형을 규칙에 맞게 그리면 된다.
n = int(sys.stdin.readline())
k = int(math.log2(n/3))
arr = [[' ' for _ in range(6*(2**k))] for _ in range(n)]문제에서, n은 이다. k의 값을 구해놓는 것이 이후의 계산을 하는 데에 용이하므로, 을 구해놓는다.
그리고 문자열 2차원 배열을 만들고, 초기값을 ‘ ‘으로 설정한다. 앞으로 삼각형을 그릴 필요가 있을 시 배열에 접근하여 업데이트하게 하면 구현에 편리하기 때문이다.
위 삼각형들의 맨 아래 행을 보았을 때 단위 삼각형인
*
* *
*****의 아래 변의 길이가 5칸이고, 각 삼각형들이 공백에 의해 가로 방향으로 띄워져 있어 사실상 삼각형 하나가 차지하게 되는 가로 크기가 6칸이다.
또한, (n=3일 때) k=0, (n=6일 때) k=1, (n=12일 때) k=2, … 등 위 삼각형들의 규칙을 살펴볼 때 가장 아래에 위치하는 단위 삼각형의 개수가 임을 알 수 있다.
따라서 문자열 배열 arr의 세로 크기(높이)는 n, 가로 크기는 으로 설정했다.
이 문제는 단위 삼각형을 그려야 할 때까지 solve 함수를 호출하는 방식으로, 재귀를 이용하여 풀었다.
각 재귀함수에는 문자열 2차원 배열(arr), n, k, 그리고 위치 값을 넘겨준다.
여기서 위치 값이란 삼각형을 그릴 수 있도록 하는 기준점을 말한다.
예를 들어 재귀 깊이가 0일 때 기준점은 다음과 같다. (’O’) 가장 큰 삼각형을 기준으로 했을 때 가장 좌측 상단의 좌표이다.
O *
* *
*****
* *
* * * *
***** *****
* *
* * * *
***** *****
* * * *
* * * * * * * *
***** ***** ***** *****다음으로, 재귀 깊이가 1일 때 기준점은 다음과 같다.
O *
* *
*****
* *
* * * *
***** *****
O * O *
* * * *
***** *****
* * * *
* * * * * * * *
***** ***** ***** *****마지막으로, 재귀 깊이가 2일 때 기준점은 다음과 같으며, 더욱 깊은 재귀 단계로 들어갈 수 없으므로 이 때의 기준점을 중심으로 단위 삼각형을 그린다.
O *
* *
*****
O * O *
* * * *
***** *****
O * O *
* * * *
***** *****
O * O * O * O *
* * * * * * * *
***** ***** ***** *****이때 가장 중요한 부분은 기준점을 어떻게 결정하느냐 하는 것인데, 이것을 코드로 나타낸 부분이 다음과 같다.
pos_up = (x + 3 * 2**(k-1), y)
pos_left = (x, y + n//2)
pos_right = (x + n, y + n//2)pos_up은 한 단계 더 깊은 단계의 위쪽 삼각형이고, pos_left와 pos_right도 역시 한 단계 더 깊은 재귀 단계의 각각 왼쪽과 오른쪽 삼각형이다.
위쪽, 왼쪽, 오른쪽 삼각형의 기준점 좌표는 현재 기준점 대비 각각
만큼 이동한 좌표이다.
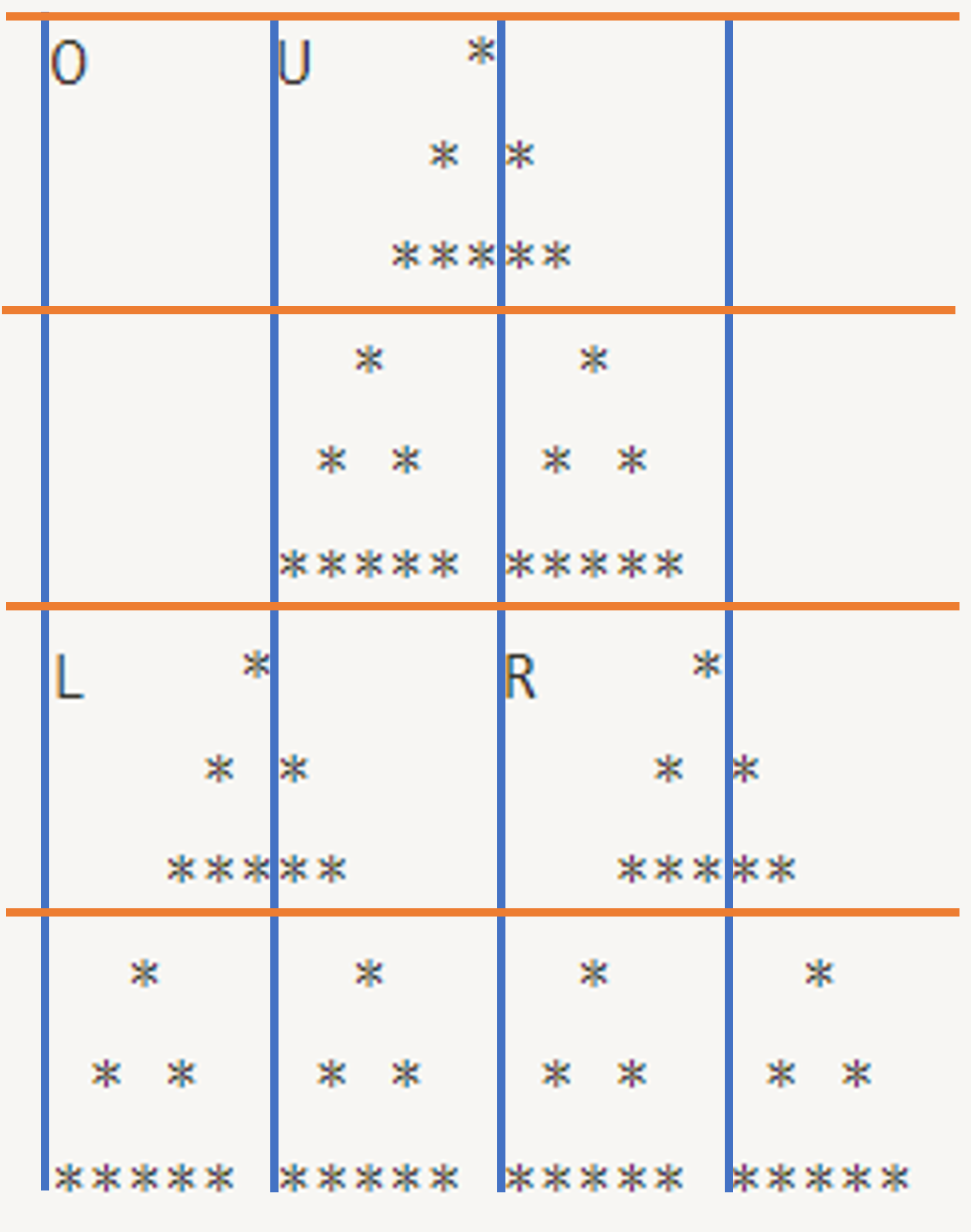
다음과 같이 격자를 그리면 이해가 빠를 것인데, 한 칸의 크기가 가로 , 세로 의 크기를 가지는 격자에서 위쪽 삼각형(U)은 (0,1), 왼쪽 삼각형(L)은 (2,0), 오른쪽 삼각형(R)은 (2, 2)의 위치를 가지게 된다.
solve(arr, n//2, k-1, pos_up)
solve(arr, n//2, k-1, pos_left)
solve(arr, n//2, k-1, pos_right)이렇게 구한 하위 재귀 단계의 삼각형의 기준점 좌표를 다음과 같이 넘겨주면 재귀함수의 구조가 완성된다.
큰 삼각형과 그 다음 단계의 삼각형의 높이를 비교했을 때 높이가 절반이므로 solve 함수의 인자 n으로 2//n을, 더 작은 삼각형이므로 인자 k로 k-1 을 넘겨주면 된다.
이것을 n이 3이 될 때까지 재귀를 수행한 뒤, 마지막 재귀 깊이에서 단위 삼각형을 그린 뒤, 문자 배열인 arr를 출력하면 된다.
