| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 10 초 | 128 MB | 91594 | 43969 | 28536 | 46.672% |
문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
답안
주의: 이 코드는 python3가 아닌 Pypy3로 동작시켰을 때에만 동작합니다.
import sys
def visit(row, col, graph, n):
vertical, diag_upper, diag_lower = graph
vertical[col] = diag_upper[row+col] = diag_lower[row-col+n-1] = True
def visited(row, col, graph, n):
vertical, diag_upper, diag_lower = graph
return vertical[col] or diag_upper[row+col] or diag_lower[row-col+n-1]
def dfs(graph, n, row=0):
global result
for col in range(n):
if not visited(row, col, graph, n):
if row == n-1:
result += 1
return
copied_graph = [graph[0][:], graph[1][:], graph[2][:]]
visit(row, col, copied_graph, n)
dfs(copied_graph, n, row+1)
n = int(sys.stdin.readline())
vertical = [False] * n
diag_upper = [False] * (2*n - 1)
diag_lower = [False] * (2*n - 1)
graph = [vertical, diag_upper, diag_lower]
result = 0
dfs(graph, n)
print(result)풀이
이 풀이에서는 체스 보드의 각 행(row)에 순서대로 queen 한 개씩을 넣는 방식으로 진행한다.
체스의 queen은 그 위치의 가로 줄, 세로 줄, 대각선에 있는 모든 기물을 공격할 수 있기 때문에, 각 행이나 열에 queen 하나씩밖에 들어갈 수 없기 때문이다.
체스 보드의 상태를 저장하기 위해…
vertical = [False] * n
diag_upper = [False] * (2*n - 1)
diag_lower = [False] * (2*n - 1)
graph = [vertical, diag_upper, diag_lower]그리고 이 풀이에서는 queen이 서로 공격 가능한지 판단하기 위해 위 세 개의 리스트를 활용한다.
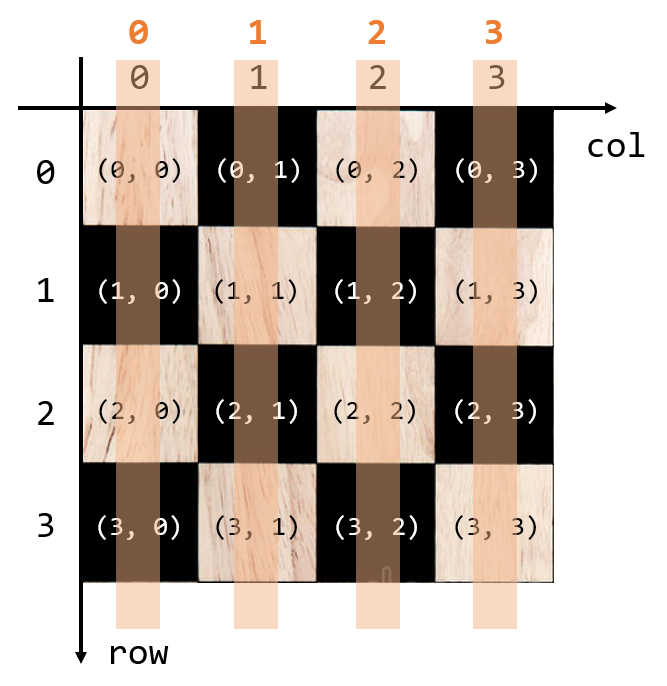
위 그림과 같이, N=4인 체스판이 있다고 해보자.
이때, vertical은 각 열에 queen이 배치되었는지 나타낸다.
예를 들어 N=4일 때, vertical은 [False, False, False, False]와 같은 boolean형 리스트로 나타내어진다.
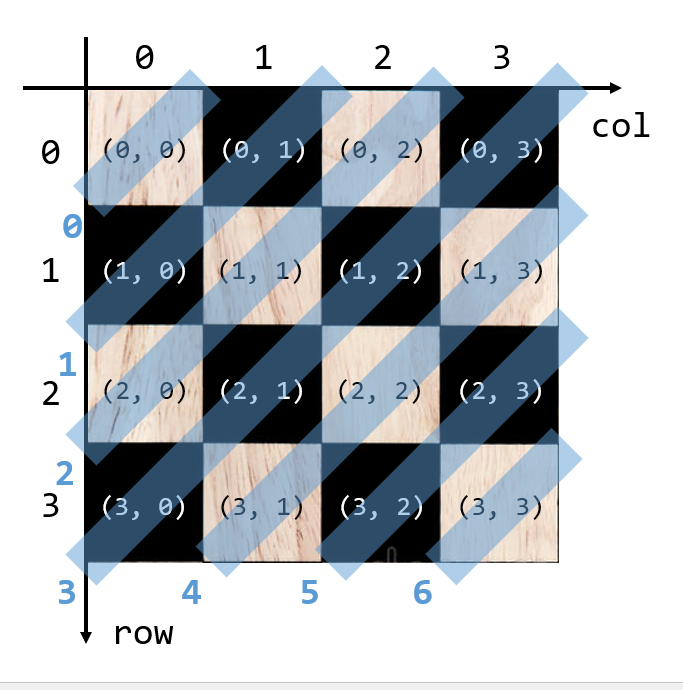
diag_upper는 diagonal_upper의 줄임말으로, 왼쪽 아래에서 오른쪽 위쪽을 향하는 대각선에 queen이 배치되었는지 나타낸다.
예를 들어 N=4일 때, vertical은 [False, False, False, False, False, False]와 같은 boolean형 리스트로 나타내어지고, 각 boolean value는 위 그림의 0, 1, …, 6번 영역을 나타낸다. 이 때 리스트의 크기는 2*N - 1이다.
이때, 각 체스 보드의 x와 y 좌표값만으로 어떤 대각선 영역에 속하는지 알 수 있다.
위 그림의 0번 영역에 속하는 보드 칸들은 x와 y 좌표값을 더한 값이 0이고, 1번 영역에 속하는 보드 칸들은 x와 y 좌표값을 더한 값이 1이고, … n번 영역에 속하는 보드 칸들은 x와 y 좌표값을 더한 값이 n이라는 규칙이 있다.
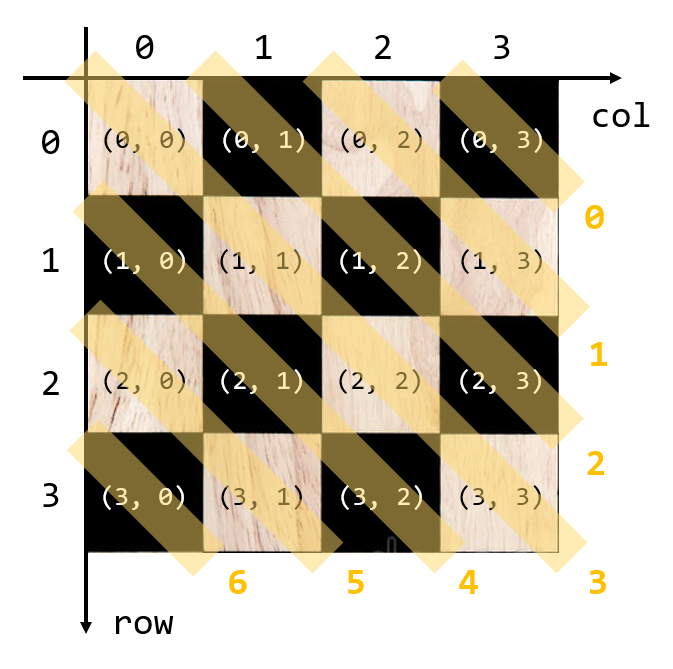
이와 비슷하게, diag_lower는 diagonal_lower의 줄임말으로, 왼쪽 위에서 오른쪽 아래쪽을 향하는 대각선에 queen이 배치되었는지 나타내고, 그 형태는 diag_upper와 같다.
diag_lower도 diag_upper와 비슷하게 규칙성을 가진다.
위 그림의 0번 영역에 속하는 보드 칸들은 x-y+0-1 = 0이 성립하고, 1번 영역에 속하는 보드 칸들은 x-y+1-1 = 1이 성립하고, … N번 영역에 속하는 보드 칸들은 x-y+N-1 = N이 성립한다.
따라서, 만약 (1, 2) 위치에 queen이 배치된다면,
- column 값이 2이므로
vertical[2]= True가 되고, - x 좌표값과 y 좌표값의 합이 1+2=3이므로
diag_upper[3]= True가 되고, - x 좌표값 - y 좌표값 + N - 1 = 1-2+4-1 = 2이므로
diag_lower[2]= True가 된다.
이 세 개의 리스트 vertical, diag_upper, diag_lower로 이뤄진 또다른 상위 리스트 graph를 통해 체스판의 상태를 관리할 수 있다.
코드 로직
def dfs(graph, n, row=0):
global result
for col in range(n):
if not visited(row, col, graph, n):
if row == n-1:
result += 1
return
copied_graph = [graph[0][:], graph[1][:], graph[2][:]]
visit(row, col, copied_graph, n)
dfs(copied_graph, n, row+1)
...
dfs(graph, n)이 코드에서는 재귀적으로 문제가 풀이된다.
0번째 행부터 N-1번째 행까지 순차적으로 queen을 하나씩 배치한다.
queen에 의해 공격이 가능한 지점을 ‘방문되었다’고 간주하여, 이전에 배치한 queen이 공격 불가능한 지점을 ‘방문’한다.
만약 특정 행의 모든 열에서 방문이 불가능한 경우에는 if문 안쪽에 있는 dfs() 함수가 실행되지 않으므로 그 경우에서 분기되는 또다른 경우의 수가 생기지 않고 그 경우의 수의 탐색이 종료된다.
row의 값이 n-1과 같은 것은 이 재귀 함수의 탈출 조건이다. n-1번째 행에 방문 가능한 체스 보드 칸이 있다는 의미이기 때문이다.
0번째 행부터 n-2번째 행까지 방문을 했다면, 이미 n-1개의 queen을 배치한 상태이고, 그에 따라 n-1번째 행에 queen을 배치할 수 있는 경우의 수는 하나밖에 남지 않으므로, 또다른 별도의 처리를 하지 않고, result의 값만을 1 증가시킨 뒤 return한다.
dfs() 안에 사용된 dfs(copied_graph, n, row+1)에서는 parameter로 0번째 행부터 row번째 행까지 queen이 배치되어 있는 체스판 상태와, row + 1을 넘겨주어, dfs() 안쪽에서 호출되는 dfs()에서 row + 1번째 행에 queen을 배치하도록 한다.
이때 주의할 것은 리스트를 deep copy해야 한다는 것인데, shallow copy를 해서 넘겨주게 되면 이전에 graph 내의 vertical, diag_upper, diag_lower 등에 True가 저장된 상태를 그대로 넘겨받게 되어 올바른 결과를 낼 수 없게 된다.
shallow copy를 통해 graph 안쪽의 요소를 적절히 True 또는 False로 바꾸어 graph를 하나로만 관리하는 방법도 있을 것인데, 그에 따른 연산과 구현의 복잡성을 감수해야 할 것이다.
deep copy를 하게 되면 메모리를 과도하게 쓰는 것이 아닌지 우려할 수도 있겠으나,
- int의 크기를 4byte라고 했을 때
graph의 크기는 4 * (N+ (2N - 1) + (2N - 1)) =20N - 8으로, 문제에서 주어진N의 최댓값 14가 입력되는 최악의 경우에도graph객체 하나의 크기는 272byte이다. graph의 개수는 재귀의 가장 깊은 곳까지 갔을 때에 최대이며, 이 때 재귀함수는 최대 N의 깊이를 가지므로, 문제에서 주어진N의 최댓값 14가 입력되는 경우에도 모든graph객체의 크기는 272byte * 15 = 4080byte로(dfs()호출 이전 초기에 만들어지는graph객체까지 포함), 약 4KB정도의 저장공간을 차지한다. 이는 문제의 메모리 제한 128MB과 비교하면 아주 작은 수치이다.dfs()함수가 끝나면 가비지 컬렉터에 의해 시간이 지남에 따라 메모리를 반납하게 되므로, 이전에 사용이 종료된graph객체들이 쌓이지 않는다.
이와 같이 가장 깊은 곳까지 탐색을 진행한 경우 result의 값을 증가시키면, 모든 경우의 수를 셀 수 있게 된다.
deep copy
또한 deep copy를 함에 있어, 시간 초과를 막기 위해 주목해보아야 할 것이 있다.
이 코드에서는 아래와 같이 deep copy를 수행했다.
copied_graph = [graph[0][:], graph[1][:], graph[2][:]]
# (참고) `copied_graph = graph[:][:]`와 같이 코드를 작성하면 shallow copy가 된다.필자는 이 코드를 쓰기 전, python에서 제공하는 copy 모듈의 deepcopy 함수를 사용했다.
import copy
...
copied_graph = copy.deepcopy(graph)copy.deepcopy()는 n차원 리스트에 대해서도 모두 deep copy를 해주기 때문에, 이렇게 해도 답을 얻을 수는 있다.
하지만 이렇게 코드를 제출한 결과 시간 초과가 나고 말았다.
여러번 실험을 거치며 나는 copy.deepcopy()의 성능이 그리 좋지 않음을 알 수 있었다. (2023년 5월 14일 기준)
파이썬에서도 python 3.11 이후로 성능 개선에 주안점을 두고 차후 버전 개발을 하고 있다고 하니 이후 성능이 좋아지는지 기대해보자.
아래는 deep copy를 copy.deepcopy()를 써서 수행한 결과이고, (3회 수행 후 평균 계산)
| N | result | attempt 1 | attempt 2 | attempt 3 | average |
|---|---|---|---|---|---|
| 1 | 1 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 2 | 0 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 3 | 0 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 4 | 2 | 0.10020 | 0.00000 | 0.99800 | 0.366067 |
| 5 | 10 | 0.10320 | 0.12020 | 0.10380 | 0.109067 |
| 6 | 4 | 0.30640 | 0.30890 | 0.31290 | 0.309400 |
| 7 | 40 | 0.10331 | 0.11218 | 0.11122 | 0.108903 |
| 8 | 92 | 0.53851 | 0.47486 | 0.53272 | 0.515363 |
| 9 | 352 | 0.21221 | 0.22518 | 0.22754 | 0.221641 |
| 10 | 724 | 0.98389 | 0.95158 | 0.97300 | 0.969487 |
| 11 | 2680 | 4.93392 | 4.89532 | 4.85310 | 4.894115 |
| 12 | 14200 | 28.45248 | 28.77291 | 26.70263 | 27.976005 |
| 13 | 73712 | 178.20760 | 178.61123 | 201.42855 | 186.082459 |
| 14 | 365596 | 10분 이상 | >600 |
아래는 deep copy를 [graph[0][:], graph[1][:], graph[2][:]]와 같이 리스트 슬라이싱을 써서 수행한 결과이다. 그 이외의 모든 코드와 실행 환경은 동일하다.
| N | result | attempt 1 | attempt 2 | attempt 3 | average |
|---|---|---|---|---|---|
| 1 | 1 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 2 | 0 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 3 | 0 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 4 | 2 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 5 | 10 | 0.00000 | 0.10770 | 0.00000 | 0.035900 |
| 6 | 4 | 0.00000 | 0.00000 | 0.00000 | 0.000000 |
| 7 | 40 | 0.10050 | 0.10010 | 0.00000 | 0.066867 |
| 8 | 92 | 0.10816 | 0.31410 | 0.31970 | 0.247320 |
| 9 | 352 | 0.15999 | 0.12394 | 0.00000 | 0.094643 |
| 10 | 724 | 0.59094 | 0.60674 | 0.62472 | 0.607467 |
| 11 | 2680 | 0.31486 | 0.30059 | 0.30143 | 0.305627 |
| 12 | 14200 | 1.53168 | 1.51978 | 1.52594 | 1.525798 |
| 13 | 73712 | 9.43300 | 8.95402 | 9.53909 | 9.308702 |
| 14 | 365596 | 56.93264 | 111.92330 | 105.21877 | 91.358235 |
이와 같이, 작은 크기의 N에서는 큰 차이를 보이지 않지만, N이 커질수록 훨씬 더 큰 차이를 냄을 확인할 수 있다.
python의 deep copy는 이라고 알려져 있는데 (은 포인터로 이뤄진 compound object들의 개수, 은 compound object 안에 저장된 non-compound object들의 평균 개수이다),
이라는 시간복잡도 자체가 문제가 된다기보다는 copy.deepcopy() 자체가 비효율적으로 구현된 것 같다. 구글에도 이 함수가 왜 이렇게 느리냐는 글들을 몇몇 찾아볼 수 있었다.
나중에 기회가 된다면… python의 contributor가 돼봐야겠다는 생각을 했다.
참조하면 좋을 글
깊은 복사의 방법별 처리 속도
https://codesyun.tistory.com/198
recursive가 아닌 iterative approach로 푼 코드.
https://algodaily.com/challenges/classical-n-queen-problem/python
