문제 설명
프로그래머스의 마스코트인 머쓱이는 최근 취미로 당구를 치기 시작했습니다.
머쓱이는 손 대신 날개를 사용해야 해서 당구를 잘 못 칩니다. 하지만 끈기가 강한 머쓱이는 열심히 노력해서 당구를 잘 치려고 당구 학원에 다니고 있습니다.
오늘도 당구 학원에 나온 머쓱이에게 당구 선생님이"원쿠션"(당구에서 공을 쳐서 벽에 맞히는 걸 쿠션이라고 부르고, 벽에 한 번 맞힌 후 공에 맞히면 원쿠션이라고 부릅니다) 연습을 하라면서 당구공의 위치가 담긴 리스트를 건네줬습니다. 리스트에는 머쓱이가 맞춰야 하는 공들의 위치가 담겨있습니다. 머쓱이는 리스트에 담긴 각 위치에 순서대로 공을 놓아가며 "원쿠션" 연습을 하면 됩니다. 이때, 머쓱이는 항상 같은 위치에 공을 놓고 쳐서 리스트에 담긴 위치에 놓인 공을 맞춥니다.
머쓱이와 달리 최근 취미로 알고리즘 문제를 풀기 시작한 당신은, 머쓱이가 친 공이 각각의 목표로한 공에 맞을 때까지 최소 얼마의 거리를 굴러가야 하는지가 궁금해졌습니다.
당구대의 가로 길이 m, 세로 길이 n과 머쓱이가 쳐야 하는 공이 놓인 위치 좌표를 나타내는 두 정수 startX, startY, 그리고 매 회마다 목표로 해야하는 공들의 위치 좌표를 나타내는 정수 쌍들이 들어있는 2차원 정수배열 balls가 주어집니다. "원쿠션" 연습을 위해 머쓱이가 공을 적어도 벽에 한 번은 맞춘 후 목표 공에 맞힌다고 할 때, 각 회마다 머쓱이가 친 공이 굴러간 거리의 최솟값의 제곱을 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
단, 머쓱이가 친 공이 벽에 부딪힐 때 진행 방향은 항상 입사각과 반사각이 동일하며, 만약 꼭짓점에 부딪힐 경우 진입 방향의 반대방향으로 공이 진행됩니다. 공의 크기는 무시하며, 두 공의 좌표가 정확히 일치하는 경우에만 두 공이 서로 맞았다고 판단합니다. 공이 목표 공에 맞기 전에 멈추는 경우는 없으며, 목표 공에 맞으면 바로 멈춘다고 가정합니다.

위 그림은 친 공이 벽에 맞았을 때의 움직임을 나타낸 그림입니다. 치기 전 공의 위치가 점 A입니다.

위 그림은 친 공이 꼭짓점에 맞았을 때의 움직임을 나타낸 그림입니다. 치기 전 공의 위치가 점 A입니다.
제한사항
- 3 ≤
m,n≤ 1,000 - 0 <
startX<m - 0 <
startY<n - 2 ≤
balls의 길이 ≤ 1,000 balls의 원소는 [a, b] 형태입니다.- a, b는 머쓱이가 맞춰야 할 공이 놓인 좌표를 의미합니다.
- 0 < a <
m, 0 < b <n - (a, b) = (
startX,startY)인 입력은 들어오지 않습니다.
입출력 예
| m | n | startX | startY | balls | result |
|---|---|---|---|---|---|
| 10 | 10 | 3 | 7 | [[7, 7], [2, 7], [7, 3]] | [52, 37, 116] |
답안
import math
def distance(x1, y1, x2, y2):
return (x1 - x2) ** 2 + (y1 - y2) ** 2
def mirrored(ball, startX, startY, m, n):
x, y = ball
if not (x == startX and y < startY):
yield x, -y
if not (x == startX and y > startY):
yield x, y + 2 * (n-y)
if not (x < startX and y == startY):
yield -x, y
if not (x > startX and y == startY):
yield x + 2 * (m-x), y
def solution(m, n, startX, startY, balls):
answer = []
for ball in balls:
min_distance = math.inf
direct_distance = distance(startX, startY, ball[0], ball[1])
for endX, endY in mirrored(ball, startX, startY, m, n):
if (new_distance := distance(startX, startY, endX, endY)) == direct_distance:
continue
min_distance = min(min_distance, new_distance)
answer.append(min_distance)
return answer풀이
“딱 한 번”
당구공을 적어도 벽에 한 번은 맞춘 후 목표 공에 맞힌다고 할 때의 최소 거리를 구하는 문제이다.
문제에서는 ‘적어도 한 번’은 벽에 맞추는 것이 조건이라고 했다.
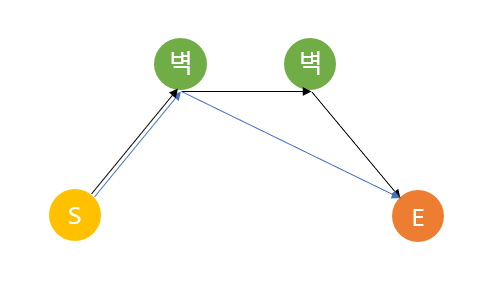
하지만 위 그림에서 볼 수 있다시피, 벽을 두 번 이상 맞춘 뒤 목표 공을 맞히는 것보다, 벽을 한 번만 맞춘 뒤 목표 공을 맞히는 것이 항상 최소이다.
처음 공 위치 → 벽 → 벽 → … → 마지막 공 위치로 이동한다고 했을 때, 위 그림에 화살표로 나타난 경로들은 모두 화살표의 시작과 화살표의 끝을 잇는 최단경로임과 동시에, 주변 장애물 등의 상황에 따라 바뀌지 않는 값이다.
삼각형의 두 변의 길이의 합은 나머지 한 변의 길이보다 길기 때문에, 위의 검은 화살표로 나타난 경로보다 파란색 화살표로 나타난 길이가 항상 짧다.
즉, 이 문제에서는 당구공을 벽에 ‘딱 한 번’ 맞춘 후 목표 공에 맞힐 때의 최소 거리를 구해야 한다.
최단 거리
그 다음으로 생각해보아야 할 것은 어떻게 당구공을 벽에 한 번 맞출 때의 거리를 구하느냐 하는 것이다.
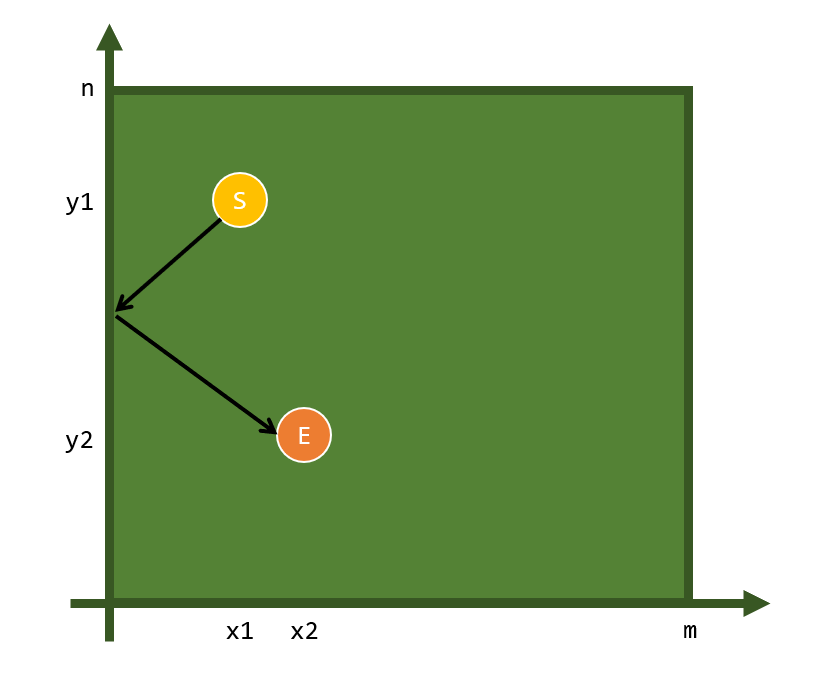
위 그림에서 나타난 경로를 통해 노란색 공을 주황색 공이 있는 위치로 이동시킨다고 해보자.
이때, 문제 조건에서 입사각과 반사각이 같아야 하고 거리가 최소여야 한다.
그러므로 아래와 같이 생각해보자.
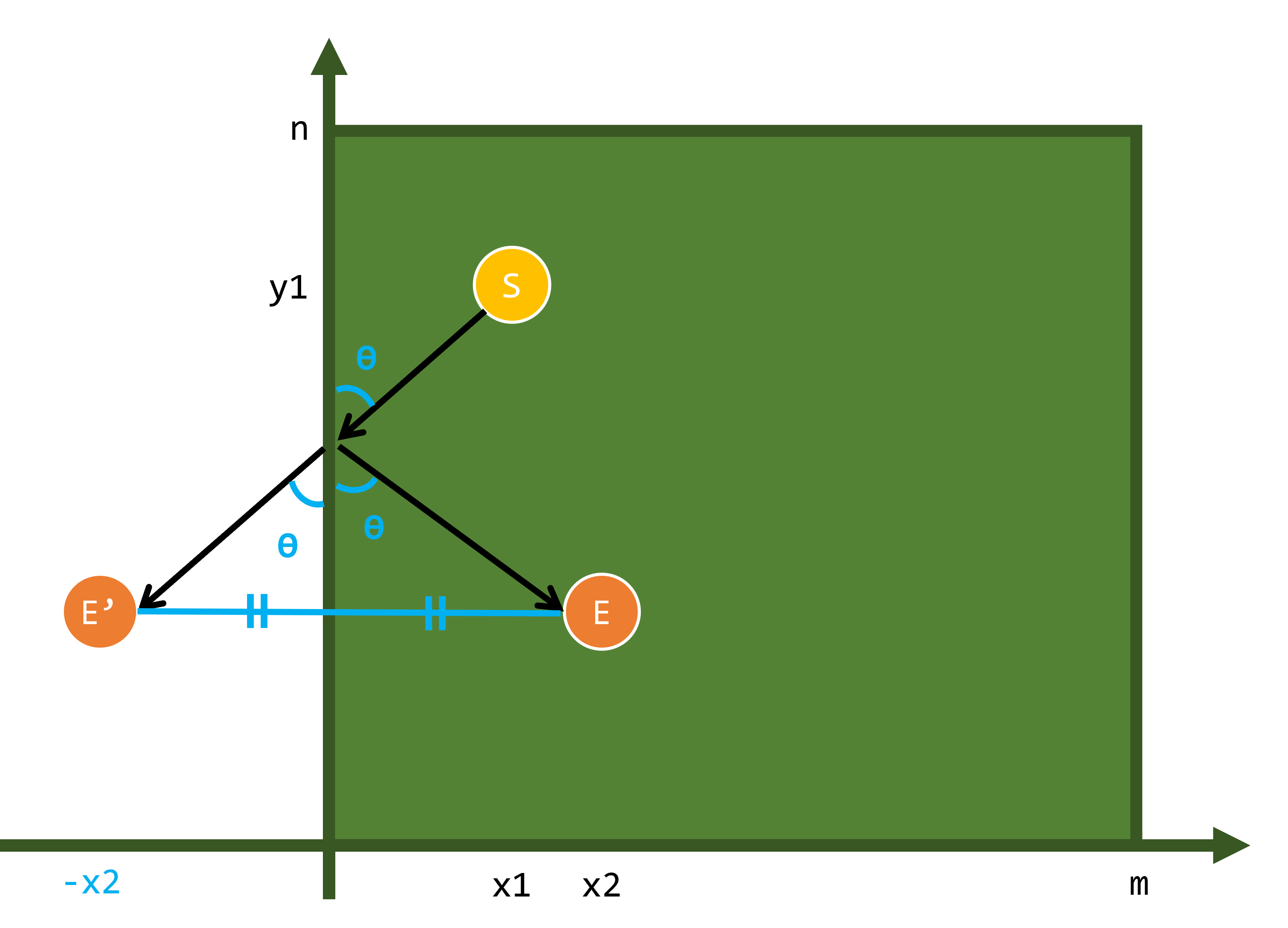
이렇게 주황색 공을 y축에 대해 대칭이동시키면 위 그림에서 만들어지는 두 삼각형은 합동이 되고 (SSS 합동), 이에 따라 얻어지는 효과는 다음과 같다.
벽과E의 길이와벽과E'사이의 길이가 같으므로,S→벽→E’의 거리를 구함으로써S→벽→E의 거리를 구할 수 있게 된다.- 입사각과 반사각이 같아야 한다는 조건을 만족하게 된다.
S공과E'공이 직선으로 이어지게 된다. 즉, 최단 거리로 이을 수 있게 된다.
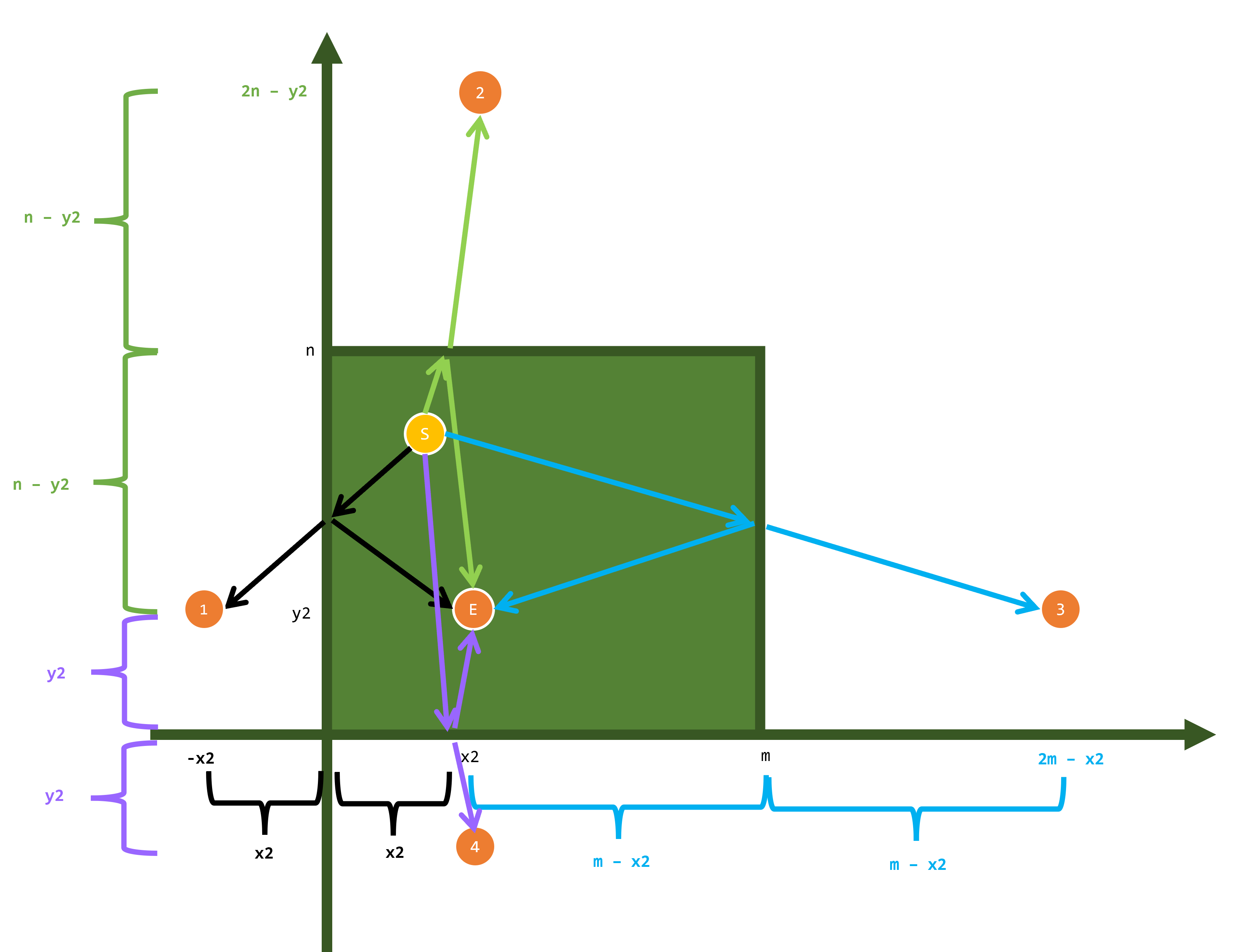
이와 같은 원리를 적용한다면 다음과 같이 각각 왼쪽 벽(검은색), 위쪽 벽(연두색), 오른쪽 벽(하늘색), 아래쪽 벽(보라색)에 충돌 후 목표 당구공을 맞췄을 때 그 목표 당구공이 어디로 대칭이동 하는지 알 수 있다. (각각 1, 2, 3, 4번 공)
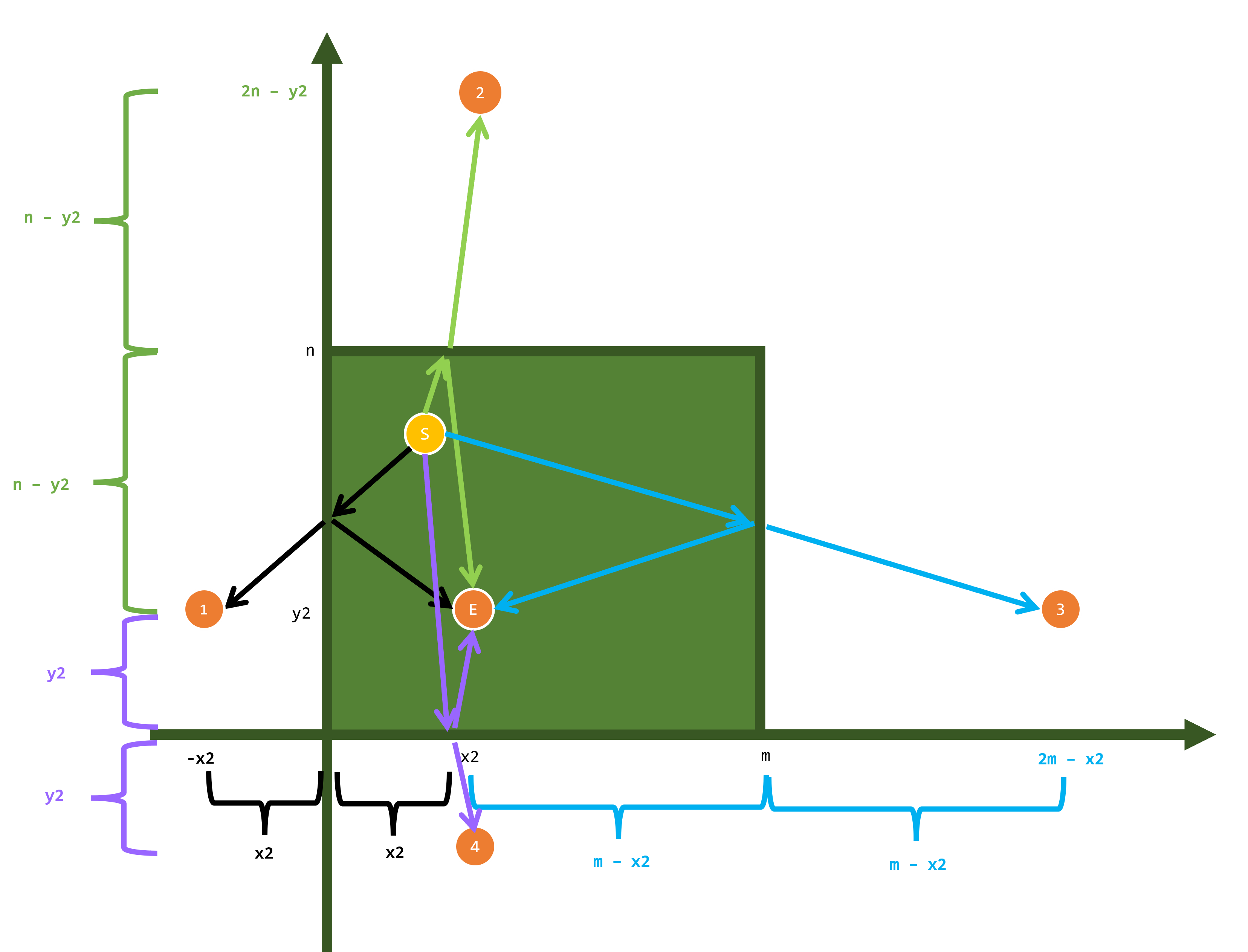
대칭이동된 당구공의 좌표는 목표 당구공의 좌표만으로 알 수 있으므로, 간단히 코드를 짜면 다음과 같이 표현할 수 있다.
import math
def distance(x1, y1, x2, y2):
return (x1 - x2) ** 2 + (y1 - y2) ** 2
def mirrored(ball):
x, y = ball
yield x, -y
yield x, y + 2 * (n-y)
yield -x, y
yield x + 2 * (m-x), y
def solution(balls):
for ball in balls:
min_distance = math.inf
for endX, endY in mirrored(ball, ...):
min_distance = min(min_distance, distance(startX, startY, endX, endY))
answer.append(min_distance)여기서 yield가 잘 이해되지 않는다면 파이썬의 yield, 혹은 generator를 검색해보자.
예외처리
그런데 여기서 예외 처리를 해줘야 하는 곳이 있다.
- 벽과 충돌하기 전 목표 당구공에 충돌하는 경우,
목표 당구공이 벽에 붙어있는 경우
이다.
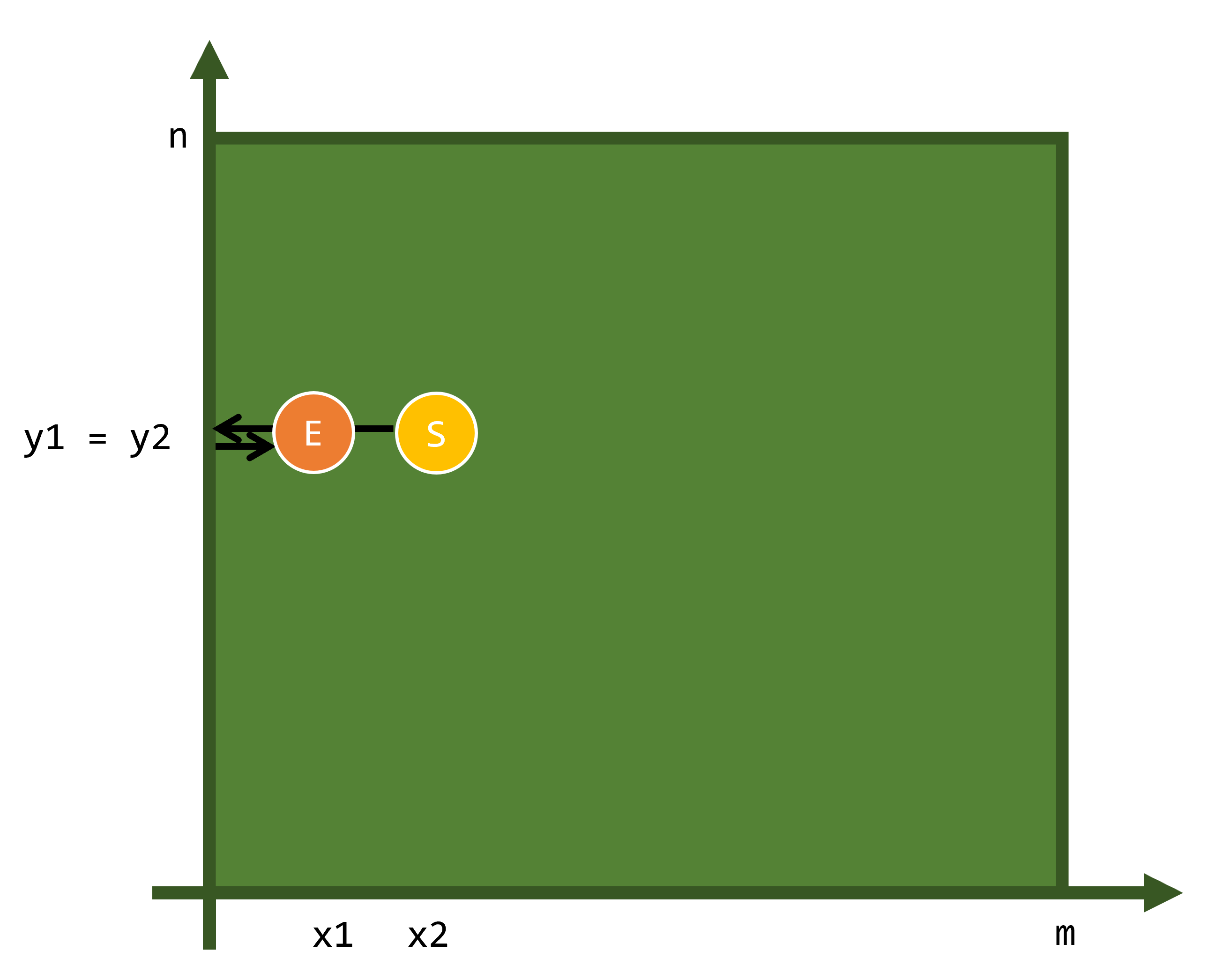
그 중 첫 번째 경우를 보면,
다음과 같이 두 당구공의 y 좌표 값이 같을 때 노란 공을 왼쪽 벽에 충돌시키려고 한다면, 왼쪽 벽에 충돌하기 전에 목표 당구공에 먼저 노란 공이 충돌하여 문제의 조건을 충족시키지 못하게 된다.
따라서
- 다음과 같은 경우에는 아래쪽 벽에 충돌시키면 안된다.
- 두 당구공의 x 좌표가 같음과 동시에,
- 목표 당구공이 시작 당구공과 아래쪽 벽 사이에 위치하는 경우
- 다음과 같은 경우에는 위쪽 벽에 충돌시키면 안된다.
- 두 당구공의 x 좌표가 같음과 동시에,
- 목표 당구공이 시작 당구공과 위쪽 벽 사이에 위치하는 경우
- 다음과 같은 경우에는 왼쪽 벽에 충돌시키면 안된다.
- 두 당구공의 y 좌표가 같음과 동시에,
- 목표 당구공이 시작 당구공과 왼쪽 벽 사이에 위치하는 경우
- 다음과 같은 경우에는 오른쪽 벽에 충돌시키면 안된다.
- 두 당구공의 y 좌표가 같음과 동시에,
- 목표 당구공이 시작 당구공과 오른쪽 벽 사이에 위치하는 경우
위 요구조건을 코드로 표현하면 다음과 같다.
def mirrored(ball, startX, startY, m, n):
x, y = ball
if not (x == startX and y < startY):
yield x, -y
if not (x == startX and y > startY):
yield x, y + 2 * (n-y)
if not (x < startX and y == startY):
yield -x, y
if not (x > startX and y == startY):
yield x + 2 * (m-x), y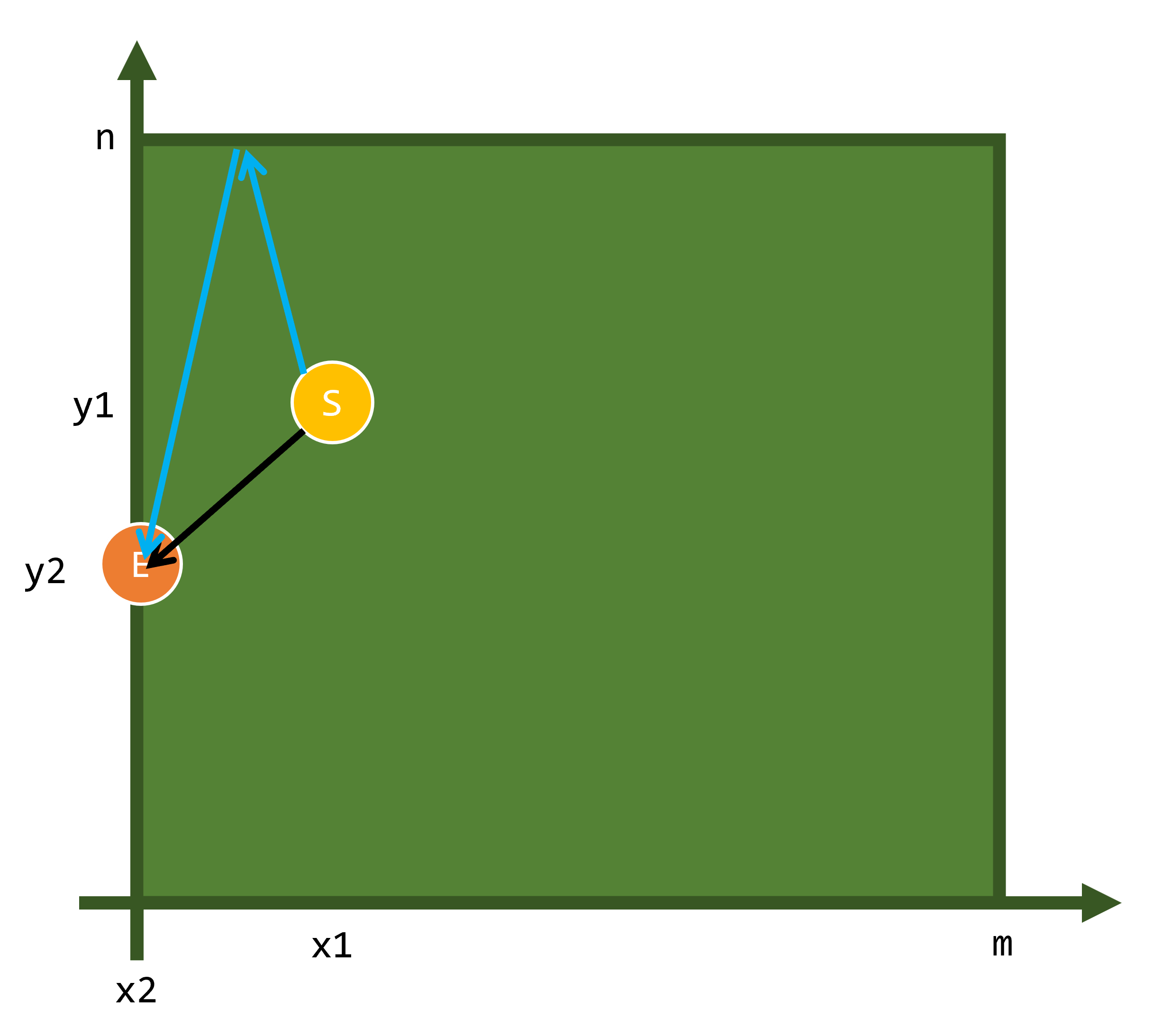
또한 두번째로, 목표 당구공이 벽에 위치하는 경우에 예외처리를 해줘야 한다.
문제에서는 아래와 같이 조건을 제시하고 있다.
공의 크기는 무시하며, 두 공의 좌표가 정확히 일치하는 경우에만 두 공이 서로 맞았다고 판단합니다. 공이 목표 공에 맞기 전에 멈추는 경우는 없으며, 목표 공에 맞으면 바로 멈춘다고 가정합니다.
"원쿠션" 연습을 위해 머쓱이가 공을 적어도 벽에 한 번은 맞춘 후 목표 공에 맞힌다고 할 때,
벽에 맞춘다는 것은 시작 공의 x 좌표값이 0 또는 m이 되거나, y 좌표값이 0 또는 n이 되는 것이므로, 위 그림에서 검은색과 같은 경로로 진행한다면 벽을 맞힌 후에 목표 당구공을 맞히는 것이 아니라, 벽과 목표 당구공을 동시에 맞히는 것이 되어 버리게 된다.
따라서 이와 같은 경로(검은색 화살표)를 제외하고 또다른 최소 경로(파란색 화살표)를 선택하도록 예외처리를 해줘야 한다.
direct_distance = distance(startX, startY, ball[0], ball[1])
for endX, endY in mirrored(ball, startX, startY, m, n):
if (new_distance := distance(startX, startY, endX, endY)) == direct_distance:
continue이러한 예외처리를 위해, 구한 거리가 시작 공과 목표 공을 직선으로 이은 거리와 같을 경우 그 거리를 무시하도록 하였다.
→ balls의 원소인 [a, b]에 대해 0 < a < m, 0 < b < n이므로 예외처리할 필요 없다.
거리를 구할 때, square root를 씌운 euclidean distance ()가 아닌 를 구해야 한다는 점에 유의하며, 각 목표 공까지의 최소 거리들을 저장한 배열을 return하면 정답이 된다.
