그래프 최단 경로 알고리즘 정리 - Dijkstra’s, Bellman-Ford, Floyd-Warshall

Lee Yechan·2024년 1월 9일

Bellman Ford Shortest Path algorithm dijkstra floyd-warshall 그래프 다익스트라 벨만 포드 알고리즘 최단 경로 플로이드 워셜

CS - 알고리즘

목록 보기

1/3

이 글을 쓰게 된 계기

다익스트라, 벨만-포드, 플로이드-워셜…

알고리즘 공부를 조금이라도 해봤다면 못 들어볼 수 없는 이름들이다.

셋 모두 그래프 최단 경로 알고리즘이지만, 다익스트라, 벨만-포드, 플로이드 워셜 알고리즘 각각 모두 특성이 다르고, 그에 따라 활용될 수 있는 곳이 각각 다르다.

알고리즘을 구현할 때마다 항상 헷갈려서 이 글에 아예 정리해 놓으려고 한다.

요약

Single source shortest path (SSSP):
- 벨만-포드 알고리즘
  - 음수 간선 처리 가능, 음수 사이클 처리 불가능
  - 음수 사이클이 있는지 찾아낼 때 활용할 수 있음
  - 시간 복잡도 $O(VE)$
- 다익스트라 알고리즘
  - 음수 간선 처리 불가능
  - 가중치가 없는 그래프의 경우 BFS와 같음
  - 시간 복잡도 $O(V+E \log E)$
All pair shortest path (APSP)
- 플로이드-워셜 알고리즘
  - 음수 간선 처리 가능, 음의 사이클 처리 불가능
  - 시간 복잡도 $O(V^3)$

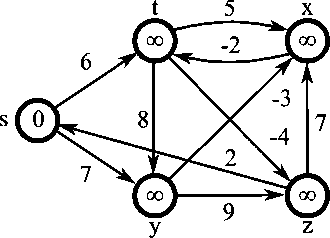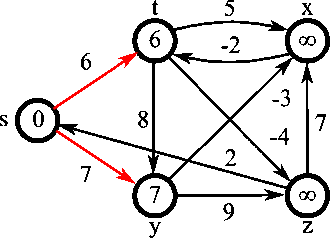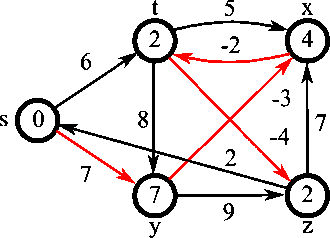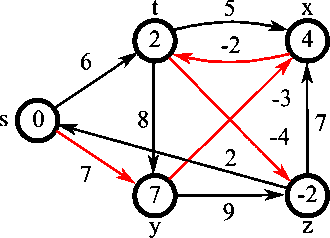
벨만-포드 알고리즘

Single source shortest path 알고리즘, 즉 특정한 시작 노드부터 다른 모든 노드로 가는 최단 경로를 구하는 알고리즘이다.

가중치가 음수인 간선을 처리 가능하지만, 그래프에 길이가 음수인 사이클이 포함된다면 이 알고리즘을 사용할 수 없다.

핵심 아이디어

모든 간선을 살펴보고, 그 간선이 거리를 줄이는 데 사용될 수 있는지 확인한다.

더는 줄일 수 있는 값이 없을 때까지 이를 반복한다.

구현

// edges: (a, b, w), 노드 a에서 b로 향하는 가중치가 w인 간선들을 저장한 배열
// distance: 노드 x에서 각 노드로 향하는 거리를 저장한 배열
for (int i-1; i<=n; i++) {
	distance[i] = INF;
}
distance[x] = 0;
for (int i=1; i<=n-1; i++) {
	for (auto e: edges) {
		int a, b, w;
		tie(a, b, w) = e;
		distance[b] = min(distance[b], distance[a]+w);
	}
}

알고리즘은 V-1번의 라운드로 구성되고, 라운드마다 E개의 간선 모두를 처리한다.

음수 사이클이 있는지 찾아내기

벨만-포드 알고리즘을 V번의 라운드로 진행한다.

만약 마지막 라운드에서도 거리가 줄어드는 경우가 있다면, 그래프에 음수 사이클이 있다고 판단한다.

다익스트라 알고리즘

Single source shortest path 알고리즘, 즉 특정한 시작 노드부터 다른 모든 노드로 가는 최단 경로를 구하는 알고리즘이다.

벨만-포드 알고리즘보다 조금 더 효율적이다.

가중치가 음수인 간선은 처리 불가능하다.

핵심 아이디어

벨만-포드와 같이 탐색 과정에서 거리값을 계속 줄여나가는 것은 동일하나,

가중치가 음수인 간선이 없다는 사실을 이용해 모든 간선을 단 한번씩만 처리한다.

아직 처리하지 않은 노드 중 거리가 가장 작은 노드를 찾고, 그 노드에서 시작하는 모든 간선을 살펴보며 다른 노드까지의 거리를 줄일 수 있다면 줄인다.

거리가 최소인 노드를 찾기 위해 우선순위 큐가 사용된다.

구현

// adj: 인접 리스트. adj[a] = (b, w)
// distance: 노드 x에서 각 노드로 향하는 거리를 저장한 배열
priority_queue<pair<int,int>> q;
for (int i=1; i<=n; i++) {
	distance[i] = INF;
}
distance[x] = 0;
q.push({0, x});
while (!q.empty()) {
	int a = q.top().second; q.pop();
	if (processed[a]) continue;
	processed[a] = true;
	for (auto u: adj[a]) {
		int b = u.first, w = u.second;
		if (distance[a]+w < distance[b]) {
			distance[b] = distance[a]+w;
			q.push({-distance[b], b});
		}	
	}
}

모든 노드를 살펴보며 진행한다.

각 라운드마다, 해당 노드에 연결된 모든 간선에 대해 거릿값을 한 번씩만 우선순위 큐에 추가한다.

음수 간선이 있다면, 결과가 잘못될 수 있다.

플로이드-워셜 알고리즘

All pair shortest path 알고리즘, 즉 모든 노드 간 최단 경로를 구할 수 있는 알고리즘이다.

핵심 아이디어

각 라운드마다 각 경로에서 새로운 중간 노드로 사용할 수 있는 노드를 선택하고 거리를 줄이는 과정을 반복한다.

구현

// dist: 노드 i와 j간의 최단 거리를 나타낸 이차원 배열.
// 배열 내에는 서로 같은 노드 간의 거리는 0, edge가 존재하면 weight, 그밖에는 INF가 저장됨
for (int k=1; k<=n; k++)
	for (int i=1; i<=n; i++)
		for (int j=1; j<=n; j++)
			dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j]);