최소 신장 트리(MST) 알고리즘 정리 - Kruskal's, Prim's

Lee Yechan·2024년 1월 30일

Kruskal's Algorithm MST Minimum Spanning Tree Prim's algorithm Spanning Tree algorithm 신장 트리 최소 신장 트리 크루스칼 프림

CS - 알고리즘

목록 보기

2/3

이 글에서는…

최소 신장 트리가 무엇인지 정리한다.
최소 신장 트리를 구하는 알고리즘(크루스칼, 프림)의 원리와 구현 방법을 정리한다.

최소 신장 트리

신장 트리(spanning tree)란, 어떤 그래프의 부분 그래프로, 그래프의 모든 노드와 간선 일부를 포함하며 모든 노드 간에 경로가 존재하는 것을 말한다. 신장 트리는 연결 그래프이며 사이클이 없다.

예를 들어, 다음 그림에 나와 있는 원래의 그래프는 아래와 같은 여러 개의 신장 트리를 가질 수 있다.

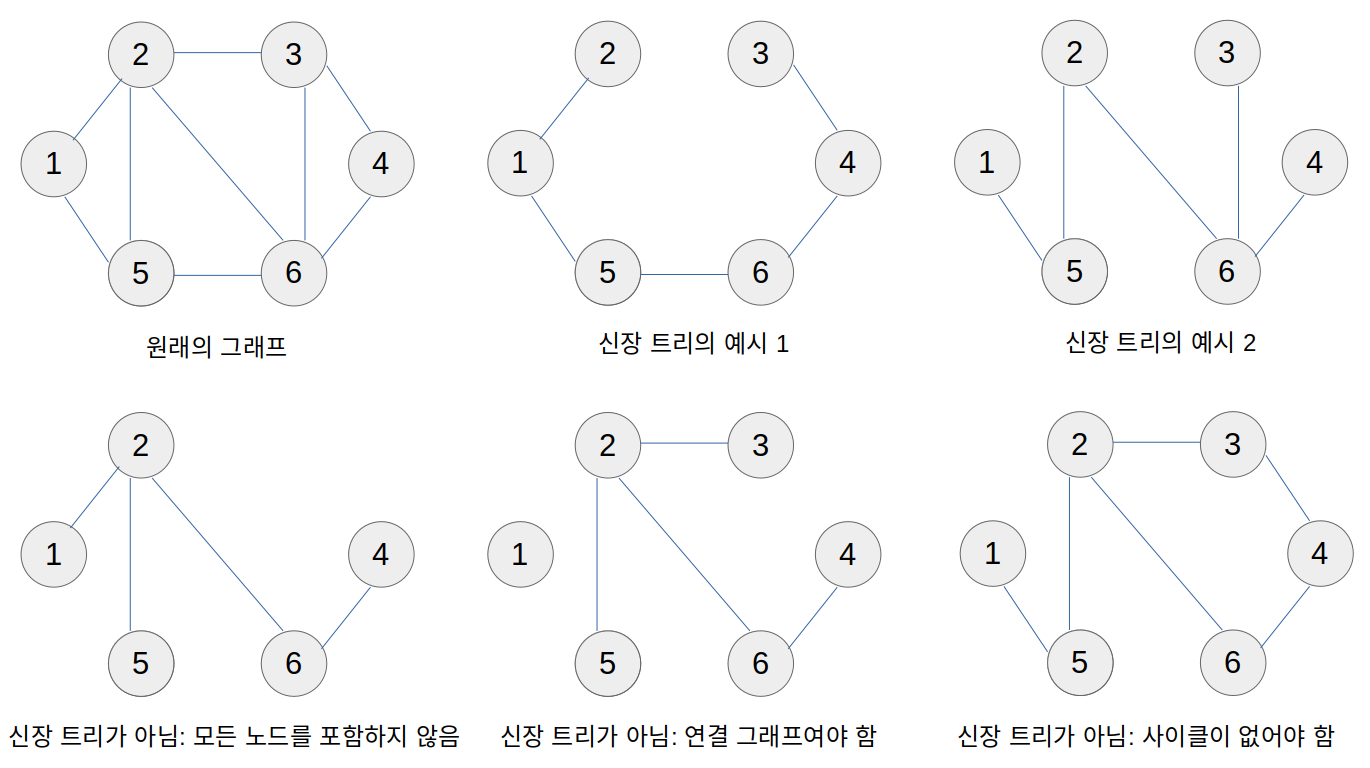
이때 신장 트리의 가중치는 그 신장 트리의 간선 가중치의 합이다.

신장 트리 중 그 가중치가 가장 작은 것을 최소 신장 트리(MST; minimum spanning tree)라고 한다.

한 그래프에 대한 최소 신장 트리는 유일하지 않으며, 여러 개 존재할 수 있다.

어떠한 그래프가 주어졌을 때, 최소 신장 트리를 구하는 알고리즘 중 대표적인 것으로 크루스칼 알고리즘(Kruskal’s algorithm)과 프림 알고리즘(Prim’s algorithm)이 있다.

두 알고리즘은 모두, 아무 것도 없는 상태에서 간선 또는 노드를 하나씩 선택해 최소 신장 트리를 만드는 방법이다.

크루스칼 알고리즘

크루스칼 알고리즘은 간선 선택을 기반으로 하는 알고리즘이다.

노드만 존재하고, 간선이 하나도 없는 그래프의 상태에서, 작은 가중치를 가지는 간선부터 차례대로 추가하여 최소 신장 트리를 만든다.

크루스칼 알고리즘의 작동 방식을 세줄 요약하면 다음과 같다.

노드만 존재하고, 간선이 하나도 없는 그래프에서 시작한다.
작은 가중치를 가지는 간선부터 차례대로 간선을 추가한다.
이때, 사이클이 생기지 않아야 한다.

예시

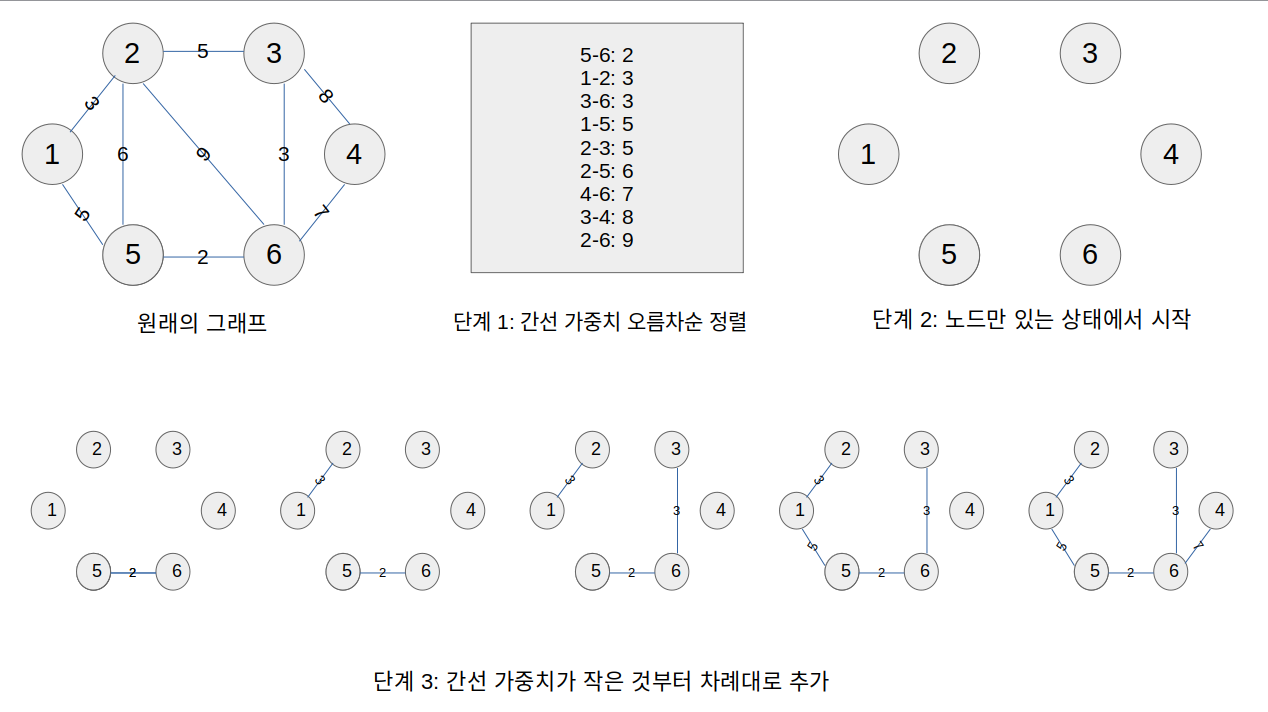
예시 그림에 대한 설명

간선을 가중치 기준으로 오름차순 정렬한다.

간선은 없고, 노드만 있는 상태에서 시작한다.

간선이 가장 작은 것부터 차례대로 추가한다. 이때, 간선을 추가함> 으로써 그래프에 사이클이 생기게 하면 안 된다.

간선 5-6을 잇는다 (가중치 2).

간선 1-2를 잇는다 (가중치 3).

간선 3-6을 잇는다 (가중치 3).

간선 1-5를 잇는다 (가중치 5).

간선 2-3이나 간선 2-5를 추가하면 사이클이 생기므로 무시한다.

간선 4-6을 잇는다 (가중치 7). 간선 V-1개를 추가하여 MST가 만들어졌으니 종료한다.

그리디, 왜 성립하는가?

크루스칼 알고리즘에서 탐욕법 기반의 전략으로 가장 작은 간선을 계속 선택했다.

그런데 이런 방법으로 항상 최소 신장 트리를 구할 수 있다는 것을 어떻게 보장할 수 있을까?

그래프의 간선 중 가중치가 가장 작은 간선이 신장 트리에 포함되지 않는 경우에도 언제나 신장 트리는 만들어질 수 있을 것이다.

그런데 이 경우에는 신장 트리가 될 수 없다. 왜냐하면 이 트리에서 간선 하나를 제거하고 최소 가중치 간선을 추가하면 그 트리의 가중치가 원래 트리보다 더 작아지기 때문이다.

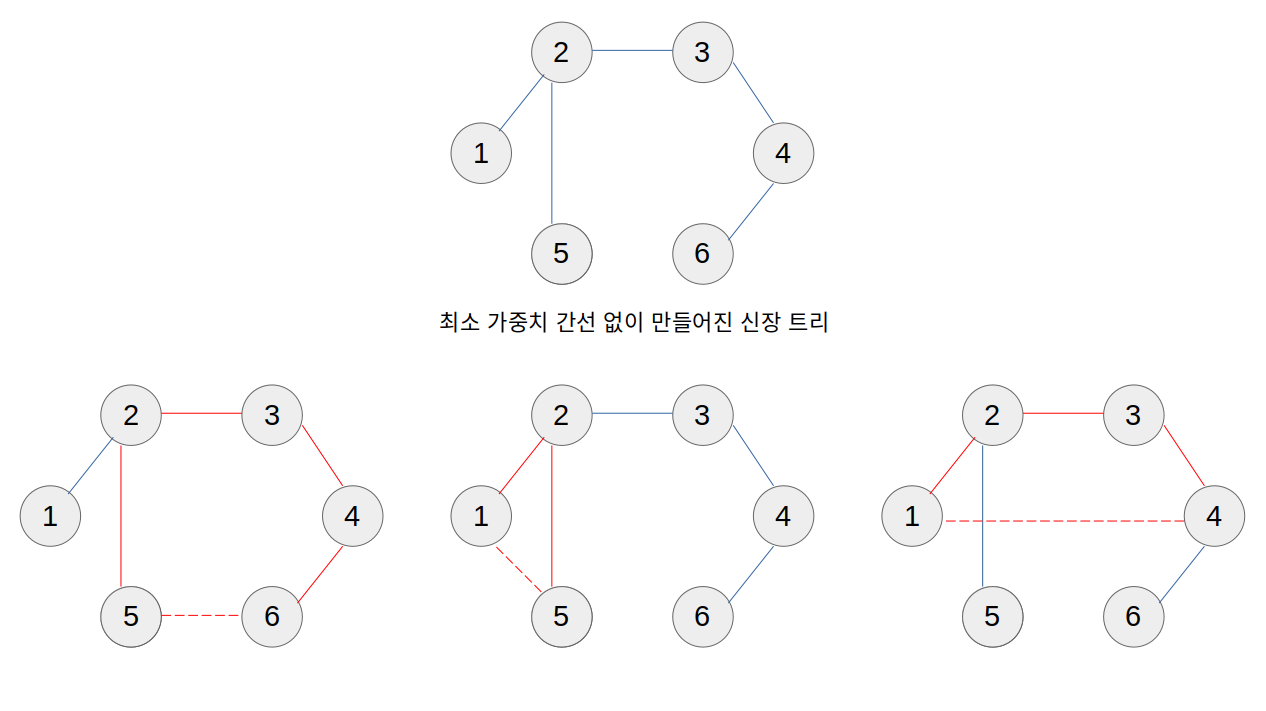
위 그림을 보자. 위의 트리는 가장 작은 가중치를 가지는 간선을 포함하지 않은 채로 만들어진 신장 트리이다.

왼쪽 아래 그림에서, 만약 최소 가중치 간선이 5-6이었다면, 2-3-4-6-5의 사이클이 만들어지게 되고, 이중 하나의 간선이 제외되어야 신장 트리가 될 수 있다.

그런데 이중 5-6을 제외한 모든 간선은 5-6보다 가중치가 작을 수 없기 때문에, 5-6 간선과 다른 간선을 교체하는 것이 가중치를 줄이는 방법이 된다.

그런데 다른 간선(5-2, 2-3, 3-4, 4-6)을 교체한다고 해서 신장 트리의 구조가 깨지지도 않는다. 5-6 간선을 추가한 뒤, 2-3-4-6-5 사이클이 만들어진 뒤 3-4 간선을 없앤다고 가정해보자. 사이클 구조를 보았을 때, 3-4 간선을 없앤다고 하더라도 4→6→5→2→3 또는 3→2→5→6→4와 같이 언제나 4에서 3로, 3에서 4으로 이어질 수 있기 때문이다.

이와 같이 다른 모든 경우에서도, 최소 가중치 간선을 추가했을 때, 그 추가한 간선 때문에 만들어진 사이클을 구성하는 간선 중 하나와 최소 가중치 간선을 서로 교체하는 것이 언제나 이득이며, 간선을 교체한다고 해서 신장 트리의 구조가 깨지지도 않는다.

따라서, 최소 신장 트리는 최소 가중치 간선을 항상 포함하도록 하는 것이 최적이다. 비슷한 과정을 통해, 두 번째로 최소인 간선을 추가하는 것이 최적임을 보일 수 있고, 같은 논리를 계속해서 전개할 수 있다. 그러므로 크루스칼 알고리즘의 결과는 항상 최소 신장 트리가 된다.

구현 (python)

def find(x):
    while x != link[x]:
        x = link[x]
    return x

def union(a, b):
		a = find(a)
		b = find(b)
		if a != b:
				link[b] = a

# edges: [source node, destination node, weight]
edges.sort(key=lambda x: x[2])
result = 0
for a, b, weight in edges:
	if find(a) == find(b):
		continue
	union(a, b)
    distance += weight

print(result)

union 연산을 V-1번 반복한 후에는 무조건 MST가 만들어져 있으므로, 조기 종료시켜도 된다.
```
count = 0
for a, b, value in edges:
		...
		count += 1
		if count >= V-1:
				break
```
두 집합을 합칠 때 원소가 더 적은 집합의 대푯값을 많은 집합의 대푯값으로 연결하는 방법을 사용할 수 있다. 이렇게 하면, 모든 경로의 길이가 $O(\log V)$ 가 되어 원소의 대푯값을 구하기 위해 경로를 따라가는 과정을 효율적으로 수행할 수 있다.
```
def union(a, b):
		a = find(a)
		b = find(b)
		if size[a] < size[b]:
			a, b = b, a
		size[a] += size[b]
		link[b] = a
```
find()를 구현할 때 경로 압축(path compression)을 활용해 경로 상의 모든 원소가 대푯값을 바로 가리키게 할 수 있다. 경로 압축이 적용되었다면, 상수 시간에 가까운 매우 빠른 시간에 find() 연산을 수행할 수 있다.
```
def find(x):
    if x == link[x]:
				return x
		result = link[x] = find(link[x])
		return result
```

시간 복잡도

작은 가중치를 가지는 간선부터 차례대로 간선을 추가해나가기 위해, 간선을 가중치가 작은 순서대로 정렬해야 하고, 이때 $O(E \log E)$ 시간이 필요하다.

이미 간선 리스트가 정렬되었다고 가정하더라도, 간선을 추가했을 때 사이클이 생겨나는지 확인하는 과정에서 $O(E \log V)$ 의 시간이 걸린다. 사이클이 생겨났는지 확인하기 위해 사용되는 union-find 알고리즘의 union과 find가 모두 $O(\log V)$ 시간에 동작하는데, 이를 간선의 개수 E만큼 반복해야 하기 때문이다.

프림 알고리즘

프림 알고리즘은 노드 선택을 기반으로 하는 알고리즘이다.

노드를 하나씩 선택해나가며 최소 신장 트리를 만든다.

프림 알고리즘은 다익스트라 알고리즘과 유사하다. 둘의 차이점은, 다익스트라 알고리즘은 시작 노드와의 거리가 최소인 노드를 구하지만, 프림 알고리즘에서는 가중치가 최소인 간선으로 연결되는 노드를 구한다는 점이다.

프림 알고리즘의 작동 방식을 세줄 요약하면 다음과 같다.

아무 것도 없는 환경에, 임의의 노드를 추가한다.
트리를 연결하는 노드 중, 가중치가 가장 작은 간선으로 연결된 노드를 선택한다.
이때, 사이클이 형성되지 않도록 한다. 이때문에 현재 선택할 노드는 이전에 선택되지 않았던 노드여야 한다.

예시

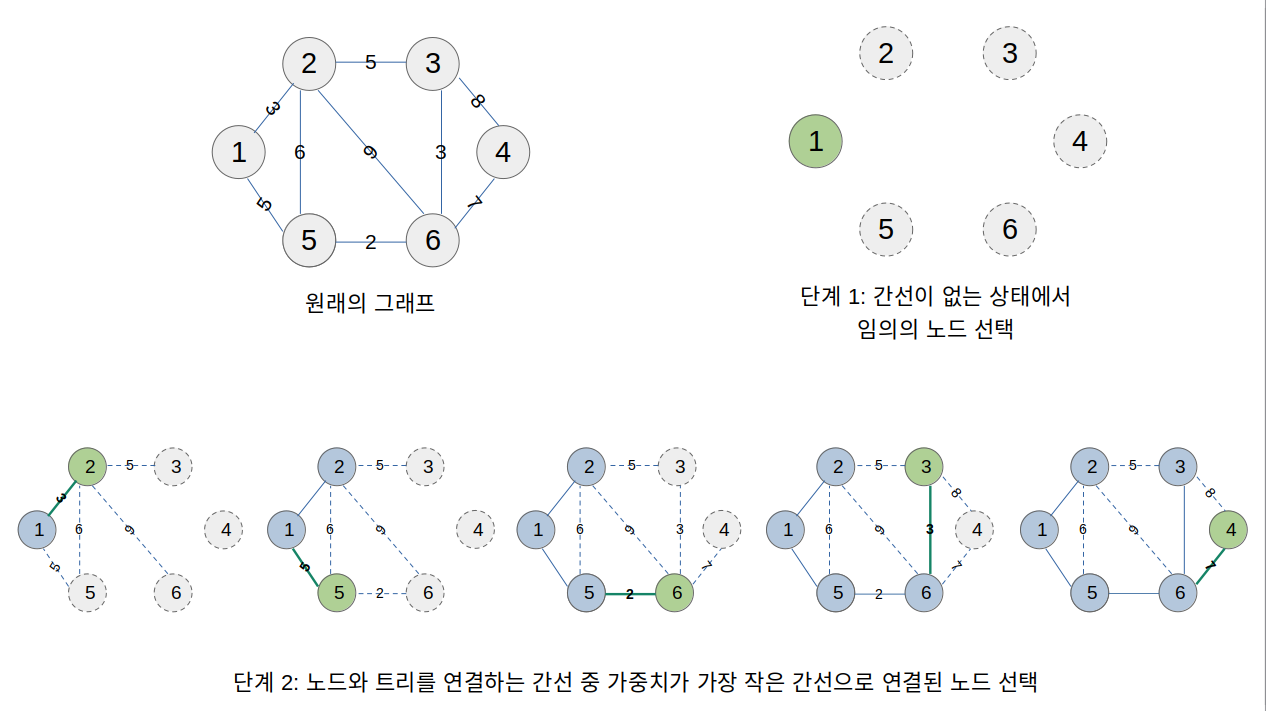
예시 그림에 대한 설명

간선이 없는 상태에서, 임의의 노드를 선택한다. 예시에서는 1번 노드를 선택했다.

노드와 트리를 연결하는 간선 중 가중치가 가장 작은 간선으로 연결된 노드를 선택해, 트리에 포함된 노드를 하나씩 늘려나간다.

트리와 연결되는 간선 중, 간선 1-2(가중치 3)이 가장 작은 가중치를 가졌으므로, 이를 이용해 2번 노드를 연결한다.

트리와 연결되는 간선 중, 간선 1-5(가중치 5)이 가장 작은 가중치를 가졌으므로, 이를 이용해 5번 노드를 연결한다.

트리와 연결되는 간선 중, 간선 5-6(가중치 2)이 가장 작은 가중치를 가졌으므로, 이를 이용해 6번 노드를 연결한다.

트리와 연결되는 간선 중, 간선 3-6(가중치 3)이 가장 작은 가중치를 가졌으므로, 이를 이용해 3번 노드를 연결한다.

트리와 연결되는 간선 중, 간선 2-5(가중치 6)이 가장 작은 가중치를 가졌으나, 간선 2-5를 연결하면 1-2-5의 사이클이 생기게 된다. 따라서 간선 2-5를 무시하고, 그 다음으로 작은 가중치를 가진 간선 4-6(가중치 7)을 이용해 4번 노드를 연결한다. 모든 노드가 연결되어 MST가 만들어졌으니 알고리즘을 종료한다.

구현

visited[start_node] = True
candidates = graph[start_node]
heapq.heapify(candidates)
result = 0

while candidates:
    weight, src, dest = heapq.heappop(candidate)
    if not visited[dest]:
        visited[dest] = True
        result += weight

        for s, d, w in graph[dest]:
            if visited[d]:
				continue
			visited[d] = True
            heapq.heappush(candidate, (w, s, d))

print(result)