문제
문제접근
문제 이해
- 겉넓이는 도형을 상, 하, 좌, 우, 위, 아래 6방향으로 바라봤을 때 단면적의 넓이를 더하면 쉽게 구할 수 있습니다.
- 하지만, 위 방법으로는 답을 구할 수 없는 경우가 있습니다.
반례
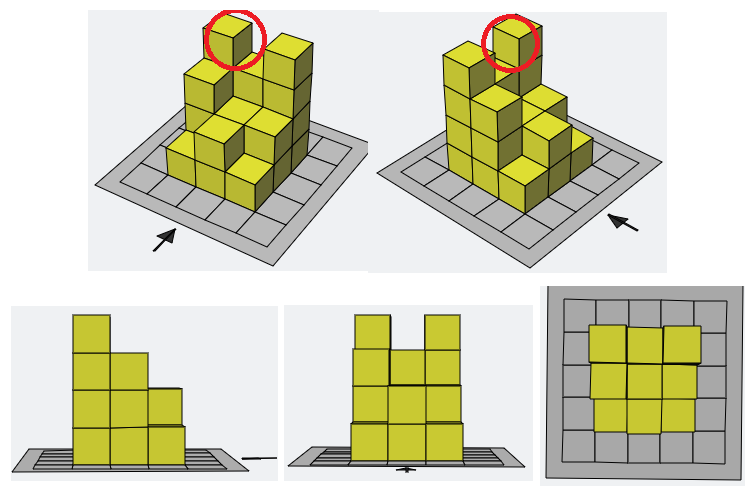
- 첫 번째 그림은 문제의 예제와 똑같이 쌓기나무를 쌓았을 때의 모습입니다.
- 두 번째 그림은 쌓기나무를 왼쪽, 앞쪽, 위쪽에서 바라봤을 때의 모습입니다.
- 왼쪽으로 본 모습은 오른쪽과,
앞쪽에서 본 모습은 뒤쪽과,
위쪽에서 본 모습은 아래쪽에서 본 모습과 같습니다.
- 따라서 답은 2×(9+11+9)=58이라고 생각할 수 있으나 답은 60입니다.
- 위 방법으로는 첫 번째 그림에서 빨간원으로 표시한 부분을 카운팅할 수 없습니다.
해결방법
- 문제를 해결하는 가장 좋은 방법은 임의의 쌓기나무에서 인접한 다른 칸과의 높이차를 계산하는 것입니다.
- 이때 쌓기나무 주위로 높이가 0인 빈칸을 반드시 만들어야 임의의 칸의 높이를 구할 수 있습니다.
- 임의의 쌓기나무 칸으로부터 인접한 4방향 칸을 조사합니다.
- 만일 인접한 칸과 높이차를 계산했을 때 양수라면 높이차만큼 답에 더해줍니다.
- 높이차가 양수라는 의미는 그 면이 바깥에서 드러나있다는 의미기 때문입니다.
- 이 방법을 사용하면 위 그림의 빨간원 표시된 부분도 5칸−4칸=1칸 으로 카운팅할 수 있습니다.
코드
#include <cstdio>
constexpr int d[4][2] = {{-1, 0}, {0, 1}, {0, -1}, {1, 0}};
int N, M, a[102][102];
int main() {
scanf("%d %d", &N, &M);
for (int y = 1; y <= N; ++y)
for (int x = 1; x <= M; ++x)
scanf("%d", &a[y][x]);
int ans = 2 * N * M;
for (int y = 1; y <= N; ++y)
for (int x = 1; x <= M; ++x)
for (int i = 0; i < 4; ++i) {
int ny = y + d[i][0], nx = x + d[i][1];
int diff = a[y][x] - a[ny][nx];
if (diff >= 0) ans += diff;
}
printf("%d", ans);
}
결과




