알고리즘 :: 백준 :: DP :: 2133:: 타일 채우기

문제

문제 링크
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.

문제접근

• 2xN 타일링의 심화버전, 그러나 접근 방법은 다르지 않다.
  • 길이가 N일 때 문제를 푸는 방법과 N-1일 때 푸는 방법이 동일하므로 최적 부분 문제 구조를 만족한다.
  • 부분 문제들이 반복해서 풀게 되므로 (i.e. N일 때, N-1일 때 모두 N-2 결과를 다시 풀게 됨) 반복구조를 만족한다.
  • 경우의 수를 구하는 문제이므로 이 문제는 DP를 사용해서 풀 수 있다고 판단할 수 있다.
• N = 6까지는 손으로 그려볼 수 있기 때문에 직접 그려보며 접근한다.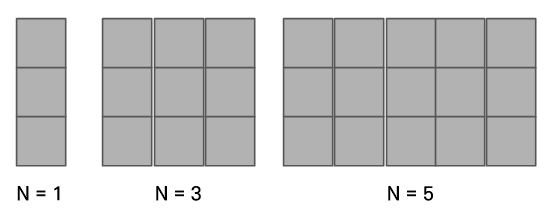
  • 
  • N이 홀수일 때는 1x2, 2x1 타일로 벽을 채울 수 없음을 알 수 있다. 따라서 입력 N이 홀수일 때는 예외처리가 필요하다.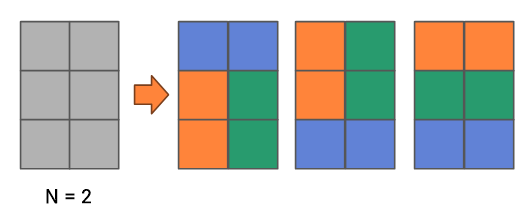
  • 
  • N = 2일 때는 다음과 같은 3가지 배치가 가능하다. N이 짝수만 허용한다면 N = 4부터는 독립적으로 3가지 씩 경우의 수가 추가될 것이므로 3 x 3 = 9가지 경우가 가능함을 알 수 있다.
  • 단순히 3을 곱해주는 것으로 문제가 끝난다면 실버1 문제가 아니다. N = 4일 때는 이런 배치도 가능하다.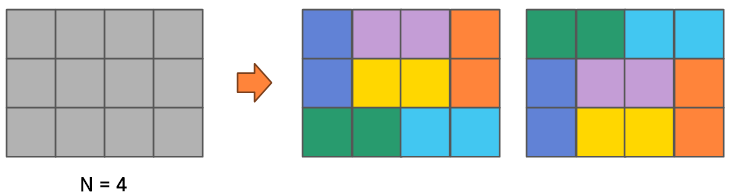
  • 
  • 경계선 상에 걸쳐서 타일이 배치되는 경우가 가능하기 때문에 N=4부터는 추가로 고려해줘야 하는 사항이 있다.
  • N=6일 때는 어떨까?
    우선 N=4일 때와 독립적으로 배치 가능한 3가지 경우가 있다.
    그리고 경계선 상에 걸쳐서 타일이 배치되는 경우가 2가지 씩 추가된다.
  • 결과적으로 다음과 같은 점화식이 나온다.
  • $D(n) = 3\times D(n-2) + 2\times (D(n-4) + D(n -6 + ...D(0))$

코드

#include <iostream>
using namespace std;
int n, dp[31];
int main() {
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n;
	dp[0] = 1;
	for (int i = 2; i <= n; i += 2) {
		dp[i] = 3 * dp[i - 2];
		for (int j = 4; j <= i; j += 2)
			dp[i] += 2 * dp[i - j];
	}
	cout << dp[n] << '\n';
}

결과