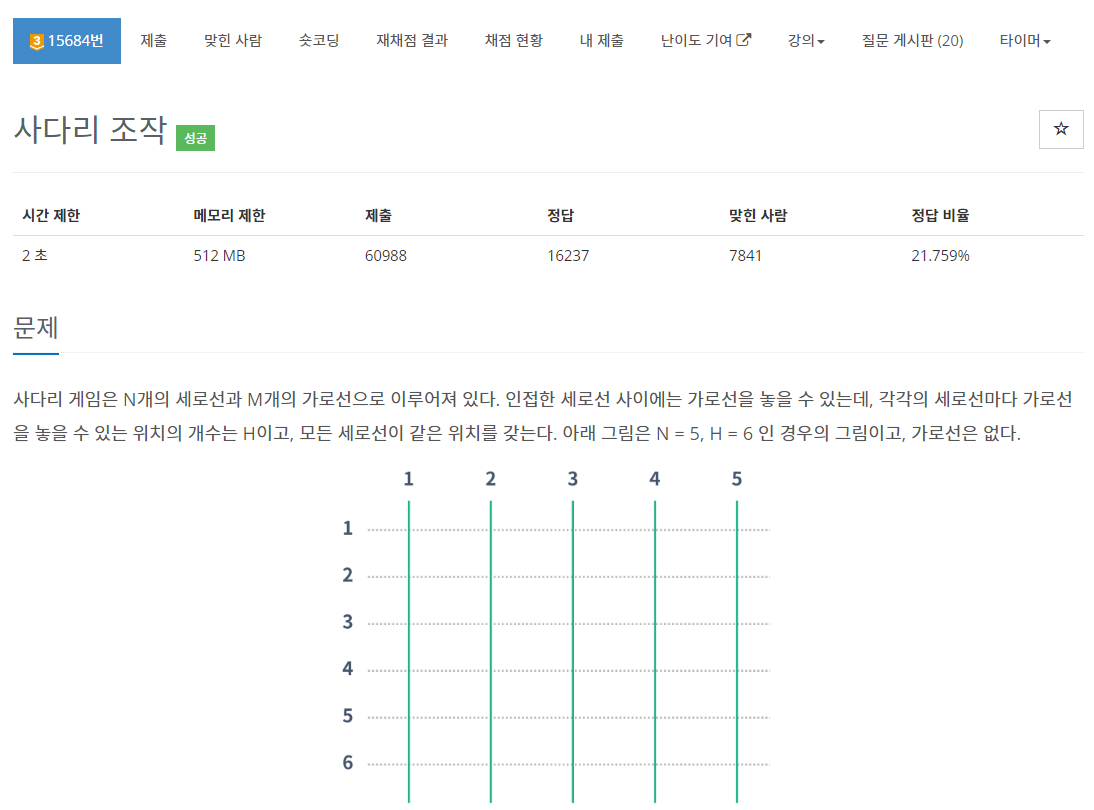
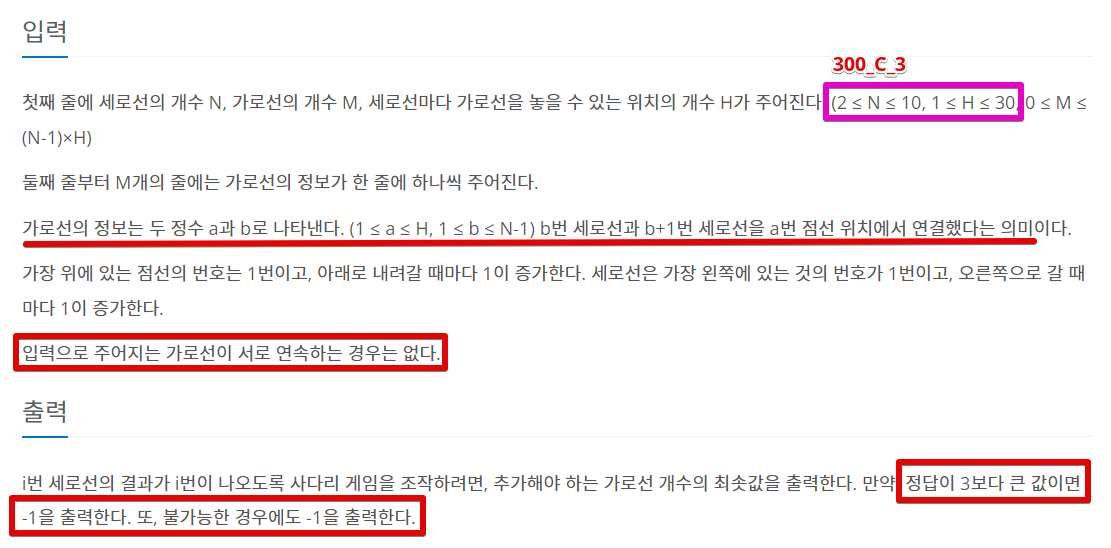
문제

문제 링크

해설

• 만일 문제조건 중 '정답이 3보다 큰 값이면 -1을 출력한다'는 조건이 없었더라면, 완전탐색으로 풀 수 없는 문제였겠지만, 다행히 추가할 가로선이 3개보다 많을 때는 더 검사하지 않아도 되므로 최악의 경우 $_{300}C_3$ 으로 약 891만 개만 탐색하면 되기 때문에 완전탐색으로 풀 수 있습니다.
• 가로선을 그었는지 여부를 저장할 bool 타입의 2차원 배열 visited[31][31] 를 선언합니다.
  • visited[y][x]가 true라면, x번째 세로선과 x + 1번째 세로선을 잇는 가로선이 y행에 그어졌다는 의미입니다.
  • 문제에서 명시한 조건을 그대로 따르는 것이 햇갈릴 가능성을 낮출 수 있습니다.
• 완전탐색을 할 것이므로 DFS 기반으로 【 표시 - 진행 - 해제 】 로직을 그대로 따를 것입니다.
• 단, 4번째 가로선부터는 검사할 필요가 없으며, 현재까지 구한 값보다 많은 가로선을 긋는 경우도 더이상 탐색할 필요가 없습니다. 따라서 백트래킹 문제이기도 합니다.
• is_arrived() 라는 함수를 만들었는데, 문제에서 요구하는 조건인 i번 세로선의 결과가 i번인지 여부를 판단하는 함수입니다.
  • 이번에 그은 가로선 덕분에 모든 세로선에서 위 조건을 만족한다면, 정답을 기록 또는 갱신합니다.

코드

#include <iostream>
using namespace std;

int N, M, H, answer = 1e9;
bool visited[31][31];

bool is_arrived()
{
	for (int x = 1; x <= N; ++x) {
		int current_pos = x;
		for (int y = 1; y <= H; ++y) {
			if (visited[y][current_pos]) current_pos++;	// 오른쪽으로 갈 수 있는 가로선 있는 경우
			else if (visited[y][current_pos - 1]) current_pos--;	// 왼쪽으로 갈 수 있는 가로선 있는 경우
		}
		// x번째에서 출발해서 x번째에 도착 못하는 경우
		if (current_pos != x) return false;
	}
	// x번째에서 출발해서 x번째에 도착하는 경우
	return true;
}

void solve(int height, int cnt)
{
	if (cnt > 3 || cnt >= answer) return;	// 백트래킹 (3 또는 현재까지 구한 답보다 크면 더 진행할 필요없음.)
	if (is_arrived()) { answer = min(answer, cnt); return; }
	for (int y = height; y <= H; y++) {
		for (int x = 1; x <= N; x++) {
			// 가로선은 연속해서 존재할 수 없다.
			if (visited[y][x] || visited[y][x - 1] || visited[y][x + 1]) continue;
			visited[y][x] = true;	// 가로선 긋고
			solve(y, cnt + 1);		// 그었다는 가정하에 더 진행
			visited[y][x] = false;	// 가로선 해제
		}
	}
}

int main()
{
	ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
	cin >> N >> M >> H;
	for (int i = 0; i < M; i++) {
		int row, col;
		cin >> row >> col;
		visited[row][col] = true;
	}
	solve(1, 0);
	cout << ((answer == 1e9) ? -1 : answer) << '\n';
	return 0;
}

소스코드 링크

결과