알고리즘::인프런::큰돌

문제링크ROT13은 대문자/소문자 영문자를 13글자 앞 또는 뒤로 밀어서 만든 만든 새로운 문자열을 의미합니다.13번째 알파벳인 'M'을 기준으로 13을 더하면 'Z'이므로, 14번째 알파벳인 'N'은 13을 더하면 안 되고 'A'로 돌아가야 합니다.그러므로, 14번째

문제링크별문자(\*)를 기준으로 앞쪽 문자열(prefix)와 뒤쪽 문자열(suffix)을 추출합니다.주어진 문자열의 앞쪽부터 검사하며 prefix를 포함하는지 검사합니다.주어진 문자열의 뒤쪽부터 검사하며 suffix를 포함하는지 검사합니다.이때, 주어진 문자열은 pre

문제링크문자열을 입력받았을 때 정수를 반환하기 위해 key-value 구조로 데이터를 저장하는 map STL 컨테이너를 떠올리면 성공입니다.하지만, 정수(value)를 입력받았을 때 문자열(key)을 반환하는 방법이 없습니다.따라서, 공간복잡도 O(n)을 더 소모하지만

문제링크아이디어 하나가 떠오르지 않으면 한참을 해매는 전형적인 문제입니다.예제입력의 첫 번째 테스트 케이스를 기준으로 설명해보겠습니다옷 종류는 headgear와 eyewear 두 가지 종류가 있고, headgear은 2가지, eyewear은 1가지 옷이 있습니다.옷의

문제링크우선 팰린드롬이 ‘절대 만들어질 수 없는 조건’을 파악합니다.홀수번 등장하는 알파벳이 2개 이상이면 팰린드롬을 만들 수 없습니다.팰린드롬의 구조는 다음 두 가지 중 하나입니다.홀수번 등장한 알파벳이 0개: (prefix) + (뒤집힌 prefix)홀수번 등장한

문제링크A^B를 C로 나눈 나머지를 구해야 하는데, A, B, C 모두 범위가 약 21억입니다.O(log(N))으로 풀지 않으면 100% 시간초과에 걸리며, 중간과정에 int 범위를 넘기 때문에 A, B, C는 unsigned long long 자료형으로 선언해야 합니

문제링크어렵게 생각하면 한없이 어려워질 수 있는 문제입니다.우선 1, 11, 111 … 을 만드는 방법은 1부터 시작해서 10을 곱한 뒤 1을 더하면 됩니다.이 문제의 최대 난관은 ‘어떻게 자료형 오버플로우를 막을 것인가’입니다.주어지는 수는 2와 5의 배수가 아니기

문제 [문제링크](https://www.acmicpc.net/problem/2468 해설 코드 소스코드 링크 결과

문제링크두 가지를 조심하면 되는 문제입니다.분할할 필요가 없는 경우 괄호 ‘()’를 삽입하지 않습니다.더 이상 분할할 수 없는 경우에 대한 예외처리를 반드시 고려해야 합니다.우선, 분할할 필요가 있는지 없는지 여부를 검사해야 합니다. 범위 내에 단 하나라도 다른 요소가

문제링크실버4 난이도 답지않게 신경쓸 사항이나 반례가 은근히 많은 문제입니다.0이 앞에 나올 경우, 0을 생략하거나 제거하는 절차가 필요합니다.00이나 000같은 0으로만 이루어진 숫자는 0으로 취급해야 합니다.문장 끝에 숫자가 있을 때도 적절한 처리가 필요합니다.문장

문제 링크이런 종류의 문제는 항상 ‘정확히 해당 숫자’를 구할 필요가 없고, 오버플로 때문에 시간 내에 구할 수도 없습니다.대략 10!를 직접 손으로 해보면 어떻게 풀 수 있을지 감이 잡힙니다.1, 2, 3, 4 팩토리얼은 0이 없습니다.5! = 5 × 4 × 3 ×

문제 링크함정문제입니다.0666, 1666, 2666, 3666, 4666, 5666,6660, 6661, …., 6669, 7666, 8666, 9666총 19개… 그게 10666부터 11666까지…이렇게 빠져들기 시작하면 이 문제의 함정에 빠진 것입니다 ㅎㅎ함정에

문제 링크연구실의 크기는 최대 8×8이고, 놓을 수 있는 벽의 개수가 3개이므로최악의 경우, 바이러스가 연구실에 벽이 하나도 없고, 바이러스가 딱 2곳 있다면3개의 벽을 세울 수 있는 경우는 62 x 61 x 60이고각 경우의 수마다 DFS로 바이러스를 전파하고, 안전

문제 링크시뮬레이션(구현) 문제 + DFS/BFS 문제이므로 문제에서 요구하는대로 시키는대로 그대로 구현하면 됩니다.치즈가 남아있는 동안 while() 루프를 돌면서시간(answer_time)을 증가하고공기에 닿은 치즈 겉표면을 (아직 제거하진 않고) 표시만 하는 me

문제 링크항상 머릿속에 ‘트리도 그래프의 한 종류다’ 라고 넣어두면 좋습니다.우선 루트노드의 부모도의 번호가 -1이고, 인덱스 번호가 음수인건 좋지 않으므로 입력받는 모든 부모노드에 1을 더해 입력받았습니다.따라서 루트노드는 1번노드이며, 0번노드라는 눈에보이지 않는

문제 링크‘트리도 그래프의 일종이다’ 라는 개념을 머릿속에 꼭 넣어둡시다.따라서 트리를 연결리스트로 취급해서 DFS로 리프노드를 찾아내면 쉽게 풀 수 있습니다.이 문제에서 숨겨져있는 함정은 사이클이 존재할 수도 있다는 점입니다.예를 들어 A가 B를 신뢰하고, B가 A

문제 링크N이 100만이므로 O(N²)으로 절대 풀 수 없고 최소한 O(N×logN)으로 풀어야 합니다.arr5 = 3 8 2 7 9 이라는 예를 생각해봅시다.처음에는 ans 배열을 -1 -1 -1 -1 -1 로 초기화합니다.뒤에서부터 생각해봅시다. 9는 당연히 맨 끝

문제 링크두 가지 방법으로 풀 수 있습니다.조합( 헤더파일의 next_permutation() 함수)을 이용하는 방법재귀함수를 이용하는 방법입력받은 데이터 중 치킨집의 개수를 chicken_cnt 라는 변수로 카운팅합니다.chicken_cnt 크기의 bool 타입 배열

문제 링크보물의 위치가 주어지고, 시작 위치에서 보물까지 최단거리를 구하는 일반적인 문제와 달리 이 문제는 시작위치와 도착위치가 정해져있지 않습니다.그러므로 임의의 육지 상 좌표에 대해 BFS를 수행해 갈 수 있는 모든 좌표의 최단거리를 구하고 그 중 가장 긴 거리를

문제 링크인구 이동을 하려면 어떤 정보들이 필요할까요?국경을 개방한 국가의 좌표가 필요합니다.그래야 좌표들을 토대로 인구의 합과 평균을 구할 수 있기 때문입니다.따라서, 임의의 좌표 (y, x)에서 DFS를 수행할 때, 국경을 개방할 조건 (L <= 인구 차이 &

문제 링크코딩테스트 문제풀이에서 가장 까다로운 점 중 하나는 ‘동시성’ 구현입니다.예를 들어, 이 문제에서는 지훈이와 불이 같은 시간에 움직여야 합니다.하지만, 그 어떤 언어로도 코딩테스트에서는 ‘동시성’을 쉽게 구현할 수 없습니다.또한, ‘동시성’을 구현하도록 묻는

문제 링크쉬운듯 보이면서도 막상 풀기 시작하면 고려할게 참 많은 문제입니다.중간에 사망하는 몬스터가 생기면 몬스터 수가 줄어들고몬스터 수가 바뀌면 고려해야 하는 데미지 조합과 조합 개수가 바뀌며무엇보다 체력이 최대 60밖에 안 되지만, 최악의 경우에 호출되는 콜스택 횟

문제 링크이 문제가 대표적인 ‘조합’으로 풀려고 할 때 함정에 빠지는 문제입니다.아마 조합으로 풀려고 하셨던 분들께서는, 각 연산자에 번호를 할당하고 괄호가 0개, 1개, 2개, … , ceil(N / 2)개 인 경우에 대해 조합을 구하려고 하셨을 것 같습니다.그리고

문제 링크수빈이가 이동할 수 있는 경우의 수는 좌표 x를 기준으로 {x - 1 , x + 1, x \* 2} 3가지 입니다.또한, 동생을 찾기 위한 최단거리를 찾아야 하므로 BFS를 사용해야 함을 알 수 있습니다.즉, 일반적으로 2차원 배열 상에서 이뤄지던 DFS/BF

문제 링크이 문제는 다른 포스트에서 이미 다룬 적이 있기 때문에 해당 포스트 주소를 올리는 것으로 대체하겠습니다.소스코드 링크

문제 링크동생의 위치가 매 초마다 정방향으로 움직인다는 특수성 때문에 고려해야할 새로운 경우의 수가 생깁니다.바로 가만히 있는게 빠를 수도 있다는 것입니다.예를 들어, 예제 입력 2의 17 5의 경우수빈이가 17 -> 16 -> 15 -> 16 -> 15로 좌표 16,

문제 링크문제 설명이 조금 애매해서 이해하는게 조금 어려울 수 있습니다.주난이가 한 번 점프하면 파동은 4방향으로 친구를 맞을 때까지 주욱 전진하는 겁니다.위와 같이 주난이가 점프한 뒤 \- 한 칸 뒤가 '0'이라면, 그 칸으로부터 다시 4방향으로 파동이 퍼져나갑니

문제 링크【얼음을 녹인다 -> 백조가 만나는지 확인한다 -> 못 만났다면 반복한다.】 로직을 반복하면 풀 수 있습니다.첫 장애물은 동시성 입니다. '얼음'을 기준으로 얼음을 녹일 시 방금 녹은 얼음이 지금 녹을 예정인 얼음에 영향을 줄 수 있기 때문에 이 문제는 '물'

문제 링크아주 전형적으로 DFS 재귀로도 풀 수 있고, 최적값을 찾는 문제이기도 하므로 BFS로도 풀 수 있는 문제입니다. (미리 말씀드리지만, DFS가 훨씬 빠르게 풀 수 있는 문제입니다.)같은 알파벳이 적힌 칸을 두 번 지날 수 없기 때문에 26개의 알파벳을 각각

문제 링크i - 1번쨰 칸에 고른 숫자와 i - 1번째 부등호가 성립하는 i번쨰 숫자를 고르며 모든 경우의 수를 탐색하는 것이 이 문제의 핵심이었습니다.선택된 숫자는 모두 달라야 한다는 조건이 있기 때문에, visited\[10] 이라는 bool 타입 배열을 만들 수도

문제 링크어렵지 않게 in-order 방식으로 입력이 주어지는 문제임을 알 수 있습니다.이 문제는 두 가지 접근법으로 풀 수 있습니다.먼저 완전이진트리 성질을 이용해서 푸는 방법입니다.문제에서 주어지는 in-order 방식의 입력을 level 별로 출력하기 위해서는!\

문제 링크단순 구현 문제입니다.화단은 최대 10×10이고 씨앗은 총 3개이므로 충분히 bruteforce로 검사할 수 있습니다.꽃은 4방향으로 피기 때문에 좌표는 (1, 1)부터 (N - 2, N - 2)까지만 검사하면 범위를 넘어가서 죽는 꽃을 굳이 검사하지 않아도

문제 링크좌표 (R-1, 0)에서 (0, C-1)로 cnt번 이동해서 가는 경우의 수를 구하는 문제입니다.DFS를 이용하면 쉽고 깔끔하게 풀 수 있습니다.소스코드 링크

문제 링크만일 문제조건 중 '정답이 3보다 큰 값이면 -1을 출력한다'는 조건이 없었더라면, 완전탐색으로 풀 수 없는 문제였겠지만, 다행히 추가할 가로선이 3개보다 많을 때는 더 검사하지 않아도 되므로 최악의 경우 $\_{300}C_3$ 으로 약 891만 개만 탐색하면

문제 링크주어진 최대 15가지의 식재료 중 조건을 만족하는 최소 가격 조합을 찾아야 하므로 모든 경우의 수를 탐색해야 합니다. 따라서 모든 경우의 수는 2¹⁵로 시간제한 내로 풀 수 있습니다.특히 '15가지'라는 점에 주목합시다. 32 이하의 수일 때 한 번쯤 '비트

문제 링크굉장히 어려운 문제였습니다. 행과 열에 대해 각각 2²⁰가지 조합을 어떻게 시간초과 없이 해낼 것인지 도무지 감을 잡기 어렵기 때문입니다. 문제를 풀기 위해서는 세 가지 아이디어가 필요합니다.앞면(H)/뒷면(T) 두 가지 상태가 있다는 점에서 이진법(bool)

문제 링크어떤 노드(선거구) A와 B가 서로 연결돼있는지 확인하기 위해서는 DFS 또는 BFS를 사용해야 합니다.노드는 총 10개고 두 그룹으로 나누는 경우의 수는 2^10가지로 충분히 시간내에 풀 수 있습니다.우선, N개의 노드를 두 그룹으로 나눈 뒤각 그룹이 적어도

문제 링크알파벳은 비트마스킹과 궁합이 정말 좋습니다.알파벳은 26개라 2²⁶(67,108,864)로 int형 변수 1개의 0번부터 25번 bit을 조작해 표현할 수 있습니다.이 문제는 중복 알파벳 칸을 지나갈 수 없기 때문에 지나간 알파벳을 기억하고 있어야 합니다.DF

문제 링크 조건이 많아서 까다로운 문제입니다. 최대한 자신만의 언어로 조건을 단순화 하는 것이 중요합니다.저는 이렇게 단순화했습니다." 길이 L, 높이 1 경사로를 평탄한 면 위에 중복없이 놓아서 지나갈 수 있는 길 카운트"이제 세부조건은 다음과 같습니다. 가로 길에

문제 링크비트마스킹이 익숙하지 않다면, 아이디어가 떠오르지 않아 정말 어려울 문제입니다.최대 크기가 4×4 밖에 안 되지만, 임의의 좌표 (y, x)에서 최대 15가지 경우의 수가 만들어집니다.물론 (y+1, x), (y, x+1)로 갈수록 만들어질 수 있는 경우의 수

문제 링크트리는 그래프의 일종임을 바탕으로 주어진 입력이 그래프인지, 트리인지 식별하는 문제입니다.문제에서는 '연결성' + '간선이 1개만 연결됨' + '간선 추가하면 사이클 생성됨' 세 가지 구분법을 제공합니다.'트리의 모든 노드는 연결돼있다'라는 정보와 '트리의 모

문제 링크이 문제는 시간 내 풀이하는 조건이 가장 까다로운 문제입니다.문제 마지막 조건 ('전체 T에 주어지는 p + n <= 70만')에 따라 반드시 O(n) ~ O(nlog(n))에 풀어야 합니다.함수 R(뒤집기)이 이 문제의 함정입니다.STL <algo

문제 링크브론즈급 쉬운 문제지만, 재밌는 반례 때문에 개인적으로 골머리를 앓았던 문제였습니다 ㅎㅎㅎ."pi", "ka", "chu" 세 문자열을 주어진 문자열 속에서 찾아 (find()) 해당 문자열이 세 부분 문자열로만 이뤄져있는지 검증하면 됩니다.이때, find()

문제 링크까다로운 문제입니다.(()(()과 (()()) 는 한 글자 차이인데 답은 2와 6으로 차이가 납니다.위 반례를 근거로 단순히 (, ) 문자로 스택에 push(), pop() 하는 방법으로는 어떤 (를 만났을 때 이후 ) 존재할 지 여부를 알 수 없다는 것을 알

문제 링크N이 최대 50만이므로 O(N)~O(NlogN)에 풀어야 하는 어려운 문제였습니다.위와 같이 사람이 서 있을 수 있는 경우의 수는 4가지 입니다.1, 2번처럼 오름차순/ 내림차순으로 서있는 경우, 절대로 자기 옆사람 이외에는 다른 사람을 볼 수 없기 때문에 N

문제 링크DFS + 비트마스킹 + 구현 문제입니다.요구조건 1, 2번은 전형적인 connected component 찾기 문제입니다.(0, 0)부터 (N - 1, M - 1)까지 visited\[]\[] 배열을 잘 사용하면서 DFS를 사용해 연결된 요소가 몇 개인지,

문제에 접근하는 순서는 무조건 Bruteforce ▶ DP ▶ Greedy 순서입니다.Greedy(그리디) 알고리즘을 적용하기 위해서는 부분 문제의 최적해가 전체 문제의 최적해가 됨을 증명해야 합니다.코딩테스트의 시간제약 특성 상 시험시간 내에 이를 증명하는 것은 불가

문제 링크N일 내로 최대로 돈을 벌기 위해서는 n일에 선택할 수 있는 강의 중 최대한 이득이 되는 강의를 선택해야 합니다.1일차에 선택할 수 있는 강의들 중 가장 보수가 쌘 것을 일단 선택합니다.2일차에 선택할 수 있는 강의들 중 가장 보수가 쌘 것을 선택합니다.이때,

문제 링크문자열의 길이가 최대 100만입니다. 따라서 2중 for문을 사용한 bruteforce O(n²) 알고리즘을 사용하면 시간초과가 납니다.문제 풀이의 핵심은 폭발문자열을 만났을 때, 연쇄폭발을 효과적으로 처리하는 것입니다.예를 들어, 폭발문자열이 C4일 때, C

문제 링크이 링크에서 설명했듯, 그리디 문제는 sort() 후 priority_queue<>에 조건에 맞게 삽입해서 문제를 해결합니다.그러므로 위 링크의 문제와 해결 코드가 상당히 비슷한 것을 확인할 수 있습니다.모든 문제는 푸는 데 1일이 소요되는 점 ↔ 모든

문제 링크소의 도착시간과 검사시간을 하나의 선으로 나타내면 위와 같습니다.먼저 소의 도착시간에 따라 오름차순으로 정렬하면 위 그림의 아래와 같습니다.오름차순으로 정렬한 이유는 '라인스위핑 알고리즘'을 적용하기 위해서입니다.라인스위핑은 그리디 알고리즘과 마찬가지로 최적해

문제 링크회의실을 최대한 사용하기 위해서는 더 빨리 시작하고 더 빨리 끝나는 회의를 고르는 것이 유리하다는 것을 알 수 있습니다.따라서 빨리 시작하는 것을 알기 위해서는 모든 회의를 시작시간에 대해 오름차순으로 정렬 sort() 해야 합니다.예제를 예를 들어, 이 문제

문제 링크우선 N, K의 범위가 30만이므로 적어도 O(N\*logK) 알고리즘을 사용해야 하며, 최대 무게 Ci가 1억이고, 이게 K개 있을 수 있기 때문에 답은 int 범위를 넘을 수 있다는 점을 먼저 확인합니다.우선, 보석의 무게와 가방의 용량을 오름차순으로 정

문제 링크문제를 풀기 전에 먼저 점의 위치가 음수 -10억부터 양수 10억까지 int 범위가 가능하기 때문에, 점의 위치를 나타내는 변수의 초깃값을 0으로 하는 실수에 유의합시다.당연히 20억 + 1개의 점이 존재할 수 있기 때문에 수직선을 의미하는 배열은 만들 수 없

문제 링크수열의 길이는 최대 10만이므로 연속해서 합산할 범위의 시작점과 끝점을 두 개의 for문을 사용해서 모든 경우의 수를 구하는 O(n²) 알고리즘이 가장 간단하지만, 시간 내애 풀 수 없습니다.N개의 수열을 입력받으면서 특정 조건을 적용해 최적해를 빠르게 구하는

문제 링크우선 소수를 빠르게 판별하는 알고리즘으로는 '에라토스테네스의 체'가 있습니다.에라토스테네스의 체는 O(log(N)에 N까지의 소수를 판별할 수 있기 때문에 약 3, 4줄 밖에 안 되므로 하나의 공식처럼 코드 덩어리를 외워두는 것이 좋습니다.입력되는 자연수 N이

문제 링크수열의 길이가 최대 10만이므로, (O(N²)이 소요되기 때문에) bruteforce하게 문제를 풀면 안 된다는 것을 알 수 있습니다.우선 연속해서 더할 구간의 시작점(left)과 끝점(right) 이라는 아이디어는 분명히 좋은 아이디어니까, 이 투포인터를 어

문제 링크전형적인 투포인터 문제입니다. 수열의 길이가 최대 10만이므로 O(N²)이 소요되는 bruteforce로는 풀 수 없습니다. 우선, 수열을 오름차순으로 정렬합니다. (O(NlogN))수열에서 더할 두 값을 left와 right이라는 포인터로 지정한 뒤더한 값이

문제 링크구현도 어렵지만, 구현하기 전에 문제를 풀기위한 아이디어를 떠올리는 것도 어려운 문제입니다.플러그를 빼는 횟수를 최소화하기 위해서는, 현재 꽂혀있는 플러그들 중 가장 먼 미래에 사용하거나, 아예 사용할 계획이 없는 플러그를 뽑는것이 가장 좋습니다. 이 아이디어

문제 링크일반적인 구현 문제입니다만, 골드 상급(난도 중상) 시뮬레이션 문제답게 문제에서 요구하는 구현 사항이 많습니다.문제의 요구사항들을 1, 2, 3 순서대로 하나씩 적어나가면서 전체적인 프로그램의 기틀을 만든 뒤 각 함수를 만드는 것을 추천드립니다.다행히도, 이

문제 링크어려운 구현문제답게 요구하는 작업이 많습니다. 최대 20x20에, 이동은 5번이므로 재귀함수를 사용해서 모든 경우의 수를 탐색하면 시간내에 문제를 풀 수 있을 것 같습니다.위, 아래, 오른쪽, 왼쪽 이동 연산은 위와 같이 각 경계선의 끝지점부터 시작해서 반대쪽

문제 문제 링크 해설 코드 소스코드 링크 결과

문제 링크그림이 많고 복잡해보여서 기선제압을 하는 종류의 시뮬레이션 구현 문제입니다.하지만, 당황하지 마시고, 입력받는 n번째 톱니바퀴를 기준으로 왼쪽으로는 어디까지 같이 회전하는지, 오른쪽으로는 어디까지 같이 회전하는지 구하신 뒤, 문제에서 요구하는대로 서로 반대방향

문제 링크대표적인 라인스위핑 문제 중 하나로, 이 문제(문제링크, 해설링크)와 유사합니다.웅덩이의 범위가 10억까지이므로 메모리 제한 때문에 절대 좌표상으로 나타낼 수 없습니다.따라서, 입력받은 물웅덩이를 시작점에 따라 오름차순으로 정렬한 뒤, 시작점부터 끝점까지 널빤

문제 링크어쩌면 가장 당황스러운 종류의 시뮬레이션 문제인 것 같습니다. 가장 구현에 가까운 문제일 수도 있곘네요.문제에 주어진 윷놀이 도형을 어떻게 하면 구현할 수 있을까요? 10, 20, 30이 적힌 노드에서 두갈래로 나뉘고, 해당 점에 멈췄을 때는 무조건 파란 화살

문제 문제 링크 해설 코드 소스코드 링크 결과

문제 링크(개인적으로는 Chapter 5 구현 문제들 중 가장 어려웠습니다. 이번 문제 덕분에 기하문제는 어렵게 생각하지 말고 규칙성 파악 후 단순 구현하면 되는 것이란 걸 배웠습니다.)문제의 표현 중 '드래곤 커브를 끝점을 기준으로 시계 방향으로 90도 회전시킨 다음

문제 링크( 다양한 아이디어를 적용해야 제한시간 내에 풀 수 있는 어려운 문제였습니다. )피자 A, B가 각각 최대 1,000조각 씩 있기 때문에 아쉽게도 O(N²) 방법으로는 시간 내에 풀 수가 없습니다. (1000C1 + 1000C2 + 1000C3 + ... +

문제 링크N x M은 최대 8 x 8이고 CCTV의 개수는 최대 8개이므로 모든 경우의 수를 탐색하는 전형적인 bruteforce 시뮬레이션 + 재귀(DFS) 문제입니다.다만, 조금 까다로운 점은 CCTV를 회전하는 연산이 포함돼있다는 점입니다.CCTV 종류(1, 2,

O(N) ~ O(N²)으로는 절대 시간내에 풀 수 없는 탐색범위를 조건으로 가진 문제라면 이분탐색을 한 번쯤 생각해볼 수 있습니다. (e.g. 탐색해야 하는 N의 범위가 1억 이상이라던지…)이분탐색은 (당연히) 정렬되거나 모든 값이 같은 값으로 초기화 된 배열에 대해

문제 링크질투심 = 가장 많은 보석을 가져간 학생이 가진 보석갯수최대 아이들의 수는 10억이기 때문에 이 문제는 일반적인 O(N)~O(N²) 방법으로는 시간 내에 해결할 수 없다는 것을 알 수 있습니다.따라서, 질투심이 mid일 때, N명의 학생에게 보석을 나눠줄 수

문제 링크문제가 조금 난해하게 적혀있어서 이해하기 어렵습니다. 다시 정리하면 아래와 같습니다.주어지는 N개의 강의는 순서가 바뀌어선 안됩니다. N개의 강의를 M개의 블루레이에 넣으려고 합니다. 이때, 블루레이가 얼마나 팔릴지 알 수 없기 때문에 블루레이의 크기는 최소한

문제 링크문제가 조금 너무할 정도로 이상하게 해석돼있습니다. 다시 정리해서 적으면 다음과 같습니다.현우는 용돈을 효율적으로 활용하고, 돈을 펑펑 쓰지 않기 위해서 앞으로 N일 동안 자신이 매일 사용할 금액을 계산하고, 정확히 통장에서 M번, K원 씩 출금해서 사용하기로

문제 링크방의 개수(N)와 몬스터의 체력(h)의 범위가 커서 최악의 경우에는 시간초과가 날 수 있는 구현문제입니다. 각 방에서 해야하는 일이 순서대로 정리돼있기 때문에 문제에 나와있는대로 구현만 하면 됩니다.하지만, 시간초과를 방지하기 위해 for문으로 정직하게 한 턴

문제 링크게임 횟수(X)와 이긴 게임 횟수(Y)가 10억까지 입력 가능하고, 입력값에 따라 int 범위를 충분히 넘어갈 수 있기 때문에 안전을 위해 long long 또는 unsigned long long 자료형을 사용합시다.승률 계산은 소수점을 버려야하므로 floor

문제 링크수첩1과 2가 각각 최대 길이가 100만이므로 가장 쉬운 방법인 O(N²) 방법 (각 수첩2의 요소마다 수첩1을 처음부터 끝까지 탐색하는 방법)을 사용하면 안 됩니다.std::binary_search() 함수를 연습하는 문제입니다.먼저, 이분탐색을 사용하기 앞

문제 링크문제를 요약하면, ' S개의 파를 길이 L의 파로 자를 때 C개의 덩어리를 만들 수 있는가? '' 이때 L의 최댓값을 구하고, 정답은 요소의 합 - L을 출력하시오. ' 입니다.L은 최대 10억, S는 최대 100만이기 때문에 일반적인 방법으로는 100% 시간

문제 링크어려운 문제입니다. 우선, 언듯 보기에는 차근차근 각 1분씩 진행하거나 또는 입력받은 M개의 놀이기구의 최소공배수씩 시간을 늘려가면서 N명의 아이들이 놀이기구에 탑승할 수 있도록 처리해야 할 것 같습니다.하지만, N의 범위가 최대 20억까지이며, M도 1만까지

문제 링크N이 최대 100만이므로 DP를 이용해도 O(N²) 알고리즘이기 때문에 시간초과가 납니다.LIS의 경우, std::lower_bound()를 이용하면 O(NlogN)에 길이를 구할 수 있습니다.하지만 이때, LIS의 내용물이 계속해서 overwrite되고, 원

문제 링크증가하는 부분 수열 (LIS)은 DP를 이용한 방법(O(N²))과 이분탐색을 이용한 방법 (O(NlogN))이 있지만, 감소하는 부분 수열은 DP 밖에는 방법이 없는 것 같습니다.1로 초기화된 dp 배열을 만듭니다.왜냐하면, 모두 자기자신을 부분수열로 하기 때

문제 링크문제에서 알고리즘의 psuedo code가 주어지므로 그대로 재귀호출 함수를 구현하면 됩니다.다만, a, b, c 셋 중 하나라도 0을 포함한 음수일 경우, 20을 초과한 자연수일 경우에 특수한 조건이 있습니다.입력조건을 보면 세 변수의 범위는 -50 부터

문제 링크00 또는 1 타일만 사용할 수 있는 상황입니다.DP\[N]을 N개의 타일을 놓을 수 있는 최대 경우의 수라고 정의합시다.N - 2개의 타일을 놓았을 때, 00 타일을 놓는다면, N개의 타일을 놓을 수 있습니다.N - 1개의 타일을 놓았을 때, 1 타일을 놓는

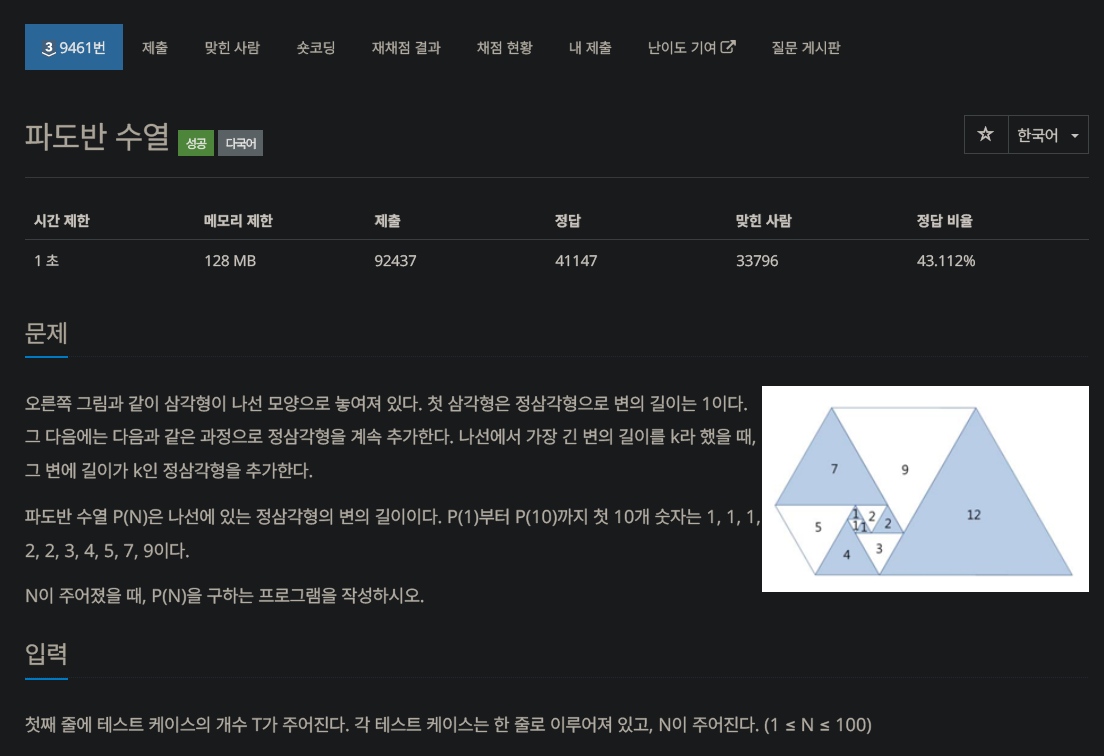
문제 링크파도반 수열의 형태를 보면, 5번째 삼각형 까지(1, 1, 1, 2, 2)는 규칙성을 찾기 어렵지만, 그 뒤부터는 반드시 다른 두 삼각형과 인접한 형태이므로 변의 길이가 증가합니다.이때, 인접하는 삼각형은 이전 두 삼각형입니다.문제에 첫 10개의 수열이 주어지

문제 링크인접한 두 집의 색상이 같아서는 안 된다는 규칙이 중요합니다.하나의 집을 세 가지 색깔로 칠할 수 있기 때문에 i번째 집에 3가지 경우의 수가 생깁니다.그러므로, DP\[i]\[0] = i번째 집을 빨간색으로 칠했을 때 최소 비용으로 정의합니다.인접한 두 집의

문제 링크\[y]\[x]는 \[y + 1]\[x]와 \[y + 1]\[x + 1] 두 요소로 타고 내려갈 수 있습니다.1층은 원소가 하나밖에 없기 때문에 항상 최댓값을 가집니다.2층부터는 위 두 요소 중 더 큰 값으로 최댓값으로 초기화하면서 한 층씩 내려가면 됩니다.소

문제 링크'시작점'이 따로 있다는 점, '도작점'을 반드시 밟아야 한다는 점은 놓치기 쉬운 조건입니다. 반드시 챙겨야 합니다.연속해서 3개의 계단을 오를 수 없습니다.즉, 어떤 i번째 계단을 올랐을 때, 연속해서 1개 오른 상태, 연속해서 2개 오른 상태, 연속해서 3

문제 링크길이가 2 이상일 때부터는 가장 앞자리에 0이 올 수 없으며,계단수가 되기 위해서는0은 무조건 1로 증가하는 방향만 고려해야 하고,9는 무조건 8로 감소하는 방향만 고려해야 합니다.그러므로, 길이가 N - 1일 때 맨 앞자리에 어떤 수가 오느냐에 따라 N일 때

문제 링크이 문제와 많이 유사한 문제입니다.다만 중요한 차이점이 있는데, 반드시 1칸 or 2칸 움직여야 한다는 제약조건이 없다는 점입니다.즉, 최적해를 위해서라면 포도주를 2개 이상 생략할 수도 있습니다.위에서 언급했듯, 가장 많은 양의 포도주를 마시는 것 == 최대

문제 링크LCS는 대표적인 DP 문제로 푸는 방법이 정해져있으니 외워두는 것이 좋습니다.공집합도 부분집합의 하나이므로, 빈문자(공백)를 포함해서 DP\[첫번째 문자열 길이 + 1]\[두번째 문자열 길이 + 1] 크기의 2차원 메모이제이션 배열을 생성합니다.빈문자는 부분

문제 링크외판원 문제는 대표적인 NP 완전 문제입니다. NP 완전 문제란, 다항 시간내에 최단 비용을 계산할 수 없다고 알려진 문제를 의미합니다.일반적으로 DP 등의 알고리즘을 활용하면, 최적해는 아니더라도 최적해에 근접한 근사치를 빠르고 효율적으로 찾을 수 있다고 알