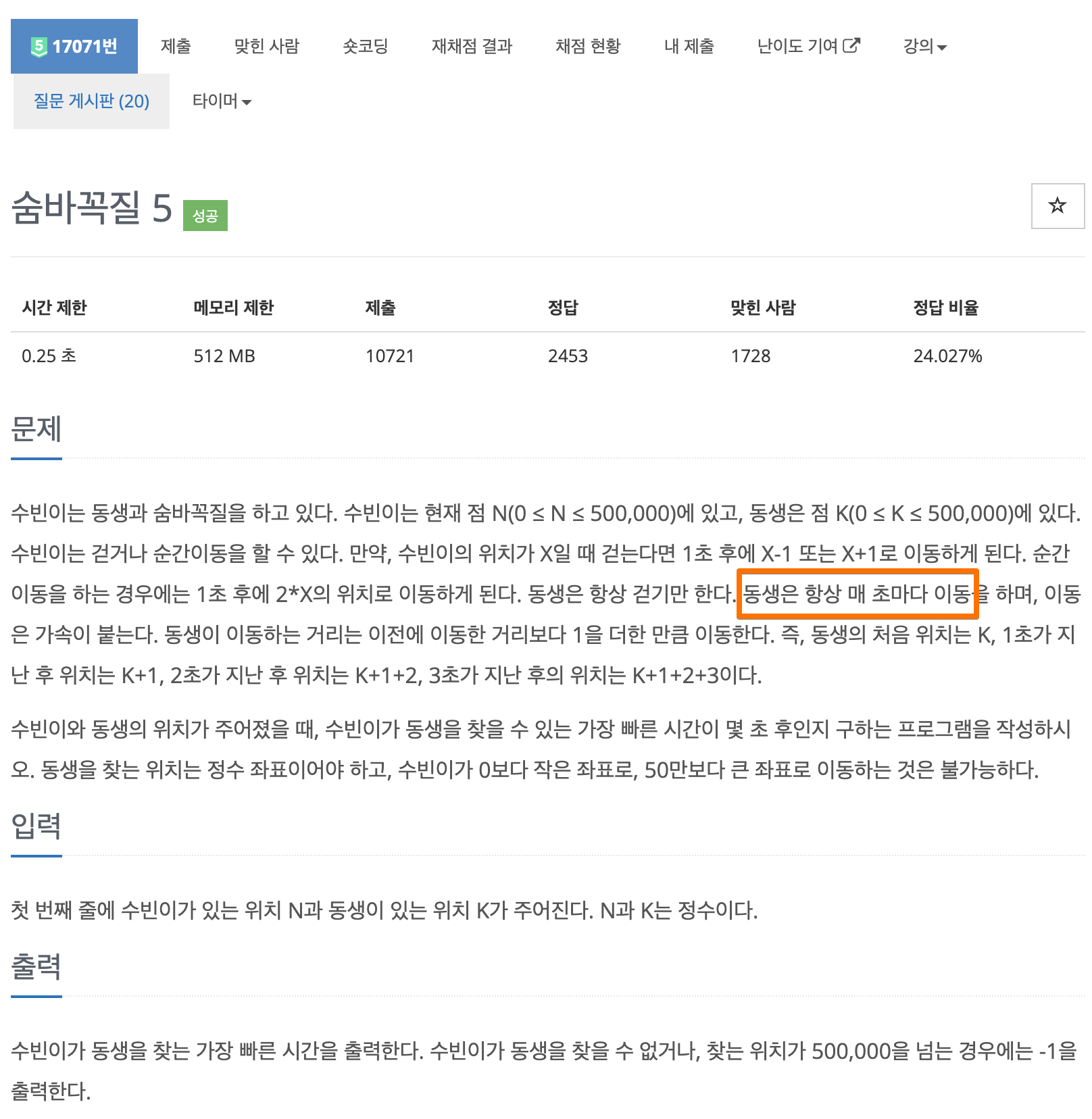
문제

문제 링크

해설

• 동생의 위치가 매 초마다 정방향으로 움직인다는 특수성 때문에 고려해야할 새로운 경우의 수가 생깁니다.

• 바로 가만히 있는게 빠를 수도 있다는 것입니다.

  • 예를 들어, 예제 입력 2의 17 5의 경우
  • 수빈이가 17 -> 16 -> 15 -> 16 -> 15로 좌표 16, 15에서 ±1로 왔다갔다해서 제자리에 있으면 동생은 5 -> 6 -> 8 -> 11 -> 15로 4초 뒤 좌표 15에 도달합니다.
  • 이 문제의 최대 장애물이 바로 이 것입니다. 동생이 움직이기 때문에 반드시 수빈이가 어딘가로 멀리 이동하는 것이 최단 거리를 보장하지 못합니다.

• 위 경우의 수를 고려하려면 어떻게 해야 할까요? 시간을 홀수/짝수로 나눠 생각해보는 겁니다.

  • 만일 어떤 좌표 X에 동생이 t초(홀수)에 도착한다고 생각합시다.
  • 그렇다면 수빈이는 그 좌표 X에 t-2, t-4, … , 홀수초에 미리 도착한 뒤 왔다갔다하며 제자리걸음 하면 동생을 만날 수 있습니다.
  • 반대로 동생이 t초(짝수)에 도착해도 마찬가지겠죠?

• 결과적으로 동생이 갈 수 있는 어떤 좌표 X에 대해

  • 홀수번째 초에 도착했다면, 해당 좌표 X에 수빈이가 홀수번째 초에 미리 도착할 수 있다면 최단거리
  • 짝수번째 초에 도착했다면, 해당 좌표 X에 수빈이가 짝수번째 초에 미리 도착할 수 있다면 최단거리

• 이번에는 방문기록 배열을 visited[2][500'001] 짜리 2차원 배열로 생성합니다. 왜냐하면, 같은 좌표 X라도 홀수번째 초에 도착했을 때와 짝수번째 초에 도착했을 때를 다르게 생각해야 하기 때문입니다.

• BFS 종료조건은 어떻게 될까요?

  1. 이번 loop의 수빈이의 위치가 동생의 위치라면 종료!
  2. 다음 loop의 수빈이가 예상 위치가 동생의 위치라면 종료!
     • 이때, 기존 visited[next_x] = visited[now_x] + 1은
     • visited[홀수/짝수초][next_x] = visited[짝수/홀수초][now_x] + 1이 되겠죠?

코드

#include <iostream>
#include <queue>
using namespace std;

constexpr int MAX = 500'001;
int N, K, visited[2][MAX];

int main() {
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);

    cin >> N >> K;
    if (N == K) { cout << 0; return 0; }

    queue<int> q;
    q.push(N);
    visited[0][N] = 1;

    int t = 1;  // time;
    bool is_they_meet = false;

    while (!q.empty()) {
        K += t;
        if (K >= MAX) break;
        if (visited[t & 1][K]) { is_they_meet = true; break; }

        int qsize = q.size();
        for (int i = 0; i < qsize; i++) {
            int here = q.front(); q.pop();
            for (int there : {here * 2, here + 1, here - 1}) {
                if (there < 0 || there >= MAX || visited[t & 1][there]) continue;
                if (there == K) { is_they_meet = true; break; }
                visited[t & 1][there] = visited[(t + 1) & 1][here] + 1;
                q.push(there);
            }
            if (is_they_meet) break;
        }
        if (is_they_meet) break;
        t++;
    }
    (is_they_meet) ? (cout << t) : (cout << -1);
    return 0;
}

• 참고로 t & 1은 비트연산을 이용한 홀수, 짝수 판별법입니다.
• 홀수는 항상 0번 bit가 1이고, 짝수는 항상0 이므로 1과 AND 연산한 결과로 홀수 짝수를 판별할 수 있습니다.

소스코드 링크

결과