문제

문제 링크

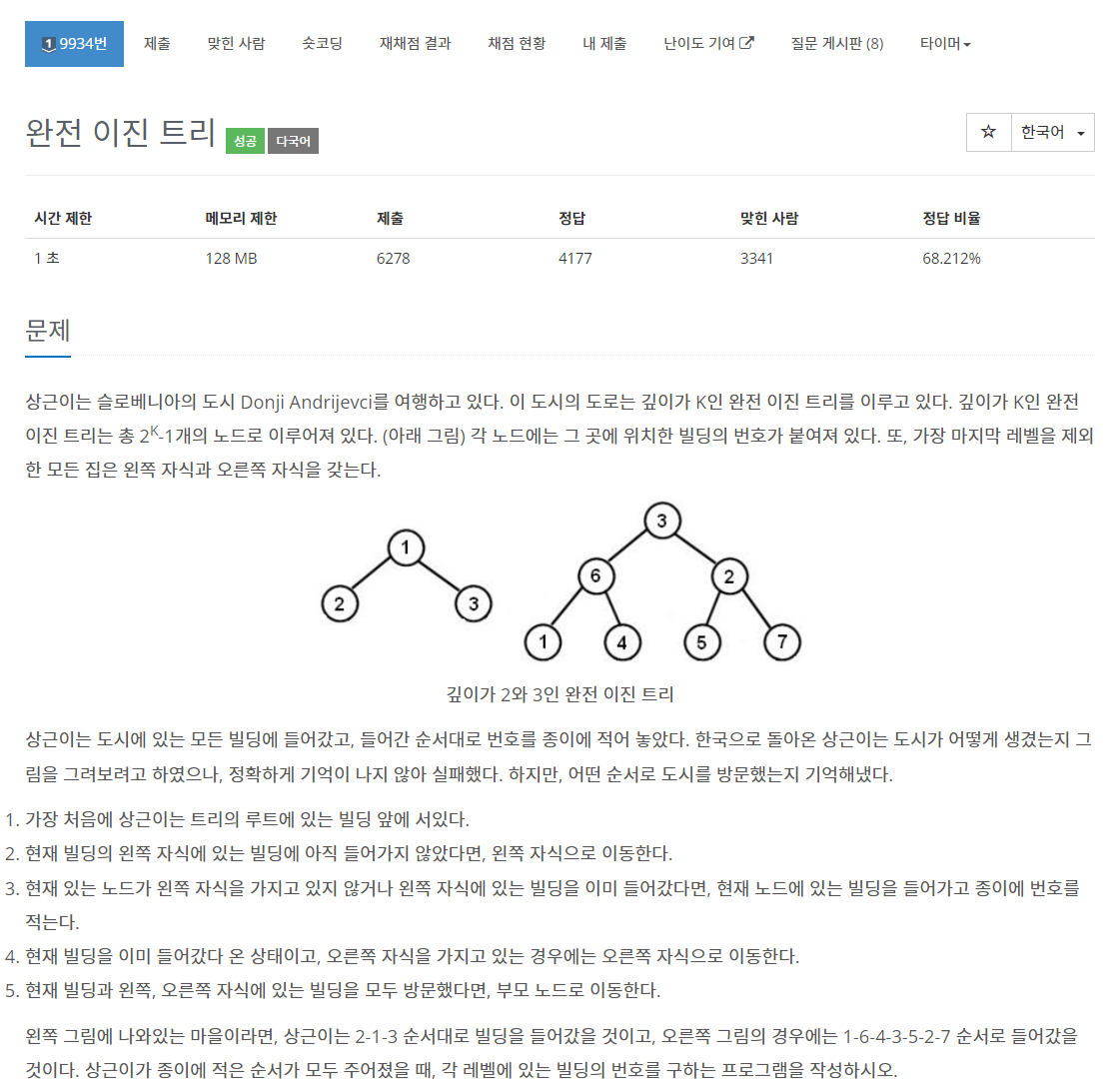
해설

어렵지 않게 in-order 방식으로 입력이 주어지는 문제임을 알 수 있습니다.
이 문제는 두 가지 접근법으로 풀 수 있습니다.

완전이진트리 성질 이용

• 먼저 완전이진트리 성질을 이용해서 푸는 방법입니다.

• 문제에서 주어지는 in-order 방식의 입력을 level 별로 출력하기 위해서는
  

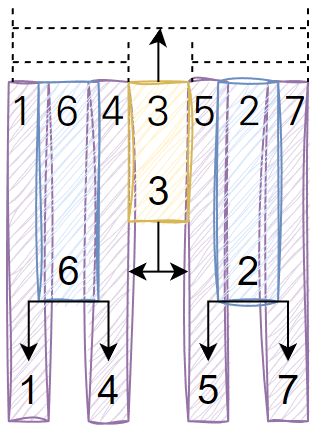
• 위 그림처럼 범위 중 중앙값을 그대로 출력, 좌측절반/ 우측절반을 분할해 재귀를 돌리면 됩니다.

완전이진트리 성질 이용 X

• 완전이진트리 성질을 이용하지 않는 경우,
  • 반대로 임의의 트리를 만든 뒤 in-order 방식으로 변경합니다.
  • 방금 만든 in-order 방식의 트리와 입력값을 비교대조하며 다시 원래 형태의 트리를 만듭니다.
  • 원래 형태의 트리를 토대로 level 별로 출력합니다.
• 말로만 들었을 때는 복잡해보이지만, 코드로 구현하면 복잡하지 않습니다.

do {
    int key;
    cin >> key;
    keys.push_back(key);
    cnt++;
} while (getc(stdin) == ' ');

• 저는 입력값이 포화 완전이진트리가 아니기 때문에 반드시 2의 K제곱개의 입력이 주어지지 않을 것이라 생각했기 때문에 getc() 함수를 이용했습니다.
• 이때, 평소에 여러분이 '입력 개수를 모를 때' 사용하시는 방법을 사용하시면 될 것 같은데, 이상하게 저는 while (cin >> key) 방식이 이번에는 제대로 통하지 않아서 부득이하게 getc(stdin)을 사용했습니다.
• ios::sync_with_stdio(); cin.tie(nullptr); cout.tie(nullptr);은 제거하셔야 getc(stdin)함수를 제대로 사용하실 수 있다는 점 혹시 몰라서 알려드립니다.

코드

완전이진트리 성질 이용

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;

int N, a[1025];
vector<int> ret[11];

void solve(int s, int e, int level)
{
	if (s > e) return;
	if (s == e) { ret[level].push_back(a[s]); return; }
	
	int mid = s + (e - s) / 2;
	ret[level].push_back(a[mid]);
	solve(s, mid, level + 1);
	solve(mid + 1, e, level + 1);
}

int main()
{
	ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
	cin >> N;
	int limit = pow(2, N) - 1;
	for (int i = 0; i < limit; i++) cin >> a[i];
	
	solve(0, limit, 1);
	
	for (int i = 1; i <= N; i++) {
		for (auto j : ret[i]) cout << j << ' ';
		cout << '\n';
	}
	return 0;
}

소스코드 링크

완전이진트리 성질 이용 X

#include <iostream>
#include <vector>
using namespace std;

void make_inorder_tree(const vector<int>& tree, int idx, vector<int>& inorder)
{
	if (idx >= (int)tree.size()) return;
	int lc = 2 * idx, rc = 2 * idx + 1;
	if (lc >= (int)tree.size()) {     // 리프노드일 때
		inorder.push_back(tree[idx]);
		return;
	}
	make_inorder_tree(tree, lc, inorder);
	inorder.push_back(tree[idx]);
	make_inorder_tree(tree, rc, inorder);
}

int main()
{
	int K;
	cin >> K;
	
	vector<int> keys;
	keys.reserve(1 << K);
	int cnt = 0;
	do {
		int key;
		cin >> key;
		keys.push_back(key);
		cnt++;
	} while (getc(stdin) == ' ');
	
	vector<int> tree(cnt + 1);
	for (int i = 0; i <= cnt; i++) tree[i] = i;
	
	vector<int> inorder;
	make_inorder_tree(tree, 1, inorder);

	for (int i = 0; i < cnt; i++) tree[inorder[i]] = keys[i];
	
	int i = 1, level = 1;
	while (level <= K) {
		for (; i < min((1 << level), cnt + 1); i++) cout << tree[i] << ' ';
		cout << '\n';
		level++;
	}
	return 0;
}

• for (int i = 0; i < cnt; i++) tree[inorder[i]] = keys[i]; 이 line이 정답을 만드는 핵심 line입니다.
  

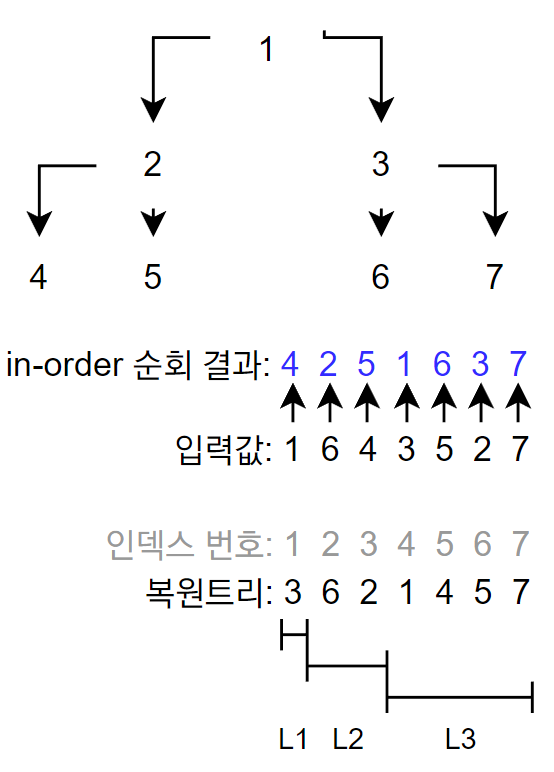
• 인덱스 번호를 key값으로 갖는 완전이진트리를 생성한 뒤 in-order로 순회하며 새로운 in-order 완전이진트리를 생성합니다.

• in-order 트리의 결과는 입력값이 복원됐을 때의 트리 인덱스 번호입니다.

• 복원트리를 1, 2, 4, 8 ... 2의 배수 개수로 출력하면 레벨별로 출력할 수 있습니다.

소스코드 링크

결과