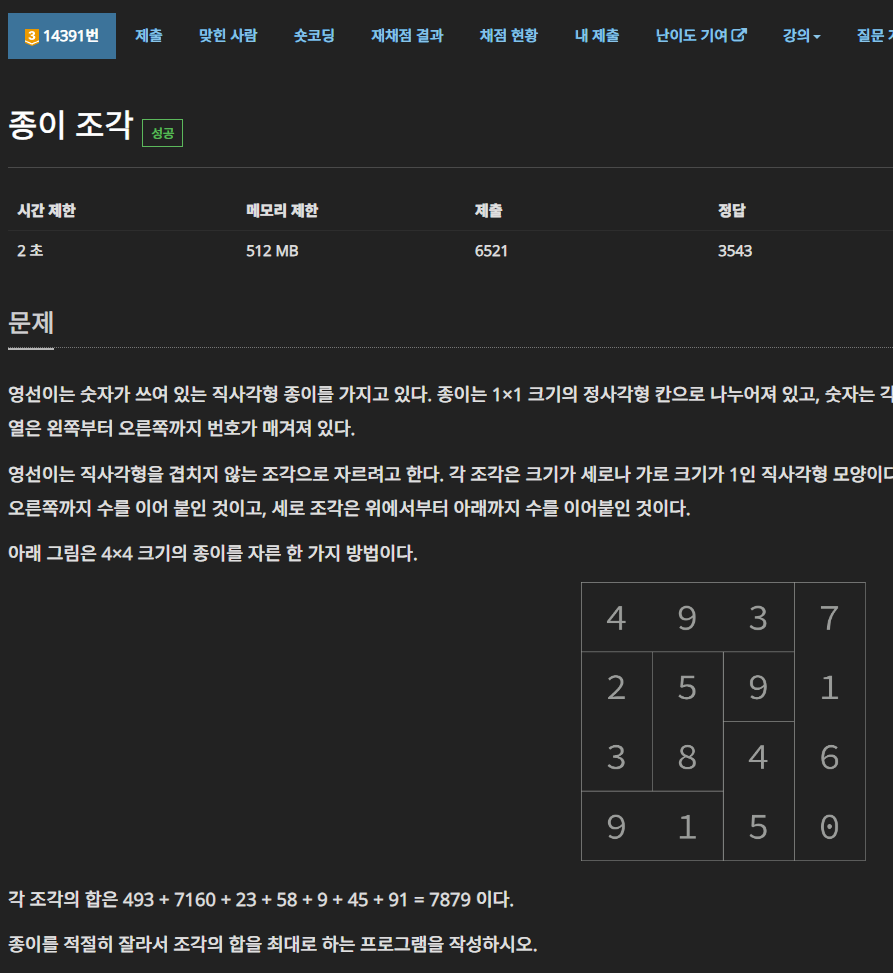
문제

문제 링크

해설

비트마스킹이 익숙하지 않다면, 아이디어가 떠오르지 않아 정말 어려울 문제입니다.

• 최대 크기가 4×4 밖에 안 되지만, 임의의 좌표 (y, x)에서 최대 15가지 경우의 수가 만들어집니다.
• 물론 (y+1, x), (y, x+1)로 갈수록 만들어질 수 있는 경우의 수는 줄어들어 2초 내로 풀 수 있습니다.
• 하지만 굉장히 복잡한 경우의 수를 고려해야 합니다.

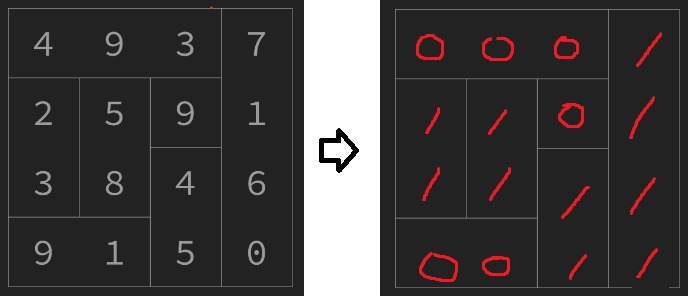
핵심 아이디어는 임의의 칸 (y, x)가 false일 때 가로조각, true일 때 세로조각이라고 가정하는 것입니다.

• 다행히 최대 크기가 4×4 = 16칸이므로 16-bit를 사용해 모든 경우의 수를 표현할 수 있습니다.
• 그러므로 1 << (N * M) 연산으로 모든 가로조각과 세로조각 조합 경우의 수를 구할 수 있습니다.
• 어떤 좌표 (y, x)에 대응하는 bit가 true라면 해당 좌표는 세로조각, false라면 가로조각인 것입니다.
• 결과적으로 가로조각을 따로 계산하고, 세로조각을 따로 계산한 뒤 합산한 것의 최댓값을 구하면 됩니다.

코드

#include <iostream>
using namespace std;

int N, M, paper[4][4];

int main() {
    ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
    cin >> N >> M;
    for (int y = 0; y < N; ++y){
        string row;
        cin >> row;
        for (int x = 0; x < M; ++x)
            paper[y][x] = row[x] - '0';
    }
    int answer = 0;
    for (int i = 0; i < (1 << (N * M)); ++i) {
        int sum = 0;
        // [Case 1] 가로 조합을 계산합니다.
        for (int y = 0; y < N; ++y) {
            int value = 0;
            for (int x = 0; x < M; ++x) {
                if (i & (1 << (M * y + x))) {
                    sum += value;
                    value = 0;
                } else {
                    value = 10 * value + paper[y][x];
                }
            }
            sum += value;
        }
        // [Case 2] 세로 조합을 계산합니다.
        for (int x = 0; x < M; ++x) {
            int value = 0;
            for (int y = 0; y < N; ++y) {
                if (i & (1 << (M * y + x))) {
                    value = 10 * value + paper[y][x];
                } else {
                    sum += value;
                    value = 0;
                }
            }
            sum += value;
        }
        answer = max(answer, sum);
    }
    cout << answer << '\n';
}

소스코드 링크

결과