
문제

해설
( 다양한 아이디어를 적용해야 제한시간 내에 풀 수 있는 어려운 문제였습니다. )
- 피자 A, B가 각각 최대 1,000조각 씩 있기 때문에 아쉽게도 O(N²) 방법으로는 시간 내에 풀 수가 없습니다.
- (1000C1 + 1000C2 + 1000C3 + ... + 1000C999) + (...) 이기 때문입니다.
- (처음에는 가능할 줄 알고
std::set<>을 이용해서 풀었는데 TLE가 났습니다. 참고하시라고 하단에 코드를 첨부합니다.)
- 이 문제는 특정 값을 구하는 경우의 수가 중요하지, 특정 값이 중요한 것이 중요한 것이 아닙니다.
- 즉, A에서 어떤 조합을 만들거나, B에서 어떤 조합을 만들거나, A와 B에서 어떤 조합을 만든 것이 목표한 값과 같은가?
- 이것을 계속해서 검사하는 것보다는,
- A에서 만들수 있는 모든 조합에서 각 수가 등장하는 횟수를 카운팅한 뒤, 목표한 값이 몇 번 등장했는지 출력하면 됩니다.
- 즉, 해쉬를 쓰면 됩니다.
- 이때, 피자가 원형 구조입니다.
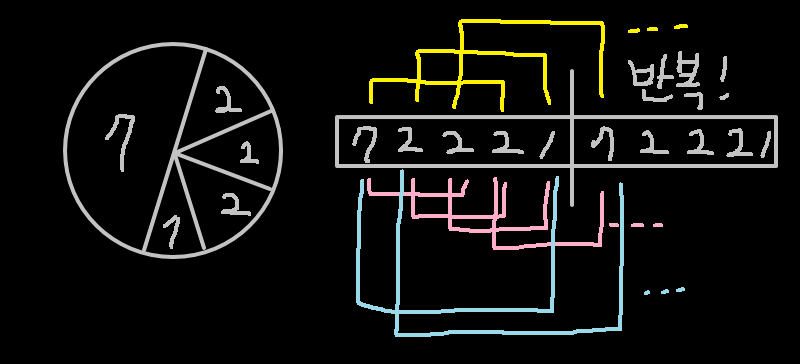
- 원형구조는 다루기가 까다롭기 때문에 모듈라 연산을 쉽게 사용할 수 있는 구조가 아니라면, 위와 같이 전체를 선으로 2번 이어붙여서 생각하면 훨씬 편합니다.
- 그리고, 연속된 조각의 크기 합은 곧 누적합이므로 각 피자 A, B의 누적합을 구합니다.
- 누적합을 구했다면, 2중 for문을 사용해서 모든 조합의 차를 계산한 뒤
std::unordered_map<int, int>에 넣습니다. 위에서도 해시를 사용하겠다고 말씀드렸죠? - 마지막으로 ⓐ A에서 T를 만드는 경우, ⓑ B에서 T를 만드는 경우, ⓒ A와 B를 합쳐서 T를 만드는 경우를 각각 더해서 답을 출력하면 됩니다.
코드
#include <bits/stdc++.h>
using namespace std;
constexpr int MAX = 1'001;
int T, M, N, answer;
int A[MAX], B[MAX], psumA[2 * MAX], psumB[2 * MAX];
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> T >> M >> N;
for (int i = 1; i <= M; ++i) {
cin >> A[i];
psumA[i] = psumA[i - 1] + A[i]; // Partial sum of A
}
for (int i = M + 1; i <= 2 * M; ++i) psumA[i] = psumA[i - 1] + A[i - M];
for (int i = 1; i <= N; ++i) {
cin >> B[i];
psumB[i] = psumB[i - 1] + B[i]; // Partial sum of B
}
for (int i = N + 1; i <= 2 * N; ++i) psumB[i] = psumB[i - 1] + B[i - N];
unordered_map<int, int> cntA;
for (int i = 1; i <= M; ++i) {
for (int j = i; j <= (i - 1) + M; ++j) {
cntA[psumA[j] - psumA[j - i]]++;
if (i == M) break; // 길이가 M인 부분부열은 1개밖에 없으므로
}
}
unordered_map<int, int> cntB;
for (int i = 1; i <= N; ++i) {
for (int j = i; j <= (i - 1) + N; ++j) {
cntB[psumB[j] - psumB[j - i]]++;
if (i == N) break; // 길이가 N인 부분수열은 1개밖에 없으므로
}
}
// 1. 각 A, B에서만 T를 만드는 경우 + 2. A + B를 조합하는 경우
answer = cntA[T] + cntB[T];
for (int i = 1; i < T; ++i) answer += (cntA[i] * cntB[T - i]);
cout << answer;
}결과

