문제
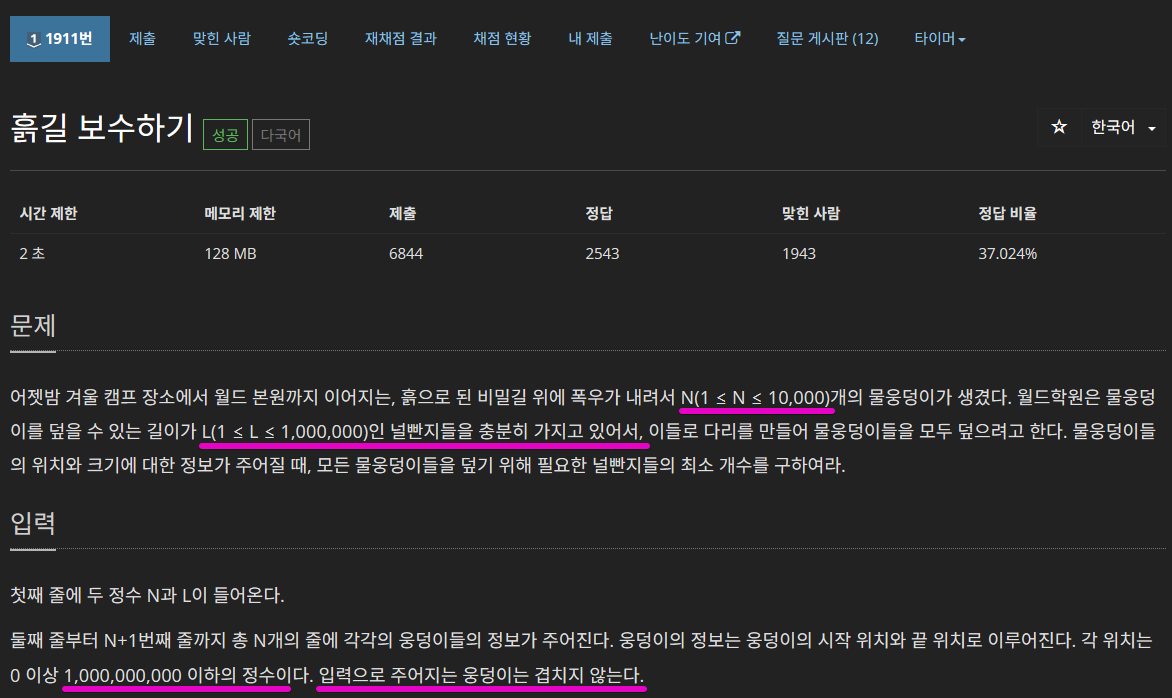
문제 링크
해설
- 대표적인 라인스위핑 문제 중 하나로, 이 문제(문제링크, 해설링크)와 유사합니다.
- 웅덩이의 범위가 10억까지이므로 메모리 제한 때문에 절대 좌표상으로 나타낼 수 없습니다.
- 따라서, 입력받은 물웅덩이를 시작점에 따라 오름차순으로 정렬한 뒤, 시작점부터 끝점까지 널빤지를 하나씩 놓으면서 모든 물웅덩이를 탐색한다면 O(N)에 최적해를 구할 수 있습니다.
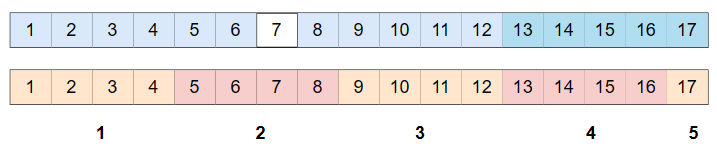
- 널빤지를 최소한으로 사용하기 위해서는
- 널빤지는 웅덩이의 시작점부터 놓아야합니다.
- 널빤지의 끝점이 다른 웅덩이와 겹친다면, 계속 놓으면 됩니다.
- 널빤지의 끝점이 다른 웅덩이와 겹치지 않는다면, 정답에 방금까지 웅덩이를 덮느라 놓았던 널빤지 개수를 증감합니다.
- 웅덩이에 들어가는 널빤지 개수를 수학적으로 개산하면,
ceil(웅덩이 끝점 - 널빤지 끝점) 입니다.
- 햇갈리실 수 있습니다. 이해합니다.
- 위에서 말씀드렸지만, 방금 놓은 널빤지가 이번에 새로 시작하는 다른 웅덩이의 시작점을 넘어서 겹칠 수 있습니다.
- 위 그림에서도 2번째 널빤지가 새로운 웅덩이랑 겹친것을 볼 수 있습니다.
- 따라서 웅덩이의 길이는 웅덩이의 끝점 ~ 웅덩이의 시작점이 아니라, 웅덩이의 끝점 ~ 널빤지의 끝점입니다.
ceil()을 붙인 이유는, 웅덩이를 덮기 위해서는 무조건 소수점을 올림해야 하기 때문입니다. 남는 부분이 있어서는 안 되겠지요?
코드
#include <bits/stdc++.h>
using namespace std;
int main() {
cin.tie(0)->sync_with_stdio(0);
int N, L;
cin >> N >> L;
vector<pair<int, int>> vec(N);
for (int i = 0; i < N; ++i) cin >> vec[i].first >> vec[i].second;
sort(begin(vec), end(vec));
int answer = 0, curPos = vec.front().first;
for (const auto& pos : vec) {
if (curPos < pos.first) curPos = pos.first;
int cnt = ceil(static_cast<double>(pos.second - curPos) / L);
answer += cnt;
curPos += cnt * L;
}
cout << answer;
}
소스코드 링크
결과





