문제
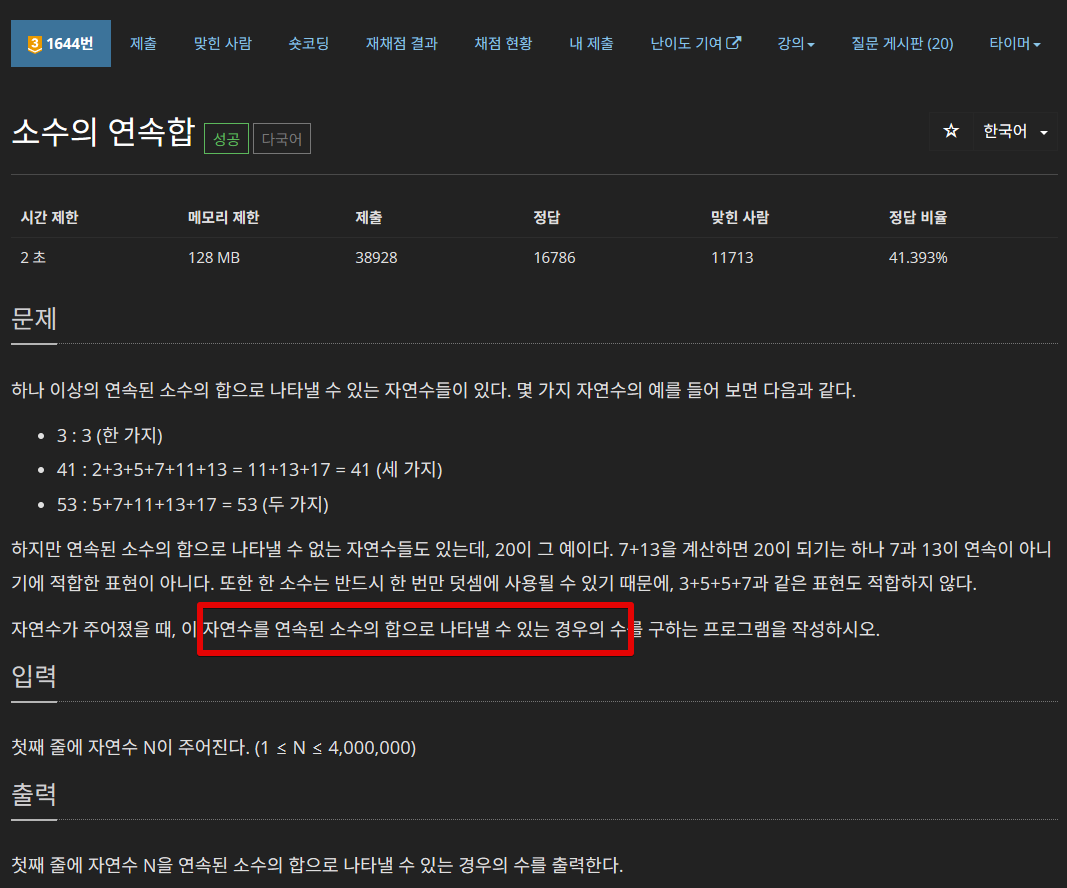
문제 링크
해설
- 우선 소수를 빠르게 판별하는 알고리즘으로는 '에라토스테네스의 체'가 있습니다.
- 에라토스테네스의 체는 O(log(N)에 N까지의 소수를 판별할 수 있기 때문에 약 3, 4줄 밖에 안 되므로 하나의 공식처럼 코드 덩어리를 외워두는 것이 좋습니다.
- 입력되는 자연수 N이 400만 까지이므로 연속되는 구간의
- 연속되는 구간의 시작점과 끝점을 바탕으로 경우의 수를 구하고자 하는 아이디어는 굉장히 좋습니다.
- 하지만, 이때 시작점과 끝점을 for문 2개를 사용해 갱신하면, 시간복잡도가 O(N²)이라 시간 내에 풀 수 없습니다.
- 그러므로, 현재까지의 연속합 결과와 구하고자 하는 값 N을 비교해서 시작점과 끝점을 이동하면서 for문 1개로 O(N)에 풀어야 합니다.
- 즉, 투포인터로 문제를 빠르게 풀 수 있습니다.
- 구간 내 연속합
sum이 N보다 크다면, 제일 작은 양수를 연속합에서 제거하는 것이 좋습니다. → 즉, 시작점을 오른쪽으로 당겨줍니다.
- 구간 내 연속합
sum이 N보다 작다면, 제일 큰 양수를 연속합에 더하는 것이 좋습니다. → 즉, 끝점을 오른쪽으로 당겨줍니다
코드
#include <bits/stdc++.h>
using namespace std;
int main() {
cin.tie(0)->sync_with_stdio(0);
int N;
cin >> N;
vector<bool> isPrime(N);
for (int i = 2; i <= N; ++i) {
if (isPrime[i]) continue;
for (int j = i + i; j <= N; j += i) isPrime[j] = true;
}
vector<int> prime;
prime.reserve(N >> 3);
for (int i = 2; i <= N; ++i)
if (!isPrime[i]) prime.emplace_back(i);
int ans = 0, sum = 0, left = 0, right = 0;
while (true) {
if (sum >= N) sum -= prime[left++];
else if (right == prime.size()) break;
else sum += prime[right++];
if (sum == N) ans++;
}
cout << ans;
}
소스코드 링크
결과




