문제

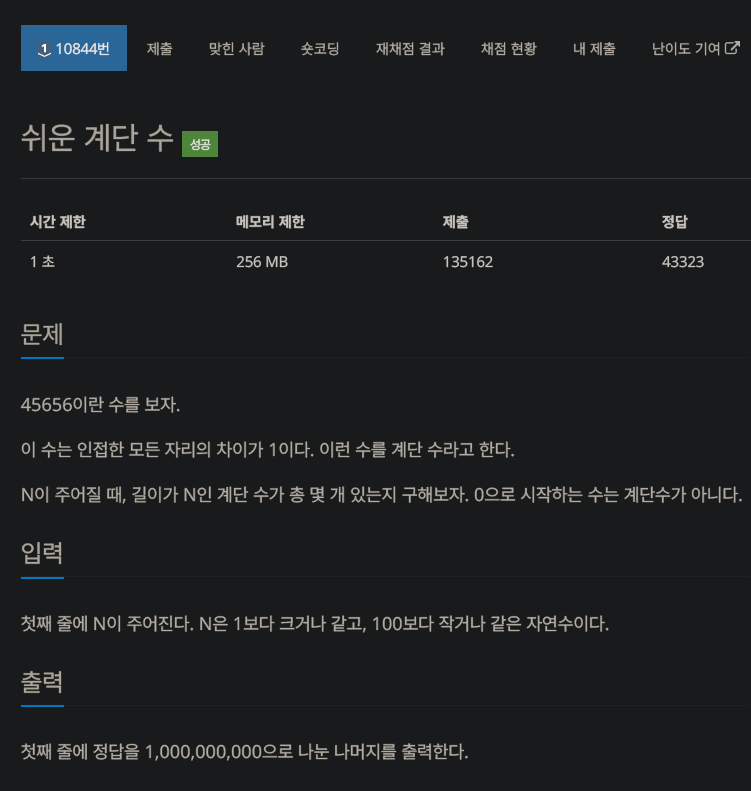
문제 링크

해설

• 길이가 2 이상일 때부터는 가장 앞자리에 0이 올 수 없으며,
• 계단수가 되기 위해서는
  • 0은 무조건 1로 증가하는 방향만 고려해야 하고,
  • 9는 무조건 8로 감소하는 방향만 고려해야 합니다.
• 그러므로, 길이가 N - 1일 때 맨 앞자리에 어떤 수가 오느냐에 따라 N일 때 올 수 있는 숫자의 상태가 달라집니다. ▶ 【길이, 마지막 자리 숫자】
• 따라서, DP[N][11]로 메모이제이션 2차원 배열을 정의합니다. ([10] 인덱스를 마련하는 이유는 '코드'란에서 후술하겠습니다.)
• 길이가 N이고 마지막 수가 K인 계단수는,
  • 길이가 N - 1이고 마지막 수가 K - 1인 계단수 개수와
  • 길이가 N - 1이고 마지막 수가 K + 1인 계단수 개수를 합치면 됩니다.

코드

#include <bits/stdc++.h>
using namespace std;
constexpr int MOD = 1'000'000'000;

int N, DP[101][11];

int main() {
	cin.tie(0)->sync_with_stdio(0);
	cin >> N;
	for (int i = 0; i < 10; ++i) DP[1][i] = 1;
	for (int len = 2; len <= N; ++len)
		for (int num = 0; num <= 9; ++num)
			DP[len][num] = (num != 0) ? ((DP[len - 1][num - 1] + DP[len - 1][num + 1]) % MOD) : (DP[len - 1][num + 1]);
	int ans = 0;
	for (int i = 1; i <= 9; ++i) ans = (ans + DP[N][i]) % MOD;
	cout << ans;
}

• 앞서 0은 무조건 증가하는 방향, 9는 감소하는 방향을 고려해야 한다고 설명했습니다.
• 2중 for문을 보면 (num != 0)으로 마지막에 오는 수가 0인지 아닌지만 검사합니다.
  • 메모이제이션 배열이 전역에 생성돼있으므로 인덱스 [10]은 항상 0을 가집니다.
  • 따라서, DP[len - 1][num + 1]이 가리키는 값이 DP[len - 1][10]이어도 결국 0이므로 상관없습니다.
  • 정리하면, if문 하나 줄여서 코드를 간단하게 작성하기 위해 사용했습니다.

소스코드 링크

결과