문제

문제 링크

해설

• LCS는 대표적인 DP 문제로 푸는 방법이 정해져있으니 외워두는 것이 좋습니다.
• 공집합도 부분집합의 하나이므로, 빈문자(공백)를 포함해서 DP[첫번째 문자열 길이 + 1][두번째 문자열 길이 + 1] 크기의 2차원 메모이제이션 배열을 생성합니다.
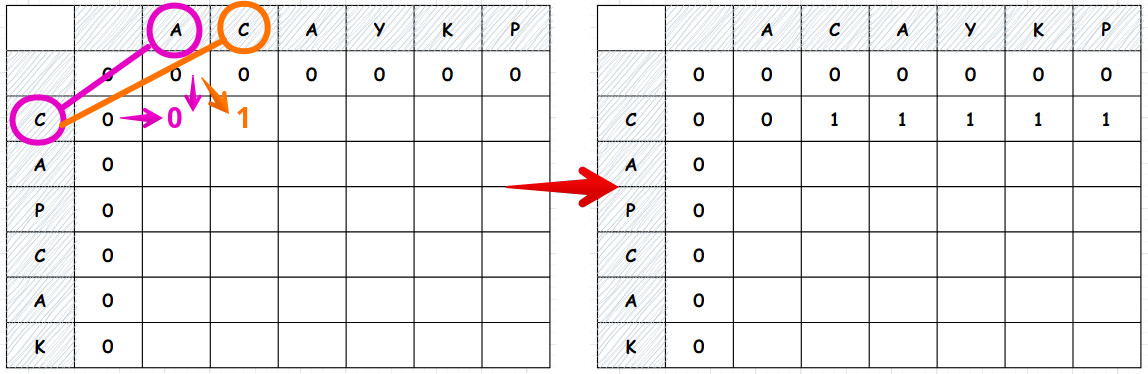
• 빈문자는 부분집합의 일부지만, 부분수열의 일부라고는 볼 수 없으므로, 0번 행과 0번 열은 LCS길이를 0으로 초기화 합니다. (상단 왼쪽 그림 참고)
• 첫 번째 글자를 비교합시다.(핑크색)
  • A와 C는 서로 다르므로, y축으로 윗칸, x축으로 왼쪽칸 중 큰 쪽을 가져갑니다.
• 두 번째 글자를 비교합니다.(주황색)
  • C와 C는 같으므로 현재 값과 왼쪽 대각선값 + 1한 값 중 큰 쪽을 가져갑니다.
  • 문자열 AC와 문자열 C는 LCS가 1이므로 값이 맞는것을 확인할 수 있습니다.
• 위 내용을 식으로 정리하면,

if (글자 다르면)
    DP[y][x] = max(DP[y][x - 1], DP[y - 1][x]);
else
    DP[y][x] = max(DP[y][x], DP[y - 1][x - 1]);

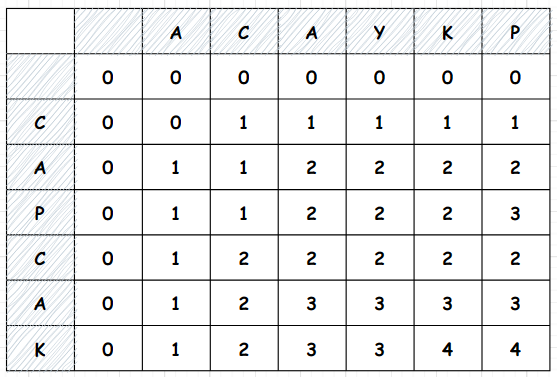
• 이 규칙성을 유지하면서 마지막까지 진행한 뒤 우측 하단값을 출력하면 됩니다.
  

코드

#include <iostream>
using namespace std;

string A, B;
int lenA, lenB;
int DP[1002][1002];

int main() {
	cin.tie(0)->sync_with_stdio(0);
	cin >> A >> B;
	lenA = A.size(), lenB = B.size();
	for (int y = 1; y <= lenB; ++y)
		for (int x = 1; x <= lenA; ++x)
			DP[y][x] = (B[y - 1] == A[x - 1]) ? DP[y - 1][x - 1] + 1 : max(DP[y - 1][x], DP[y][x - 1]);
	cout << DP[lenB][lenA];
}

소스코드 링크

결과