[컴퓨터구조 요약 정리] 2. Digital System Basics

2.1. 수 체계

• 대표적으로 디지털 시스템에서 사용되는 수체계 = 10진수(Decimal)와 2진수(Binary)
• 10진수와 2진수 사이의 conversion을 자유롭게 하는 능력이 중요하다.
• $2^{10} = 1K(1,024)$, $2^{20} = 1M (1,048,576)$, $2^{30} = 1B(1,073,741,824)$로 대략적으로 표현할 수 있다.
• Bit는 0과 1로 이루어진 2진수 수 하나를 의미한다.
  • 가장 왼쪽에 bit를 MSB(Most significant bit)라 부른다.
  • 가장 오른쪽에 있는 수를 LSB(Least Significant bit)라고 한다.
  • 설명을 편하게 하기 위해 왼쪽-오른쪽으로 구분했지만 반드시 맞는 건 아니다. 2진수 표기 방법(Endianness) 있는데, 이 방향에서 가장 앞쪽 bit를 MSB, 뒤쪽 bit를 LSB라고 부르는 것이 맞다.
• Bytes는 8개의 bits, Nibbles는 4개의 bits로 구성돼있음.

2’s complement

• 2의 보수는 모든 bit를 반전시킨 다음에 1을 더해줘서 구한다.**
• Signed binary number일 경우에는 MSB가 0이면 양수, 1이면 음수를 나타낸다.
• Singed n-bit number의 범위는 $[-2^{n-1}, \ 2^{n - 1} - 1]$ 이다.

2.2. Binary 연산

• 2진수의 덧셈은 sign 여부에 따라 덧셈 방법이 다르다.
  • Unsigned binary의 덧셈은 10진수의 덧셈처럼 자리 올림을 해주며 더하면 된다.
  • Signed binary의 덧셈은 2의 보수를 취해서 더한다.
• 정해진 bit 수를 초과하는 경우, carry-out bit가 발생한다.
• 두 수의 자릿수가 맞지 않아서 어느 한 수의 bit를 확장시켜줘야 하는 경우가 있다.
  • Signed binary는 Sign-Extension을 한다. 부호비트를 그냥 더 늘려준다.
    • ex1) 3 = 0011 = 0000 0011
    • ex2) -5 = 1011 = 1111 1011
  • Unsigned binary는 Zero-Extension을 한다. MSB에 이어서 0을 추가시켜주면 된다.
    • ex1) 3 = 0011 = 0000 0011
    • ex2) -5 = 1011 ≠ 0000 1011 (11)
  • Arithmetic 한 수로 볼 것인지, logical 한 수로 볼 것인지에 따라 extension 방법이 달라진다.
    • 0011을 3으로 볼 수도 있지만, 4개의 자리가 있고 첫 두 자리는 비어있고, 뒷자리는 차있는 것으로 볼 수도 있다.
    • 논리적인 자릿수가 더 중요할 경우에는 수의 자릿수를 그대로 유지한 체로 bit수를 늘려주는 것이 중요하다.

2.3. Digital building blocks

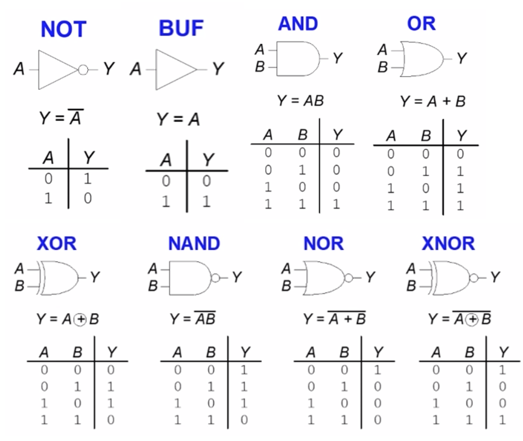
• 우리는 위 8가지 logical block을 가장 일반적으로 사용한다.
• 각각에 대한 진리표와 상세한 설명은 너무나 당연한 내용이라 생략하고자 한다.

Adder

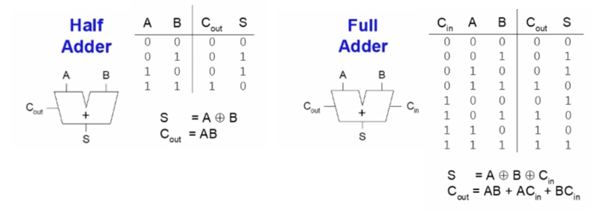
1. Half adder
   • 두 개의 입력을 받은 뒤 더해서 Sum과 Carry-out bit를 내보내는 연산을 수행한다.
   • Sum은 A와 B의 XOR 연산으로, Carry-out은 AND 연산으로 나타낼 수 있다.
   • 
   • XOR은 NAND 4개로, AND는 NAND 2개로 표현할 수 있고, HA는 NAND 5개로 표현할 수 있다.
2. Full adder
   • Carry-in bit를 포함한 3개의 입력을 받아 계산한다.
   • Sum은 A와 B의 XOR 연산의 Cin의 XOR 연산으로, Cout은 각각의 AND 연산끼리의 OR 연산으로 구할 수 있다.
   • 
   • FA는 NAND 8개로 표현할 수 있다.

Adder의 종류

1. Ripple Carry Adder (RCA) - 느림

   • 가장 단순한 구조의 multi-input adder로, 여러 개의 FA를 직렬로 연결한 구조다.

   • 하나의 FA에서 나오는 Cout이 다음번 FA의 Cin으로 들어가며 ripple되는 특성을 가지고 있다.

   • 구조적으로 단순하다는 장점이 있으나 critical delay가 매우 길어진다는 단점이 있다.

   • $t_{RCA} = Nt_{FA}$ 로 표현할 수 있다.

2. Carry-Lookahead Adder (CLA) - 빠름

   • Ripple 되는 carry bit를 조금 더 빠르게 처리하기 위해서 만들어진 adder다.
   • Cout은 입력 A와 B가 모두 HIGH 거나 (Carry out을 generate한다고 표현), A 또는 B가 HIGH고 Cin이 HIGH일 때 발생 (Carry out을 propagate한다고 표현)한다.
   • 식으로 나타내면, $C_i = A_iB_i + (A_i + B_i)C_{i-1} = G_i + P_iC_{i-1}$이다.
   • 따라서 $C_{i-1}, \ C_{i-2} ...$ 이런 식으로 재귀적으로 식을 대입하면, $G, P, C$에 대한 일반식을 구할 수 있다.
   • 그러므로 i-bit에 대한 계산 결과를 일반식을 이용해서 주어진 carry-in에 대해 단번에 결과값을 계산할 수 있어서 carry bit의 ripple을 줄여 critical delay를 줄인다. (i.e. 만일 32-bit 연산에 4-bit 짜리 CLA block을 8개 사용한다면 31번의 ripple에서 7번으로 줄일 수 있다.)
   • $t_{CLA} = t_{pg} + t_{pg \ block} + k$
   • 일반적으로 연산하는 bit의 길이가 16미만일 경우 RCA가 CLA보다 빠르고, 16이상일 경우 CLA가 더 빠르다. CLA는 반드시 P와 G를 미리 계산해야하기 때문이다.
   • 예제) 32-bit 연산에 대해 RCA와 CLA (4-bit block)를 비교하시오.
     단, $t_{FA} = 300ps, \ 2 \ input \ gate \ delay = \ 100ps$이다
     • RCA는 결과값 반환에 32번의 FA를 계산하게 되므로 32 * 300ps = 9.6ns가 소요된다.
     • CLA는 결과값 반환에 3.3ns가 소요된다.
     • 즉, 단순히 adder의 구조만 개선해도 동작 주파수를 3배 가까이 끌어올릴 수 있다!

3. Prefix Adder (PA) - 매우 빠름

ALU에 대한 이야기

Shifter에 대한 이야기

• Logical shifter: 논리적으로 쉬프트 하면서 생기는 빈 공간을 0으로 채운다.
• Arithmetic shifter: 쉬프트 하면서 생기는 빈 공간을 이전 MSB로 채운다.
• Rotator: 쉬프트 하면서 이전 LSB 또는 MSB (끝 쪽 bit)를 앞으로 옮겨준다.

Counter에 대한 이야기 - Sequential circuit을 이용하게 된다.