
3.1. Overflow
두 양수 또는 두 음수를 더할 때 overflow가 발생할 가능성이 있다.
- 두 양수를 더했는데 sign이
1이면 overflow가 발생한 것이다. - 두 음수를 더했는데 sign이
0이면 overflow가 발생한 것이다.
부호가 다른 두 수를 뺄 때 overflow가 발생할 가능성이 있다.
- 음수에서 양수를 빼는 행위는 두 음수를 더하는 행위와 같다.
- 양수에서 음수를 빼는 행위는 두 양수를 더하는 행위와 같다.
3.2. Multiply (곱셈)
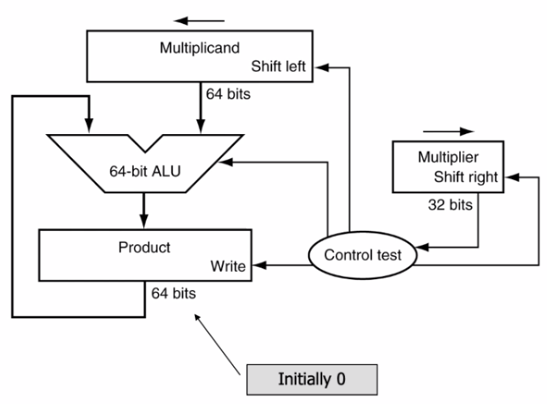
첫 번째 입력을 multiplicand, 두 번째 입력을 multiplier, 결과를 product라고 부른다.
- Multiplier의 LSB가
0인지,1인지 검사한다.0이라면, pass1이라면, 지금까지 계산된 product에 multiplicand를 더해준다.
- Multiplicand를 왼쪽으로 한 칸 shift 해준다.
- Multiplier를 오른쪽으로 한 칸 shift 해준다.
- 1~3 과정을 32번 반복한다. (32-bit 연산이므로)
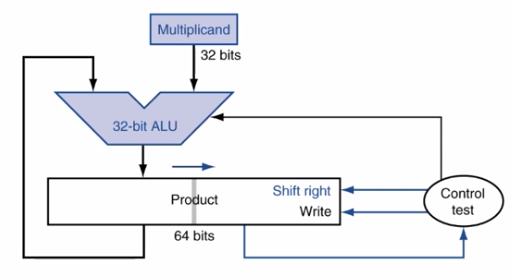
위 구조를 조금 더 단순하게 만들 수 있다.
Multiplicand나 multiplier를 shift 하지말고 Product를 shift하면 multiplicand를 32-bit register에 저장할 수 있다.
따라서, 사칙연산에 대해 모두 32-bit register만 사용하므로 ALU도 64-bit에서 32-bit로 크기가 줄어 더 경제적이게 된다.
여기서 배울 점은, 약간의 아이디어로 ALU 또는 block을 개선한다면, 구조적으로나 성능면으로나 아주 큰 이득을 얻을 수 있다는 점이다.
더욱 빠른 곱셈을 위해서는 adder를 여러 개 사용해서 parallel하게 연산하는 것이다.
HW size나 complexity는 증가하겠지만, 속도는 빨라지게 된다.
3.3. Division (나눗셈)
나눗셈은 고려해줘야 할 사항이 많아서 가장 까다로운 연산자다.
지금까지 다룬 덧셈, 뺄셈, 곱셈은 두 개의 입력에 대해 단일 결과가 반환됐지만, 나눗셈은 두 개의 결과 (몫, 나머지)를 반환해야 하며 divide by zero 등도 신경써줘야 한다.
게다가 나눗셈은 parallelism도 이용할 수 없다. 물론 'SRT division' 처럼 빠른 나눗셈을 가능하게 하는 방법도 있지만 하드웨어가 매우 복잡해지며 그래도 여러 세부 과정이 필요하다.
