매우빠른요약

그래프 구조 데이터에 대해서 데이터 증강에 대한 연구가 미비, 그래서 해보았다. 증강방법과 학습방법에 따라 다양한 실험을 수행하였다.
사용한 증강방법은 노드 드롭, 엣지 섭동, 어트리뷰션 마스킹, 서브그래프이다. 학습과정은 그래프가 들어오면 2개의 증강함수에 넣어서 2개의 증강된 그래프로 바꾸고, 이를 gnn에 넣은 후 latent vector를 구한 뒤 이들을 contrastive loss로 계산하여 학습한다.

Abstract

그래프 구조 데이터에 대한 일반화, 전송 가능 및 강력한 표현 학습은 현재 그래프 신경망(GNN)의 과제로 남아 있다. 이미지 데이터를 위한 CNN(Convolutional Neural Network)을 위해 개발된 것과 달리 GNN에 대한 자체 지도 학습 및 사전 훈련은 미비하다. 본 논문에서는 그래프 데이터의 감독되지 않은 표현을 학습하기 위한 그래프 대조 학습(GraphCL) 프레임워크를 제안한다. 우리는 먼저 다양한 이전을 통합하기 위해 네 가지 유형의 그래프 증강을 설계한다. 그런 다음 우리는 여러 데이터 세트에 대한 다양한 그래프 증강 조합의 영향을 네 가지 다른 설정(준지도, 비지도 및 전송 학습과 적대적 공격)에서 체계적으로 연구한다. 결과는 확대 범위를 조정하거나 정교한 GNN 아키텍처를 사용하지 않더라도 GraphCL 프레임워크가 최첨단 방법에 비해 비슷하거나 더 나은 일반화 가능성, 전달 가능성 및 견고성의 그래프 표현을 생성할 수 있음을 보여준다. 또한 매개 변수화된 그래프 확대 범위와 패턴의 영향을 조사하고 예비 실험에서 추가적인 성능 향상을 관찰한다.

Introduction

이웃 집계 체계(aggregation)를 따르는 그래프 신경망(GNN)은 그래프 구조 데이터에 점점 더 인기가 있는 모델이 되어가고 있다. 노드 또는 링크 분류, 링크 예측 및 그래프 분류와 같은 그래프 기반 작업에서 최첨단 성능을 달성하기 위해 수많은 GNN 변형이 제안되었다. 흥미롭게도, 그래프 수준 작업의 대부분의 시나리오에서 GNN은 감독 하에 종단 간 훈련을 받는다. GNN의 경우 기울기 소실/폭발로 어려움을 겪는 심층 아키텍처를 훈련하는 데 정규화 장치로 일반적으로 사용되는 기술인 (자체 지도) 사전 교육에 대한 탐색이 거의 없다. 흥미로운 현상의 배경에는 에서 보듯이 대부분의 연구된 그래프 데이터 세트의 크기가 종종 제한되고 GNN은 종종 과잉 평활이나 "정보 손실"을 피하기 위해 얕은 아키텍처를 가지고 있기 때문일 수 있다. 그러나 우리는 GNN 사전 훈련 계획을 탐구할 필요성을 주장한다. 작업별 레이블은 그래프 데이터 세트에 대해 매우 부족할 수 있으며(예: 습식 실험실 실험을 통한 생물학 및 화학 레이블링에서는 종종 리소스 및 시간 집약적임), 사전 훈련은 CNN(Convolutional Neural Network)에서와 같이 문제를 완화하는 유망한 기술이 될 수 있다.

GNN 사전 훈련이 부족한 추측된 이유에 대해: 첫째, 실제 그래프 데이터는 거대할 수 있고 심지어 벤치마크 데이터 세트도 최근 커지고 있다. 둘째, 얕은 모델의 경우에도 사전 훈련은 더 나은 일반화와 관련된 로컬 최소값 주변의 "더 나은" 유인 구역에서 매개 변수를 초기화할 수 있다. 따라서, 우리는 GNN 사전 훈련의 중요성을 강조한다.이미지에 대한 CNN과 비교하여 그래프 구조 데이터에 대한 GNN 사전 훈련 체계를 설계하는 데는 고유한 과제가 있다. 이미지의 기하학적 정보와 달리, 그래프는 다양한 성질을 가진 원시 데이터(예: 화학적으로 결합된 원자 및 사회적으로 상호 작용하는 사람들의 네트워크로 만들어진 분자)의 추상화된 표현이기 때문에 다양한 맥락의 풍부한 구조화된 정보가 그래프 데이터에 존재한다. 따라서 일반적으로 다운스트림 작업에 유익한 GNN 사전 훈련 계획을 설계하는 것은 어렵다. 그래프 수준 작업에 대한 기초적인 GNN 사전 훈련 계획은 정점 인접 정보(예: 네트워크 임베딩의 GAE 및 GraphSAGE)를 재구성하는 것이다. 이 계획은 항상 유익하지 않은 근접성을 지나치게 강조하고 구조 정보를 손상시킬 수 있기 때문에 매우 제한적일 수 있다. 따라서 그래프 구조화된 데이터에서 매우 이질적인 정보를 캡처하기 위해 잘 설계된 사전 훈련 프레임워크가 필요하다.

최근 시각적 표현 학습에서 대조적 학습에 대한 관심이 다시 급증하고 있다. 수작업으로 만든 자기 지도 handcrafted pretext task는 설계 시 휴리스틱에 의존하므로 학습된 표현의 일반성을 제한할 수 있다. 대조적으로, 대조 학습(Contrastive learning)은 데이터 또는 작업별 증강을 활용하여 원하는 특징 불변성을 주입하는 서로 다른 증강 뷰에서 기능 일관성을 최대화하여 표현을 학습하는 것을 목표로 한다.사전 훈련 GCN으로 확장되면 이 프레임워크는 앞서 언급한 근접 기반 사전 훈련 방법의 한계를 잠재적으로 극복할 수 있다. 그러나 시각적 표현 학습 외부에서 직접 적용되는 것은 간단하지 않으며 그래프 표현 학습에 상당한 확장을 요구하여 아래의 혁신으로 이어진다.

Contribution

본 논문에서는 그래프의 데이터 이질성 문제를 해결하기 위해 GNN 사전 훈련을 위한 증강과 대조 학습을 개발했다.
(i) 데이터 증강은 대조적 학습의 전제 조건이지만 그래프 데이터에서 충분히 탐구되지 않기 때문에, 우리는 먼저 네 가지 유형의 그래프 데이터 증강을 설계하는데, 그래프 데이터에 앞서 범위와 패턴에 대해 매개 변수화되었다.
(ii) 상관된(correlated) 뷰를 얻기 위해 이를 활용하여 다양한 그래프 구조 데이터에 대해 특수 섭동(perturbations)에 불변하는 표현을 학습할 수 있도록 GNN 사전 훈련을 위한 새로운 그래프 대조 학습 프레임워크(GraphCL)를 제안한다. 또한, 우리는 GraphCL이 실제로 상호 정보 극대화를 수행한다는 것을 보여주며, GraphCL과 최근 제안된 대조 학습 방법 사이의 연관성을 도출하여 그래프 구조 데이터에 대한 광범위한 대조 학습 방법을 통합하는 일반적인 프레임워크로 다시 작성할 수 있음을 보여준다.
(iii) 다양한 유형의 데이터 세트에서 서로 다른 증강의 성능을 평가하기 위해 체계적인 연구가 수행되어 성능의 근거를 밝히고 특정 데이터 세트에 대한 프레임워크를 채택하기 위한 지침을 제공한다.
(iv) 실험에 따르면 GraphCL은 준감독 설정에서 최첨단 성능을 달성한다.교육 학습, 감독되지 않은 표현 학습 및 전이 학습. 또한 일반적인 적대적 공격에 대한 견고성을 향상시킨다.

2 Related Work

Graph data augmentation.

그래프 구조 데이터에 대한 증강은 여전히 충분히 탐구되지 않은 상태로 남아 있으며, 이러한 라인에 따른 일부 작업은 수행되지만 엄청난 추가 계산 비용이 필요하다.

Pre-training GNNs

(self-supervised) 사전 훈련이 컨볼루션 신경망(CNN)에 대한 일반적이고 효과적인 계획이지만 GNN에 대해서는 거의 탐구되지 않는다. 한 가지 예외는 전이 학습 설정에서 사전 훈련 전략을 연구하는 것으로 제한된다. 우리는 사전 훈련된 GNN은 그래프 구조 데이터 소스의 다양한 분야로 인해 전송이 쉽지 않다고 주장한다. 전송 중에 사전 훈련과 다운스트림 작업 모두에 상당한 도메인 지식이 필요하며, 그렇지 않으면 부정적인 전송으로 이어질 수 있다.

Contrastive learning.

대조 학습의 주요 아이디어는 적절한 변환 하에서 표현이 서로 일치하도록 만드는 것으로, 최근 시각적 표현 학습에 대한 관심이 급증하고 있다. 병렬적으로 그래프 데이터의 경우, 정점의 인접 정보를 재구성하려는 전통적인 방법은 구조 정보를 희생하면서 근접 정보를 지나치게 강조하면서 일종의 "국소 대비"(“local contrast")로 취급될 수 있다. 구조 정보를 더 잘 포착하기 위해 로컬 및 글로벌 표현 간의 대조 학습을 수행할 것을 제안함으로써 동기 부여된다. 그러나 그래프 대비 학습은 지금까지와 같이 섭동 불변성을 시행하는 관점에서 탐구되지 않았다.

3 Methodology

3.1 Data Augmentation for Graphs

데이터 증강은 의미론적 레이블에 영향을 미치지 않고 특정 변환을 적용하여 새롭고 현실적으로 합리적인 데이터를 생성하는 것을 목표로 한다. 계산 비용이 비싼 일부를 제외하고 그래프에 대해서는 여전히 충분히 조사되지 않은 상태로 남아 있다(2항 참조). 우리는 그래프 수준의 증강에 초점을 맞춘다. M 그래프의 데이터 세트에서 그래프 G ∈ {Gm : m ∈ M} 이 주어지면, 우리는 G' ~ q(G'|G)를 만족시키는 G'을 공식화한다. 여기서 함수 q(·|G)는 데이터 분포에 대한 인간의 이전 값을 나타내는 사전 정의된 원래 그래프에 조건화된 증강 분포(함수)이다. 예를 들어, 이미지 분류의 경우, 회전 및 자르기 응용 프로그램은 사람들이 회전된 이미지 또는 로컬 패치로부터 동일한 분류 기반 의미 지식을 획득하기 전에 인코딩한다.
그래프에 관해서라면, 같은 개념이 존재할 수 있다. 그러나 1항에 명시된 한 가지 과제는 그래프 데이터 세트가 다양한 분야에서 추상화되기 때문에 이미지에 대한 데이터 확대만큼 보편적으로 적절한 데이터 증강이 없을 수 있다는 것이다. 다시 말해, 다양한 범주의 그래프 데이터 세트에 대해 일부 데이터 증강이 다른 것들보다 더 바람직할 수 있다. 우리는 주로 생화학 분자(예: 화학 화합물, 단백질), 소셜 네트워크 및 이미지 슈퍼 픽셀 그래프의 세 가지 범주에 초점을 맞춘다. 다음으로, 우리는 그래프 구조 데이터에 대한 네 가지 일반적인 데이터 증강을 제안하고 그들이 도입하는 직관적인 사전 사항에 대해 논의한다.

Node dropping.

그래프 G가 주어지면 노드 드롭은 연결과 함께 정점의 특정 부분을 무작위로 폐기한다. 그것에 의해 시행된 근본적인 가정은 정점의 일부가 누락된 것이 G의 의미론적 의미에 영향을 미치지 않는다는 것이다. 각 노드의 드롭 확률은 기본 i.i.d. 균등 분포(또는 다른 분포)를 따른다.

Edge perturbation.

그것은 특정 비율의 모서리를 무작위로 추가하거나 떨어뜨림으로써 G의 연결성을 교란시킬 것이다. 이는 G의 의미적 의미가 에지 연결 패턴 분산에 대한 특정 견고성을 가지고 있음을 암시한다. 우리는 또한 각 에지를 추가/삭제하기 위해 아이디 균일 분포를 따른다.

Attribute masking.

속성 마스킹은 모델이 컨텍스트 정보, 즉 나머지 속성을 사용하여 마스킹된 정점 속성을 복구하도록 촉구한다. 기본 가정은 부분 정점 속성이 누락된 것이 모델 예측에 큰 영향을 미치지 않는다는 것이다.

Subgraph.

이것은 무작위 워크를 사용하여 G의 하위 그래프를 샘플링한다(알고리즘은 부록 A에 요약된다). 그것은 G의 의미론이 그것의 (부분적인) 국소 구조에서 많이 보존될 수 있다고 가정한다. 즉 국소구조에 충분한 정보가 담겨있을 것이라고 가정한다.

The default augmentation (dropping, perturbation, masking and subgraph) ratio is set at 0.2.

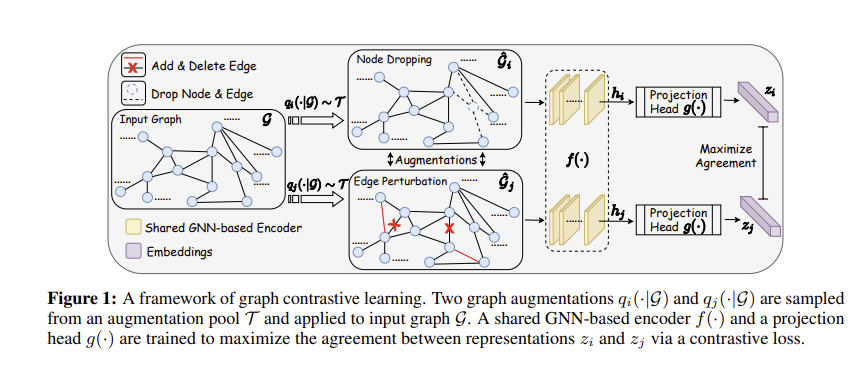
3.2 Graph Contrastive Learning

시각적 표현 학습(2항 참조)의 최근 대조적 학습 발전에 자극을 받아, 우리는 GNN의 (자체 지도) 사전 훈련을 위한 그래프 대조적 학습 프레임워크(GraphCL)를 제안한다. 그래프 대비 학습에서 사전 훈련은 그림 1과 같이 잠재 공간에서 대비 손실을 통해 동일한 그래프의 두 증강 보기 간의 일치를 최대화하는 방식으로 수행된다. 프레임워크는 다음의 4가지 주요 구성 요소로 구성된다.
(1) 그래프 데이터 확대. 주어진 그래프 G는 그래프 데이터 증강을 통해 두 개의 상관 관계 보기 g^i, gˆj를 양의 쌍으로 얻는다. 그래프 데이터 세트의 다양한 도메인에 대해, 데이터 증강을 전략적으로 선택하는 방법이 중요하다고 생각되어진다.
(2) GNN 기반 인코더이다. GNN 기반 인코더 f(·)( (2)에서 정의)는 증강 그래프 gˆi, g^j에 대한 그래프 수준 표현 벡터 hi, hj를 추출한다. 그래프 대비 학습은 모든 GNN 아키텍처에 적용가능하다.
(3) 투사 헤드. 투영 헤드로 명명된 비선형 변환 g(·)는 증강된 표현을 대비 손실이 계산되는 다른 잠재 공간에 매핑한다. 그래프 대비 학습에서 2계층 퍼셉트론(MLP)을 적용하여 zi, zj를 얻는다.
(4) 대비 손실 함수. 대조 손실 함수 L(·)은 음의 쌍과 비교하여 양의 쌍 zi, zj 사이의 일관성을 최대화하기 위해 정의된다. 여기서 normalized temperature-scaled cross entropy loss(NT-Xent)을 활용한다.

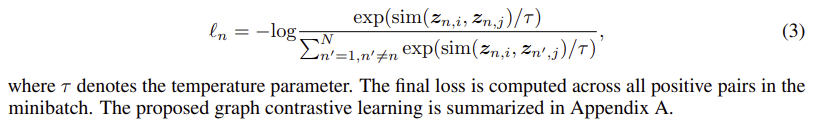
4 The Role of Data Augmentation in Graph Contrastive Learning

이 섹션에서는 GraphCL 프레임워크에서 그래프 구조 데이터에 대한 데이터 증강의 역할을 평가하고 합리화한다. 그림 2에 나타난 바와 같이 다양한 증강 유형 쌍이 세 가지 범주의 그래프 데이터 세트에 적용된다(표 2, 부록 C의 슈퍼 픽셀 그래프에 대한 논의는 남겨 둔다). 실험은 사전 훈련 및 미세 조정 접근법에 따라 준지도 환경에서 수행된다.

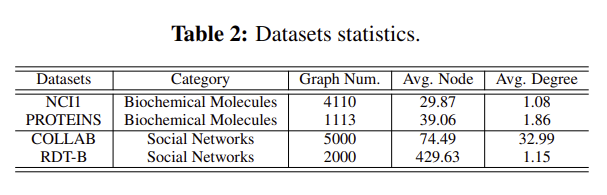
데이터 종류들, 분자2개 소셜2개

4.1 Data Augmentations are Crucial. Composing Augmentations Benefits.

그림 2의 맨 위의 맨 우측 칸을 보면, 이는 identical-identical로 데이터 증강을 하지 않은 경우 이다. 여타 칸들에 비하여 정확도 값이 음수인 것을 확인할 수 있다.

Obs. 1. Data augmentations are crucial in graph contrastive learning.

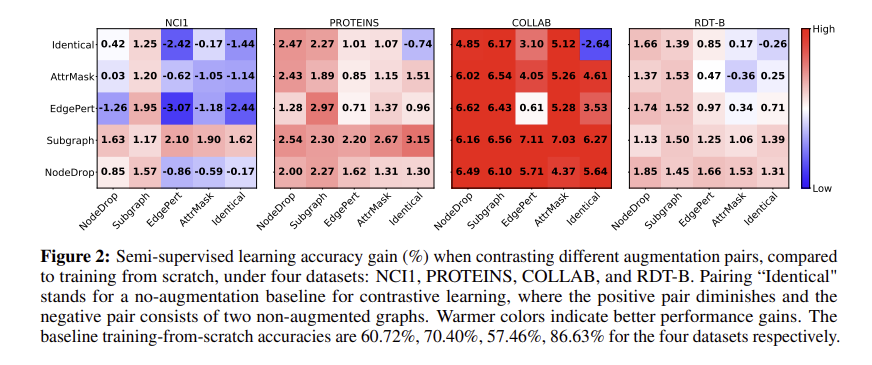
학습과정을 확인하게 된다면 데이터 증강을 거친 2개의 결과를 비교하는데 이것을 각각 쌍별로 확인한 것이다. 대부분 왠만하면 더 좋은 결과가 나타났으며 별다른 하이퍼파라미터 튜닝 없이 진행했는데 이정도이다. 다만 도메인별로 상이한 결과가 나타났다.

Obs. 2. Composing different augmentations benefits more.

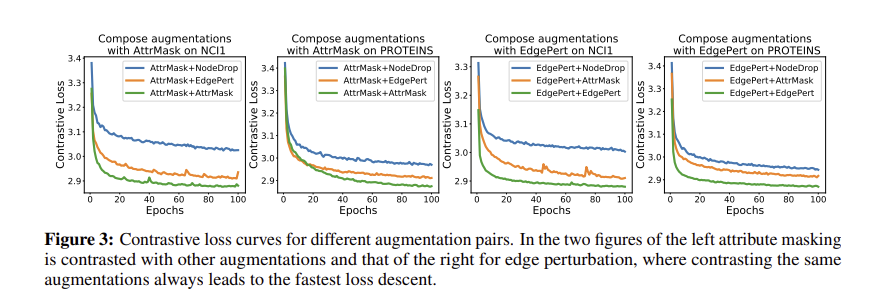
왠만하면 다른 데이터 증강을 이용하는 것이 좋다. 각 데이터셋 별 최고값은 대각 행렬에 존재하지 않다. 아마 그 이유는 같은 데이터 증강을 사용할 경우 shortcut 을 포착하게 되어 overfitting이 되기 때문일 것이다.
그림 3을 보면 같은 어그의 경우 수렴속도가 매우 빠른 것을 확인할 수 있다.

4.2 The Types, the Extent, and the Patterns of Effective Graph Augmentations

이전 그림에서 보았듯이 데이터 세트별로 결과의 차이가 유의미하게 나타나는 것을 확인할 수 있었다. 따라서 데이터 세트, 도메인 별로 가장 유익한 증강세트가 각각 존재할 것이라고 예상한다. 또한 증강의 범위와 패턴에 대한 연구도 진행한다.

Obs. 3. Edge perturbation benefits social networks but hurts some biochemical molecules.

엣지 섭동은 소셜에서는 좋으나, 분자에선 안좋다. 그 이유를 가정한다면 아마 "규칙"이 분자구조에선 더 엄밀히 중요하기 때문이다. 좋은 예로 단순히 분자에서 연결이 생기고 사라지는 것 자체가 화학적인 의미와 더불어 그 성질을 급격하게 변화시키기 때문이다. 맨 왼쪽만 화학데이터 인데 안타까운 성능을 보인다.

Obs. 4. Applying attribute masking achieves better performance in denser graphs.

avg degree가 높았던 collab데이터의 경우 attribute masking의 성능이 다른 것들에 비해 높게 나왔다. 4c 4d비교

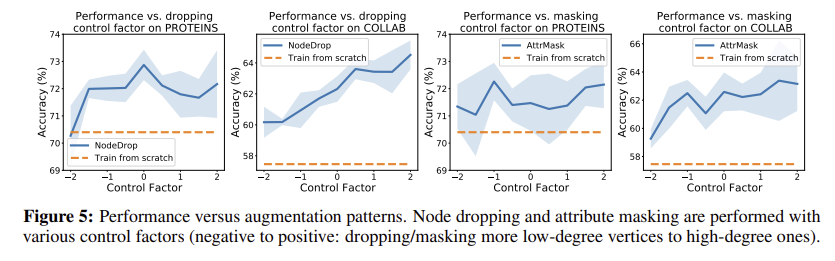
또한 패턴에 대해서도 분석해본다면, masking 률을 늘리면 dense 한 collab의 성능이 더 높아진다. isolate한 것들은 masking시 예측이 힘들지만 dense한 것들은 이런 노드들이 적기 때문일 것이다. 5c,5d

Obs. 5. Node dropping and subgraph are generally beneficial across datasets.

4.3 Unlike “Harder” Ones, Overly Simple Contrastive Tasks Do Not Help.

옵스 2에서 논의한 바와 같이, "더 어려운" 대조 학습은 다른 유형의 증강을 구성함으로써 "더 어려운" 과제가 달성되는 경우 더 많은 이익을 얻을 수 있다. 이 섹션에서는 매개 변수화된 증강 강도/패턴과의 관계에서 정량화할 수 있는 난이도를 추가로 탐색하고 난이도가 성능 향상에 미치는 영향을 평가한다.직관적으로, 드롭/마스크 비율 또는 제어 계수α가 클수록 대조 작업이 어려워지며, 이는 고려된 범위에서 더 나은 협업 성능(그림 4 및 5)을 낳았다. 지나치게 간단한 작업에 해당하는 매우 작은 비율 또는 음의 α도 난이도를 증가시키는 하위 그래프 변형을 설계하고 유사한 결론에 도달한다.

Summary.

전체적으로, 우리는 섹션 5에 대한 증강 풀을 다음과 같이 결정한다. 생화학 분자에 대한 노드 드롭 및 하위 그래프, 밀도 높은 소셜 네트워크에 대한 노드 드롭 및 하위 그래프, 그리고 희소 소셜 네트워크에 대한 속성 마스킹을 제외한 모든 것이다. 강점이나 패턴을 바꾸면 더 많은 도움이 될 수 있다.

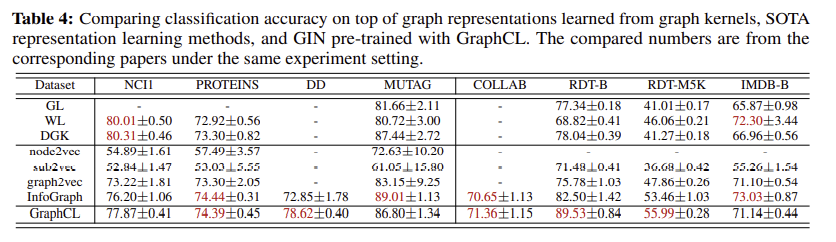
5 Comparison with the State-of-the-art Methods

self-supervised

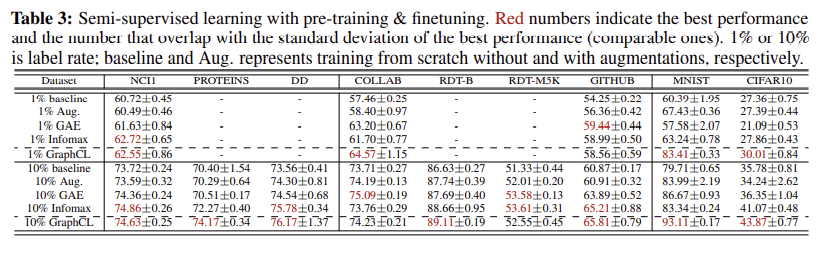
unsupervised

a down-stream SVM classifier
MUTAG and IMDB-B consists of graphs with average node number less than 20).

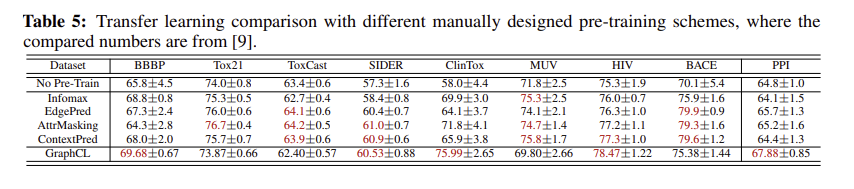
transferring

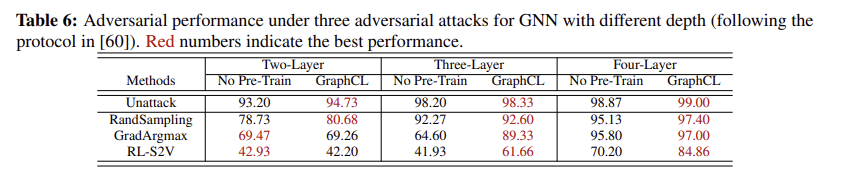
Adversarial robustness

6 Conclusion

본 논문에서는 그래프 구조 데이터의 고유한 과제에 직면하여 GNN 사전 훈련을 위한 대조 학습을 탐구하기 위해 명시적인 연구를 수행한다. 첫째, 데이터 배포에 앞서 특정 인간을 도입하는 것에 대한 각 논의와 함께 몇 가지 그래프 데이터 증강이 제안된다. 새로운 증강과 함께, 우리는 엄격한 이론적 분석과 함께 불변 표현 학습을 용이하게 하기 위해 GNN 사전 훈련을 위한 새로운 그래프 대조 학습 프레임워크(GraphCL)를 제안한다. 우리는 제안된 프레임워크에서 데이터 증강의 영향을 체계적으로 평가하고 분석하여 근거를 밝히고 증강 선택을 안내한다. 실험 결과는 일반화 가능성과 견고성 모두에서 제안된 프레임워크의 최첨단 성능을 검증한다.