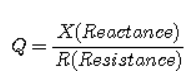L과 C 이해하기

• L과 C는 정반대의 특성과 현상을 보임

1. L: 인덕턴스, 유도용량

• 회로를 흐르고 있는 전류의 변화에 의해 전자기유도로 생기는 역기전력의 비율
• RF에선 nH 단위가 주로 사용됨
• 코일 : 인덕턴스는 선로 길이가 길 때 나타나는 현상 → 선로를 스프링 모양으로 감으면 적은 면적 상에 많은 인덕턴스 구현 가능
  - 상호 인덕턴스가 강해져 신로 길이보다 더 많은 인덕턴스를 구현할 수 있음
  • 주로 저주파에서 사용되는 용어, 고주파에서는 이런 코일 구조 뿐 아니라 다양한 구조가 응용됨

2. C : 캐패시턴스, 정전용량

• 전압을 가했을 때 축적되는 전하량의 비율
• 주로 pF 단위

RF에서의 L과 C의 의미 정확히 이해하기

L과 C의 주파수 특성

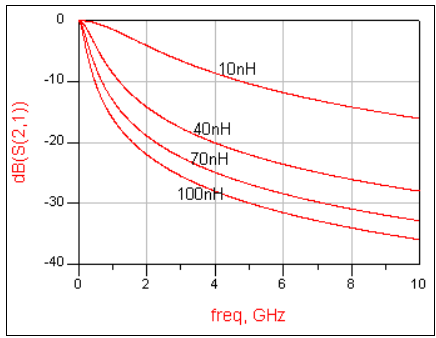
인덕터의 S파라미터 특성

• 주파수가 높아질수록 잘 통과하지 못 함
• L값이 높아질수록 더더욱 통과하지 못함
  

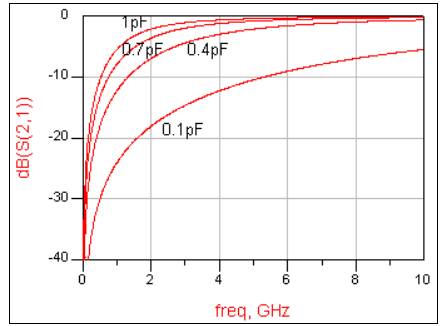
캐패시터의 s파라미터

• 인덕터와는 정반대로 주파수가 낮을수록 잘 통과하지 못 함
• C값이 높아질수록 저주파는 물론 고주파 성분이 더 많이 통과
  

정리

1. L(인덕턴스) : 주파수가 올라갈수록 얼마나 고주파의 흐름을 방해하는가?
2. C(캐패시턴스) : 주파수가 올라갈수록 얼마나 고주파의 흐름을 원활하게 하는가?

L : 인덕턴스

• 도선에 전류가 흐를 때 그 전류의 변화를 막으려는 성질 또는 그 정도
• 일종의 전기적 관성
  ⇒ 전류/전압파형의 크기, 방향이 주기적으로 변하는 교류가 입력되면 그 변화를 막음
  ⇒ DC는 잘 통과, AC는 통과 어렵
• 인덕턴스는 길이를 가지는 모든 선로에서 발생
  
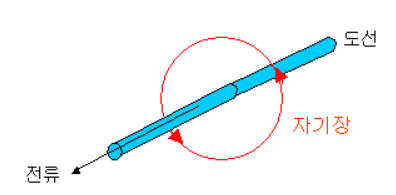
• 아무 선로건 그 선로 길이 방향으로 둥글게 자기장을 형성하게 되는데, 만약 이 선로를 따라 흐르던 전류가 변화하려 하면 그 주변에 생성된 자기장도 같이 바뀌여야만 함. 바로 이렇게 선로 주위에 생성된 자기장이 선로의 전류/전압 변화를 따라가려면 어느정도 시간이 필요해짐. 결국 도선의 전류 변화를 방해하는 꼴
• 그리고 이러한 주변의 자기장이 많이 생길수록 (즉 L값이 커질수록) 전류가 변화하기가 무척 힘들어짐
• 따라서 L값이 높을수록 고주파는 통과하기 힘들어짐
• 인덕터는 선로를 길게 만들면 됨 (코일 형태가 대표적)
• 코일 형태로 만들어 놓으면 실제 그 선로 길이만으로 구현한 것보다 L값을 증가시킬 수도 있음 (self inductance(자기 유도), mutual inductance(상호 유도))
  
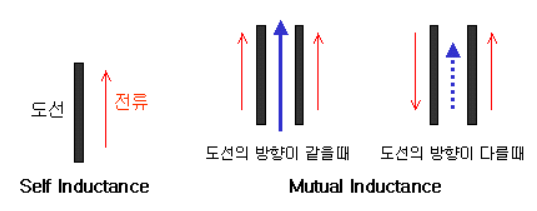
• 전류가 같은 방향이라면 상호간의 주변의 자기장이 서로 더해져 L값이 더욱 세짐
• 전류가 서로 다르게 흐르고 있다면 서로 간의 자기장 방향이 달라 상쇄가 되기 때문에 전체적인 L값이 작아짐
• Microstrip과 같이 패턴을 통해 인덕터를 구현하려면 선로를 길게 만들어야하는데 공간적 제약 때문에 아래와 같은 세가지의 inductor 형태를 주로 이용
  
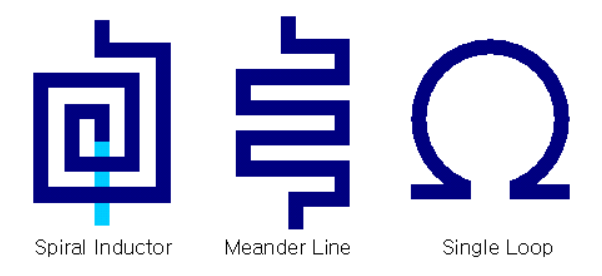
• 가장 많이 이용되는건 Spiral Inductor
  - 한 방향으로 동심원을 그리기 때문에 mutual inductance에서 같은 방향으로 자기장이 더해져 작은 크기로 큰 L값을 만들 수 있음
  • loss가 심함
  • 중앙부에서 다른쪽으로 연결해야하기 때문에 반드시 air bridge나 다층 선로를 이용해야함
• meander line : air bridge가 필요없도록 그냥 뱀처럼 꼬아놓은 것
  - mutual inductance가 반대로 일어남. 서로 상쇄되어 크기에 비해 그다지 높은 L값을 만들기 힘들다는 단점

C : 캐패시턴스

• 단절된 금속 사이에서 전류/전압의 변화가 있을 때만 신호를 통과시키려는 성질
  
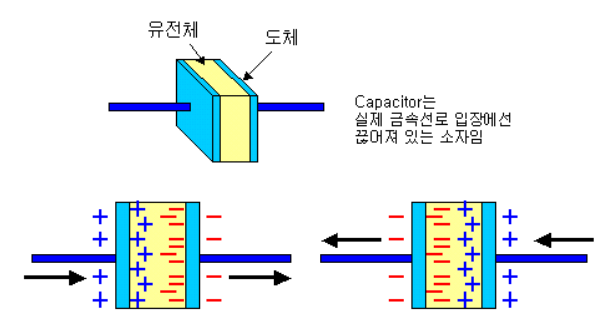
• 교류의 경우에는 한쪽에 전극이 형성되면 유전체 내에서도 전극이 쏠리면서 분극되고, 그 결과 상대쪽 금속판에도 반대의 전극을 형성시켜 줄 수 있게 됨. 그리고 그것이 주기적으로 변하면 건너편 금속의 전극이나 전압도 주기적으로 변화시켜 주게 되어 결국 끊어진 금속판 사이로 교류파형의 변화 형상, 즉 신호가 전달되게 됨.
• 직류에 있어서는 처음 전압이 인가된 순간에만 유전체가 분극을 일으키고는 이내 사라지기 때문에 전기적 신호 전달이 불가능

스미스차트에서의 L과 C

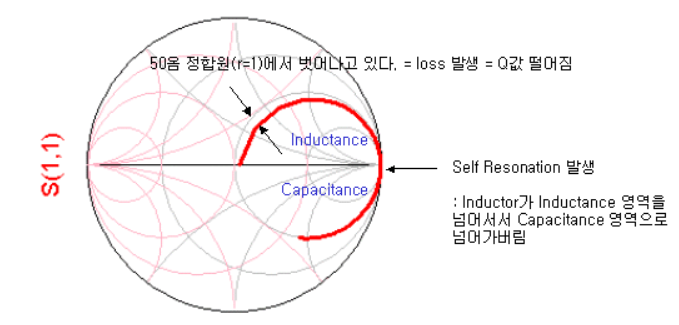
• 입출력단에 50옴 포트를 인가한 pass through 상태에서의 S11
  
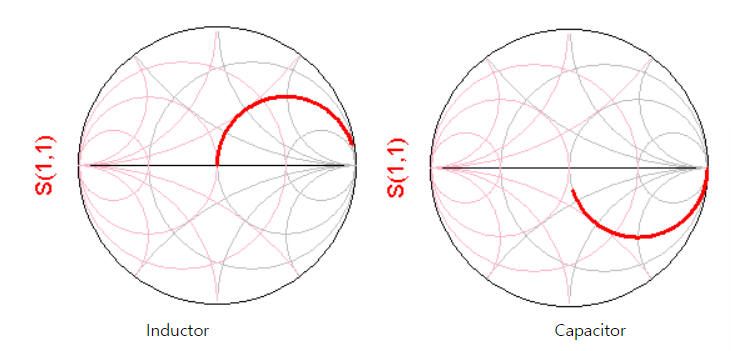
• 스미스 차트 원의 위쪽은 임피던스 허수부가 +일때, 아래쪽은 임피던스 허수부가 -일 때
• 인덕터가 오른쪽 R=1 인 원 상에 올라가 있다는 것은 R값이 matching된, 즉 손실이 없는 상태를 의미

공진(Resonance)

• 특정 주파수에 에너지가 집중되어, 해당 주파수만 골라내거나 걸러내는 주파수 선택 특성이 나타나는 것
• 에너지 관점에서 볼 때 L 성분과 C성분이 동시에 공존하면서 평형상태를 이루고 있는 지점
  

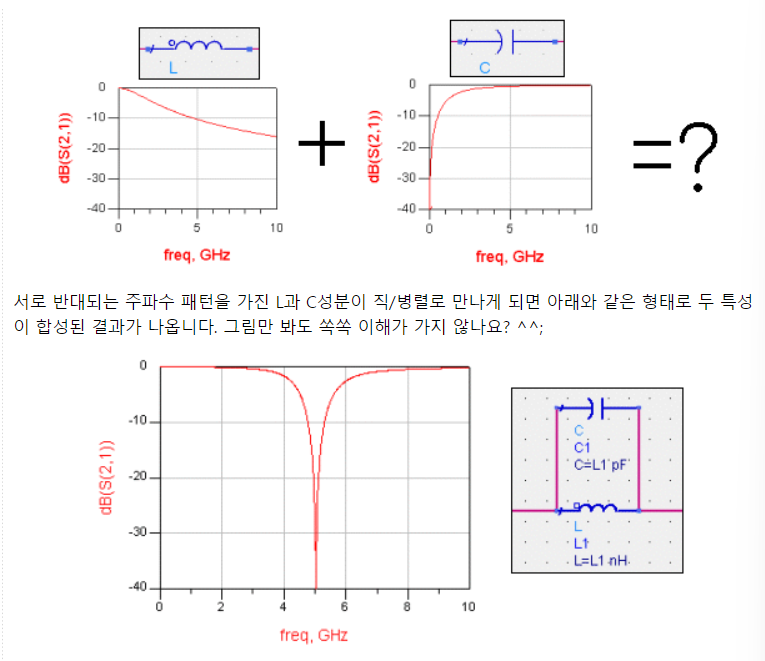
필터에서의 L과 C

1. LPF
   
2. HPF
   L과 C의 소자 위치를 정반대로 바꾼 것
   ★ inductor, capacitor 소자 같은 lumped element로만 만드는 것이 아니라 어떤 구조든 inductance와 capacitance를 유발할 수 있다면 그것들을 조합하여 다 filter로 만들 수 있음

SRF(self resonating frequency)

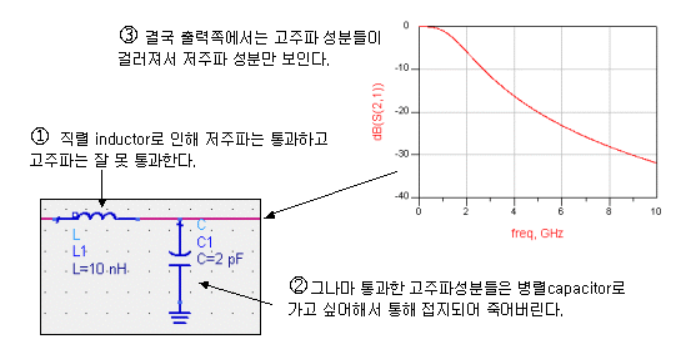
• 아래는 실제 인덕터의 S21를 나타낸 그림
  
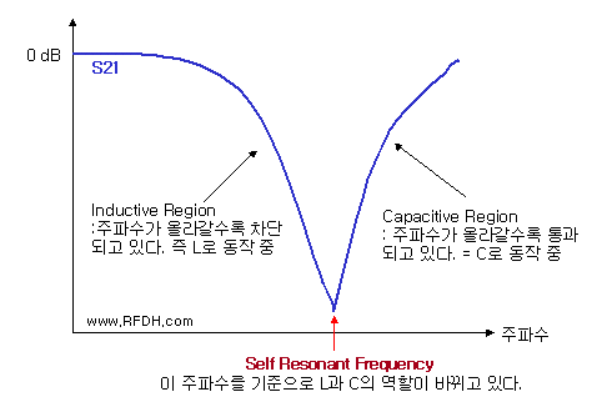
• inductor건 capacitor건 특정 주파수를 넘어버리면 자신의 역할이 반대로 뒤집어짐
• 이렇게 역할이 깨져버리는 주파수점이 마치 공진점과 같기 때문에 self resonating frequency라 불림
• 따라서 모든 인덕터, 캐패시터를 사용할 때는 반드시 SRF보다 어느정도 낮은 주파수에서 사용해야함
• 아래는 실제 소자의 인덕터와 캐패시터의 S파라미터 그래프를 보여줌
  
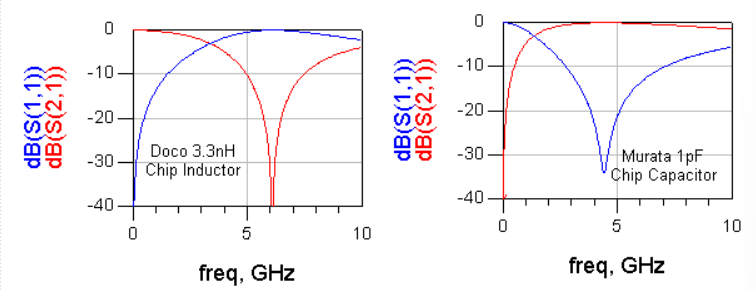
• 왜 실제상에서 이런 일이 발생?(Sprial Inductor)
  
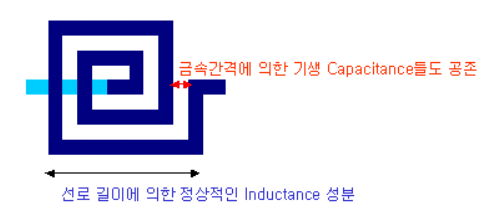
• 주파수가 올라가면 기생 cap의 영향으로 인덕터가 캐패시터로 역할이 바뀌게 됨
• 소자값이 커질수록 실제 소자의 물리적 구조도 커지기 때문에 덩달아 기생성분도 더 커져서 결국 SRF는 점점 작아짐. 즉, 쓸 수 있는 주파수 영역이 좁아짐
• lumped element의 경우 SRF가 수 GHz 대밖에 안돼서 그 이하의 주파수에서만 사용해야함. 따라서 아주 높은 주파수에서는 lumped element를 사용하지 못 하게 되고, 그래서 microstrip과 같은 분산소자로서 L,C를 구현할 필요가 생김

인덕터와 캐패시터의 Q(quality factor)

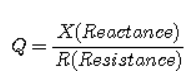
• 임피던싀의 허수부/실수부
• 소자의 loss가 얼마냐
• 리액턴스 X는 L과 C과 같은 무손실성 저장성분
  - 전기장 혹은 자기장의 형태로 주파수 별로 에너지를 축적하는 기능
• R은 저항값, 저항에 의한 손실을 의미
• L과 C에도 작은 저항이 있음. 따라서 L 또는 C값을 이런 기생저항값으로 나눈 값을 Q(quality factor)
• 이러한 Q값은 주파수에 따라 다르며, 또한 소자값에 따라 다름
• Q값이 클수록 loss가 적음
  

RF에서의 L과 C