[알고리즘] Heap Sort

Abstract

• 완전 이진 트리(Complete binary tree)를 기본으로 하는 힙(Heap) 자료구조를 기반으로 한 정렬 방식

Complete binary tree
삽입 시 왼쪽부터 차례대로 추가하는 이진 트리

Heap
큰 키(우선 순위)에 자주 엑세스 하거나 키(우선 순위) 중심으로 정렬된 시퀀스를 활용해야 할 때 유용한 자료구조이다.

Heap property

heap order property

각 노드의 값은 자신의 자식노드가 가진 값보다 크거나 같다. Max heap
각 노드의 값은 자신의 자식노드가 가진 값보다 작거나 같다. Min heap

heap shape property

완전 이진 트리 모양으로, 마지막 레벨의 모든 노드는 왼쪽에 쏠려 있다.

Process(Ascending)

1. 주어진 원소들로 최대 힙을 구성한다.
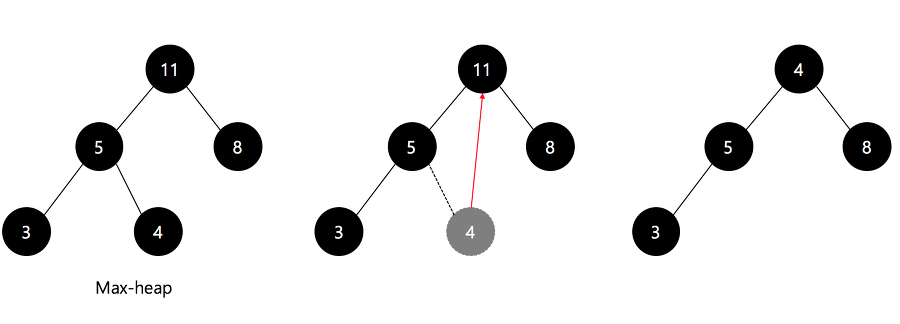
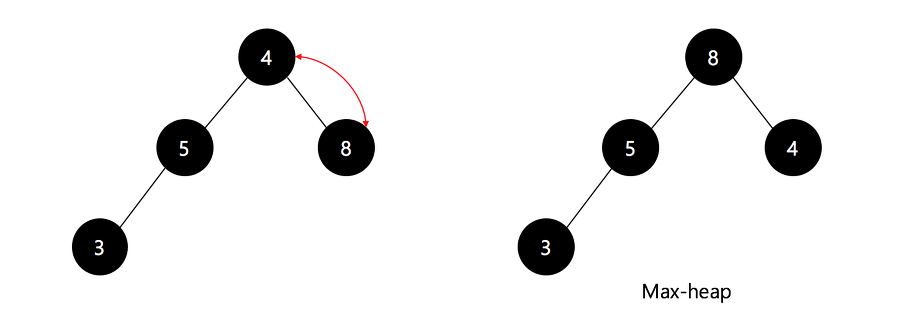
2. 최대 힙의 루트노드와 말단노드를 교환하고 말단노드를 꺼낸다.
   루트노드 현재 배열의 첫번째 요소 ➡ 최댓값
   말단노드 현재 배열의 마지막 요소
   
3. 새 루트노드에 대해 최대 힙을 구성한다.
   
4. 원소의 개수만큼 2번과 3번을 반복 수행한다.

C++ Code(Ascending)

HeapSort

void heapSort(int arr[], int arrSize){
  int n = arrSize;

  // Build Max Heap : 1단계
  for(int i=n/2-1; i>=0; i--){
    heapify(arr, n, i);
  }

  // 힙 크기를 줄이고 자리 이동 : 2~4단계
  for (int i=n-1; i>0; i--){
    swap(arr[0], arr[i]);
    heapify(arr, i, 0);
  }
}

Heapify

주어진 자료구조에서 힙 성질을 만족하도록 하는 연산

void heapify(int arr[], int n, int i){
  int p = i;
  int l = i*2 + 1;
  int r = i*2 + 2;

  // 왼쪽 자식 노드
  if (l < n && arr[p] < arr[l]){
    p = l;
  }
  // 오른쪽 자식 노드
  if (r < n && arr[p] < arr[r]){
    p = r;
  }

  // 부모노드 < 자식노드
  if(i != p){
    swap(arr[p], arr[i]);
    heapify(arr, n, p);
  }
}

GIF로 이해하는 Heap Sort

시간복잡도

• Heapify : log₂n
  말단 노드(최댓값)이 루트 노드에 올라오기까지 트리의 높이만큼 자리를 이동해야 하므로 log₂n 만큼 이동해야 한다.

• Heapify를 해야 하는 노드 개수 : n

따라서 시간복잡도는 Heapify * Heapify를 해야 하는 노드 개수 = nlog₂n가 된다.

Best case : O(nlog₂n)
Worst case : O(nlog₂n)
Average case : O(nlog₂n)

공간복잡도

O(n)

장점

• 가장 크거나 작은 값을 구할 때 최소 힙, 최대 힙의 루트 값이기 때문에 한 번의 힙 구성으로 값을 구할 수 있다.
• 최대 k만큼 떨어진 요소들을 정렬할 때, 삽입 정렬보다 더욱 개선된 결과를 얻을 수 있다.

단점

• 불안정 정렬(Unstable Sort)이다.

참고 사이트

Heap Sort1
Heap Sort2
최대 힙과 최소 힙
Heap Sort Image